Оглавление:
Статистическая оценка — это статистика, которая используется для оценивания неизвестных параметров распределений случайной величины.
Выборки и выборочные характеристики
Рассмотрим эксперимент 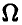 , описание которого строится при помощи случайной величины
, описание которого строится при помощи случайной величины 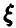 , или, что то же самое, рассмотрим случайную величину
, или, что то же самое, рассмотрим случайную величину 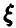 , которую мы можем наблюдать в эксперименте
, которую мы можем наблюдать в эксперименте 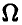 . Это означает, что однократный эксперимент
. Это означает, что однократный эксперимент 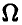 дает нам возможность определить одно из возможных значений случайной величины
дает нам возможность определить одно из возможных значений случайной величины 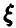 .
.
Пусть в результате n экспериментов П получен набор значений случайной величины 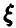

Если случайная величина 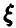 в процессе экспериментирования не менялась, если не менялись условия проведения эксперимента
в процессе экспериментирования не менялась, если не менялись условия проведения эксперимента 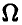 и все измерения значений случайной величины
и все измерения значений случайной величины 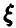 проводились независимо друг от друга, то говорят, что набор (1) образует выборку объема n из распределения случайной величины
проводились независимо друг от друга, то говорят, что набор (1) образует выборку объема n из распределения случайной величины 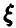 .
.
Заметим, что если сказано: некоторая совокупность из n чисел образует выборку, то при этом предполагается следующее:
а) эксперимент 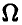 может быть проведен при неизменных условиях сколько угодно раз;
может быть проведен при неизменных условиях сколько угодно раз;
б) имеет место устойчивость частот, т. е. имеет смысл говорить о вероятности попадания вектора 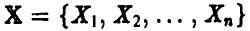 в некоторое наперед заданное множество А из множества всех возможных совокупностей (1) (обычно
в некоторое наперед заданное множество А из множества всех возможных совокупностей (1) (обычно 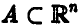 ).
).
Предположение а) означает, что, говоря о выборке объема n, мы говорим не о n конкретных числах, а о целой матрице чисел

где элемент 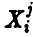 — это значение случайной величины
— это значение случайной величины 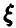 , полученное в i-м эксперименте
, полученное в i-м эксперименте 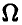 , который проводился в j-й серии,
, который проводился в j-й серии, 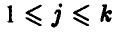 . Таким образом, можно дать следующее (уточняющее) определение выборки: выборкой объема n из закона распределения случайной величины
. Таким образом, можно дать следующее (уточняющее) определение выборки: выборкой объема n из закона распределения случайной величины 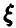 называется совокупность n штук независимых одинаково распределенных случайных величин, совпадающих с
называется совокупность n штук независимых одинаково распределенных случайных величин, совпадающих с 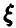 .
.
Пример:
Измеряется n однотипных деталей, изготовленных на одном станке. В результате получена совокупность чисел 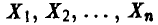 , которые образуют выборку из распределения случайной величины
, которые образуют выборку из распределения случайной величины 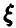 — размер изготовляемой на данном станке детали.
— размер изготовляемой на данном станке детали.
Пример:
Измеряется п однотипных деталей, изготовленных на различных станках. Получается совокупность чисел 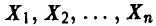 . Эти числа, вообще говоря, выборку не образуют, так как может, например, оказаться, что точность изготовления детали на различных станках различна и, следовательно, числа
. Эти числа, вообще говоря, выборку не образуют, так как может, например, оказаться, что точность изготовления детали на различных станках различна и, следовательно, числа 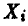 являются реализациями различных случайных величин.
являются реализациями различных случайных величин.
Отметим некоторую неоднозначность термина «выборка». Иногда под выборкой объема n понимают и конкретный набор n чисел, полученных в результате серии из n экспериментов. Но обычно бывает ясно, в каком смысле говорится о выборке. Скажем, если найдено среднее арифметическое по выборке и оно равно 5,
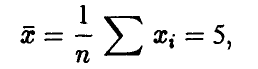
то здесь под выборкой понимается конкретный набор чисел. Если же обсуждаются свойства величины
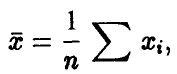
то под выборкой понимается любой возможный набор значений случайной величины 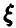 , т. е. совокупность n штук независимых случайных величин.
, т. е. совокупность n штук независимых случайных величин.
Первой статистической задачей, которую мы рассмотрим, будет задача нахождения функции распределения и числовых характеристик случайной величины 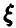 по выборке, полученной в результате эксперимента.
по выборке, полученной в результате эксперимента.
Пусть дана выборка (1) из закона распределения 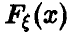 случайной величины
случайной величины 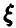 . Требуется определить функцию распределения
. Требуется определить функцию распределения 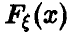 случайной величины
случайной величины 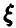 и ее моменты.
и ее моменты.
Рассмотрим дискретную случайную величину 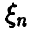 , принимающую значения
, принимающую значения 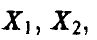
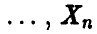 , каждое с вероятностью 1/n.
, каждое с вероятностью 1/n.
Эмпирической функцией распределения случайной величины 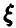 называется функция распределения случайной величины
называется функция распределения случайной величины 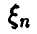
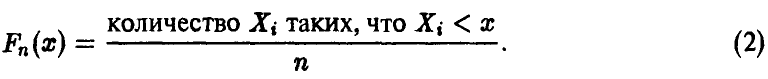
Эмпирическая (или выборочная) функция распределения является случайной величиной, так как она определяется по выборке (1) и зависит от того, какой конкретно набор чисел получен в данной серии из n экспериментов  . Оказывается, что если последовательность
. Оказывается, что если последовательность 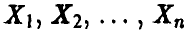 достаточно длинная, то эмпирическая функция распределения будет очень похожей на теоретическую функцию
достаточно длинная, то эмпирическая функция распределения будет очень похожей на теоретическую функцию 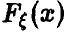 для большинства из возможных наборов чисел
для большинства из возможных наборов чисел 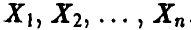 . Точнее, имеет место
. Точнее, имеет место
Теорема Гливенко—Кантелли:
Пусть 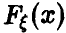 — теоретическая функция распределения случайной величины
— теоретическая функция распределения случайной величины 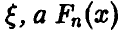 — эмпирическая. Тогда для произвольного значения
— эмпирическая. Тогда для произвольного значения 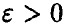
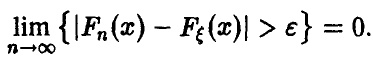
◄ Фиксируем некоторое число х и рассмотрим случайные величины
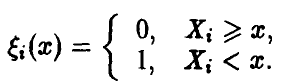
Заметим, что ряд распределения случайных величин 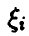 имеет вид
имеет вид
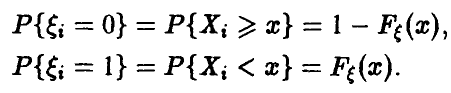
Все 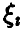 — одинаково распределенные случайные величины с указанным рядом распределения и конечным математическим ожиданием
— одинаково распределенные случайные величины с указанным рядом распределения и конечным математическим ожиданием
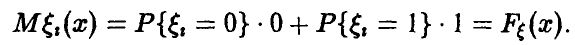
Применяя к последовательности случайных величин £(х) закон больших чисел в форме Хинчина, получаем
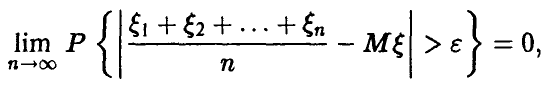
откуда следует утверждение теоремы. ►
Теорема позволяет сделать вывод: эмпирическая функция распределения, построенная по выборке объема n, тем более похожа на 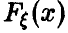 , чем больше n — объем выборки.
, чем больше n — объем выборки.
Этот вывод не является достоверным, а, как утверждает теорема, носит вероятностный характер — вероятность отклонений 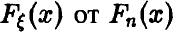 при
при  очень мала — как бы ни была велика выборка, всегда существует возможность получить
очень мала — как бы ни была велика выборка, всегда существует возможность получить 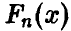 , значительно отличающуюся от
, значительно отличающуюся от 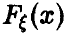 . Однако при достаточно больших п этой возможностью можно пренебречь. Обратимся к поясняющему примеру.
. Однако при достаточно больших п этой возможностью можно пренебречь. Обратимся к поясняющему примеру.
Пример:
Рассмотрим массовое производство некоторых однотипных изделий, изготавливаемых в неизменных условиях. Пусть случайная величина 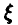 принимает значение 1, если изготовленное изделий доброкачественно, и 0 в противном случае. Отобрано n изделий и среди них оказалось
принимает значение 1, если изготовленное изделий доброкачественно, и 0 в противном случае. Отобрано n изделий и среди них оказалось 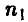 дефектных. Оценить функцию распределения случайной величины
дефектных. Оценить функцию распределения случайной величины 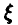 .
.
◄ Случайная величина 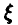 дискретна и задача оценки ее функции распределения есть попросту задача оценки вероятности
дискретна и задача оценки ее функции распределения есть попросту задача оценки вероятности 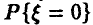 , т. е. вероятности получить дефектное изделие. Теорема Гливенко— Кантелли в этом случае говорит, что оценкой вероятности
, т. е. вероятности получить дефектное изделие. Теорема Гливенко— Кантелли в этом случае говорит, что оценкой вероятности 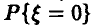 может служить частота появления дефектных изделий в рассматриваемой выборке
может служить частота появления дефектных изделий в рассматриваемой выборке
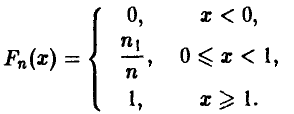
Совершенно ясно, что если нам попалась «хорошая» выборка (которая содержит такой же процент брака, как и вся контролируемая партия), то заменяя неизвестную вероятность 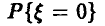 частотой
частотой 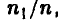 мы ошибемся мало. Если получена «плохая» выборка, то при подобной замене можно допустить ошибку. Однако «плохие» выборки будут попадаться тем реже, чем больше объем рассматриваемой выборки и, следовательно, ошибаться мы также будем редко. Пусть n — 10,
мы ошибемся мало. Если получена «плохая» выборка, то при подобной замене можно допустить ошибку. Однако «плохие» выборки будут попадаться тем реже, чем больше объем рассматриваемой выборки и, следовательно, ошибаться мы также будем редко. Пусть n — 10, 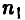 = 2 и истинная вероятность
= 2 и истинная вероятность 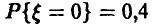 Мы же, изучая нашу выборку, положим
Мы же, изучая нашу выборку, положим 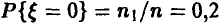 . Вероятность встретить выборку, давшую основание для подобной оценки, будет
. Вероятность встретить выборку, давшую основание для подобной оценки, будет
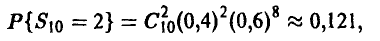
т. е. примерно 12 выборок из 100 в данной ситуации будут плохими Если же заключение о том, что Р = 0,2, мы сделали по выборке n = 25,  = 5, то вероятность встретить плохую выборку
= 5, то вероятность встретить плохую выборку
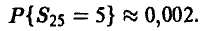
Для выборки n = 100,  = 20 эта вероятность
= 20 эта вероятность
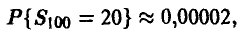
т. е. лишь в двух случаях из 100 000 мы получаем в эксперименте выборку, дающую основание для ложной оценки искомой вероятности. ►
Поскольку вся информация о случайной величине 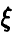 может быть получена при изучении ее функции распределения, а функции распределения случайных величин
может быть получена при изучении ее функции распределения, а функции распределения случайных величин 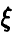 и
и 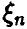 оказались похожи, то следует ожидать, что аналогичная картина будет иметь место и для прочих характеристик случайной величины
оказались похожи, то следует ожидать, что аналогичная картина будет иметь место и для прочих характеристик случайной величины 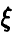 . Таким образом, наблюдаемая в эксперименте случайная величина
. Таким образом, наблюдаемая в эксперименте случайная величина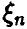 служит своего рода «тенью» изучаемой случайной величины
служит своего рода «тенью» изучаемой случайной величины 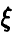 . В дальнейшем мы будем называть ее эмпирическим, или выборочным, аналогом случайной величины
. В дальнейшем мы будем называть ее эмпирическим, или выборочным, аналогом случайной величины 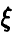 , а все характеристики величины
, а все характеристики величины 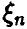 будем именовать эмпирическими, или выборочными, характеристиками случайной величины
будем именовать эмпирическими, или выборочными, характеристиками случайной величины 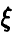 . Так функция распределения случайной величины
. Так функция распределения случайной величины 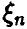 называется эмпирической (выборочной) функцией распределения случайной величины
называется эмпирической (выборочной) функцией распределения случайной величины 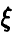 , математическое ожидание
, математическое ожидание 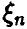 — эмпирическим математическим ожиданием
— эмпирическим математическим ожиданием 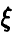 , дисперсия
, дисперсия 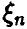 — эмпирической дисперсией
— эмпирической дисперсией 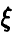 и вообще: эмпирическими (выборочными) моментами случайной величины
и вообще: эмпирическими (выборочными) моментами случайной величины 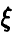 будем называть соответственно моменты случайной величины
будем называть соответственно моменты случайной величины 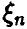 .
.
Эмпирические моменты будем обозначать той же буквой, что и соответствующие теоретические с добавлением вверху звездочки. Тогда эмпирические начальные моменты случайной величины 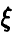 определяются формулой
определяются формулой
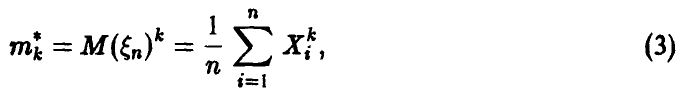
а эмпирические центральные моменты —
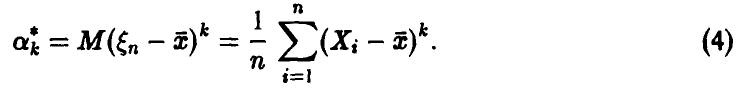
Для первого эмпирического начального момента (среднего значения) обычно используется обозначение

а для второго эмпирического центрального момента и среднеквадратичного отклонения обычно используют обозначения
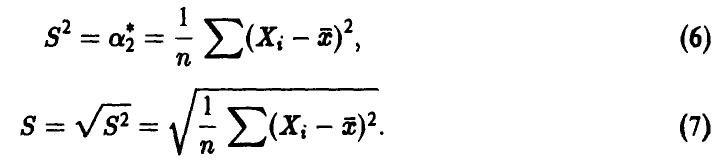
Ими мы и будем пользоваться в дальнейшем.
Имеют место следующие утверждения.
Теорема:
Если n достаточно велико, то начальные эмпирические моменты мало отличаются от соответствующих теоретических, точнее
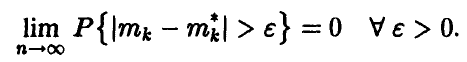
◄ Пусть k — фиксировано. Рассмотрим последовательность случайных величин
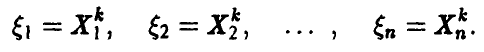
Поскольку все 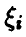 — одинаковые независимые случайные величины, совпадающие со случайной величиной
— одинаковые независимые случайные величины, совпадающие со случайной величиной 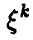 , то
, то
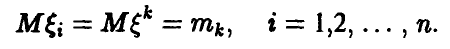
Отсюда и из соотношения (3) следует равенство
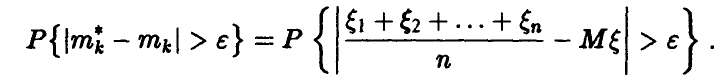
Применяя к последовательности случайных величин 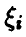 закон больших чисел в форме Хинчина, получаем, что
закон больших чисел в форме Хинчина, получаем, что
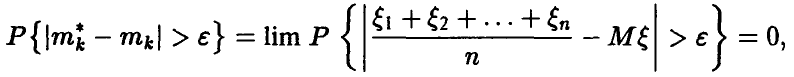
что и требовалось. ►
В теореме, конечно, предполагается, что соответствующие теоретические моменты существуют.
Столь же легко может быть доказана и теорема о близости эмпирических центральных моментов к соответствующим теоретическим.
Теорема:
Если n достаточно велико, то центральные эмпирические моменты мало отличаются от соответствующих теоретических, точнее
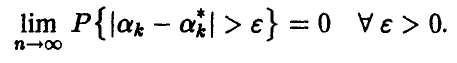
Пусть теперь в эксперименте наблюдается несколько случайных величин (случайный вектор) , 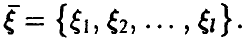
Выборкой объема n из закона распределения случайного вектора 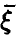 будем называть n реализаций (измерений) случайной величины
будем называть n реализаций (измерений) случайной величины 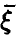
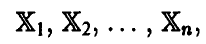
полученных в n независимых экспериментах.
Как и для случая одномерной случайной величины, выборка — это n штук независимых одинаково распределенных векторов. Отметим, что реализацией случайного вектора будет упорядоченный набор l чисел
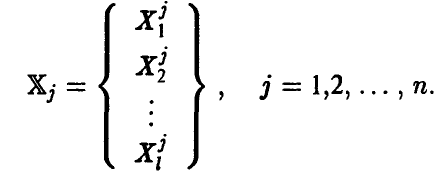
Известно, что важной характеристикой векторной случайной величины является ее ковариационная матрица
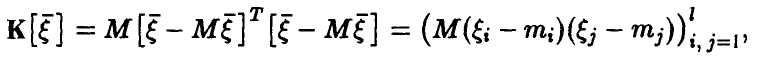
элементы которой — ковариации компонент 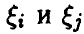 . Ее эмпирический аналог (т. е. ковариационная матрица выборочного вектора
. Ее эмпирический аналог (т. е. ковариационная матрица выборочного вектора 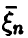 , принимающего значение
, принимающего значение 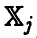 с вероятностью 1/n) называется эмпирической ковариационной матрицей вектора
с вероятностью 1/n) называется эмпирической ковариационной матрицей вектора 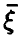
Как следует из вышеизложенного, ее компоненты могут быть найдены по формулам
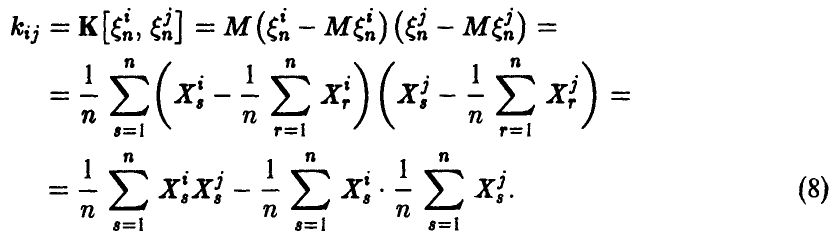
В частности, из соотношения (8) с учетом выражения для эмпирического среднеквадратичного отклонения (7) получаем соотношение для расчета эмпирического коэффициента корреляции пары случайных величин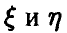
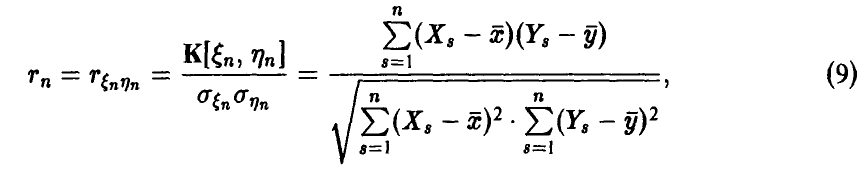
здесь 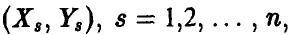 — выборка из двумерного распределения случайных величин
— выборка из двумерного распределения случайных величин 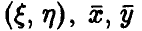 — эмпирические средние случайных величин
— эмпирические средние случайных величин 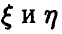 соответственно. Соотношение (9) может быть переписано в эквивалентной форме
соответственно. Соотношение (9) может быть переписано в эквивалентной форме
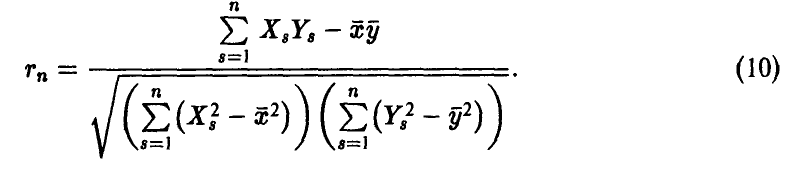
Как и выше, можно доказать теоремы о близости в подавляющем большинстве случаев эмпирических характеристик многомерной случайной величины к соответствующим характеристикам вектора 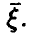 Эти теоремы позволяют высказать более или менее правдоподобное суждение о числовых характеристиках случайной величины
Эти теоремы позволяют высказать более или менее правдоподобное суждение о числовых характеристиках случайной величины 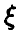 по выборке (1). Конечно, заменяя истинные числовых характеристики эмпирическими, можно ошибиться. Однако, как и в случае с функцией распределения, мы хотим надеяться, что «плохие» выборки будут встречаться редко и что в подавляющем большинстве случаев эмпирические моменты будут мало отличаться от теоретических. Хотелось бы научиться оценивать достоверность наших суждений о рассмотренных выше характеристиках случайной величины
по выборке (1). Конечно, заменяя истинные числовых характеристики эмпирическими, можно ошибиться. Однако, как и в случае с функцией распределения, мы хотим надеяться, что «плохие» выборки будут встречаться редко и что в подавляющем большинстве случаев эмпирические моменты будут мало отличаться от теоретических. Хотелось бы научиться оценивать достоверность наших суждений о рассмотренных выше характеристиках случайной величины 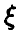 поточнее. Этим мы займемся позднее, а сейчас попробуем несколько расширить наши представления о случайной величине
поточнее. Этим мы займемся позднее, а сейчас попробуем несколько расширить наши представления о случайной величине 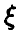 , составленные по выборке.
, составленные по выборке.
Параметры распределений. Точечное оценивание
Пусть в эксперименте  изучается случайная величина
изучается случайная величина 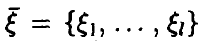 с законом распределения
с законом распределения 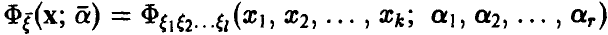 , зависящим от некоторых параметров
, зависящим от некоторых параметров 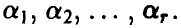
Например, если случайная величина 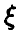 — нормальная, то ее закон распределения зависит от двух параметров —
— нормальная, то ее закон распределения зависит от двух параметров — 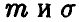 , если
, если 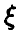 — равномерная на промежутке [а, b], то параметрами закона распределения являются концы а и b, и т. д.
— равномерная на промежутке [а, b], то параметрами закона распределения являются концы а и b, и т. д.
Пусть 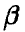 — один из подобных параметров. Попробуем по выборке, полученной в результате эксперимента, высказать некоторое суждение о возможных значениях параметра
— один из подобных параметров. Попробуем по выборке, полученной в результате эксперимента, высказать некоторое суждение о возможных значениях параметра 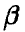 .
.
Для этого сначала следует указать способ вычисления величины 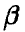 по выборке
по выборке

т. е. функцию b от n векторных переменных такую, что

а потом пояснить, как в соотношении (12) понимать знак приближенного равенства.
Пусть, к примеру, 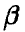 — это математическое ожидание случайной величины
— это математическое ожидание случайной величины 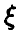 . Тогда, как показано в предыдущем параграфе, в качестве функции b можно взять среднее арифметическое наблюденных значений и при этом понимать равенство в соотношении (12) как «равенство в большинстве случаев», т. е. вероятность больших отличий левой части от правой мала.
. Тогда, как показано в предыдущем параграфе, в качестве функции b можно взять среднее арифметическое наблюденных значений и при этом понимать равенство в соотношении (12) как «равенство в большинстве случаев», т. е. вероятность больших отличий левой части от правой мала.
Формализуя вышеизложенное, скажем, что оценкой неизвестного параметра 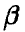 будем называть функцию
будем называть функцию 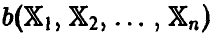 от наблюденных значений такую, что
от наблюденных значений такую, что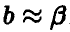 .
.
Ясно, что нас будут интересовать не любые оценки параметра 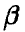 , а только те, которые в некотором смысле на него похожи. Критериев «похожести», т. е. интерпретаций приближенного равенства в соотношении (12), существует много. Мы рассмотрим здесь наиболее употребительные.
, а только те, которые в некотором смысле на него похожи. Критериев «похожести», т. е. интерпретаций приближенного равенства в соотношении (12), существует много. Мы рассмотрим здесь наиболее употребительные.
Оценка 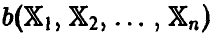 называется состоятельной оценкой неизвестного параметра
называется состоятельной оценкой неизвестного параметра 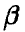 , если вероятность отклонений
, если вероятность отклонений 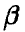 от
от 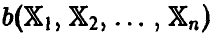 становится малой с ростом n
становится малой с ростом n
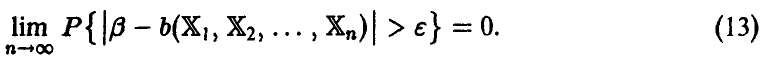
В соответствии с этим определением (как следует из теорем 1 и 2) эмпирические моменты являются состоятельными оценками соответствующих теоретических моментов. Состоятельность — это «похожесть в большинстве случаев».
Оценка 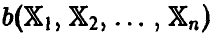 называется несмещенной оценкой параметра
называется несмещенной оценкой параметра 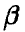 , если
, если

Несмещенность оценки есть ее похожесть на оцениваемый параметр «в среднем», т. е., если мы обладаем несколькими выборками
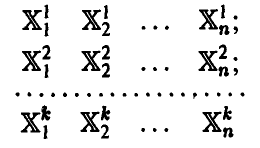
и по каждой из них найдем оценку 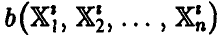 , то эти числа будут одинаково часто как превышать истинное значение оцениваемого параметра
, то эти числа будут одинаково часто как превышать истинное значение оцениваемого параметра 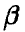 , так и не превосходить его, т. е. отклонение оценки от оцениваемого параметра в случае несмещенности оценки носит несистематический характер.
, так и не превосходить его, т. е. отклонение оценки от оцениваемого параметра в случае несмещенности оценки носит несистематический характер.
Пример:
Эмпирическая оценка математического ожидания является несмещенной оценкой
 Мы хотим доказать, что
Мы хотим доказать, что
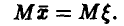
Рассмотрим
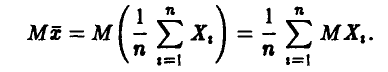
Так как 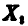 — независимые в совокупности случайные величины, каждая из которых совпадает с
— независимые в совокупности случайные величины, каждая из которых совпадает с 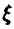 , то
, то 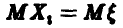 и мы получаем
и мы получаем
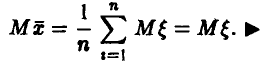
Пример:
Эмпирическая оценка дисперсии
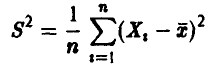
не обладает свойством несмещенности.
 Действительно
Действительно
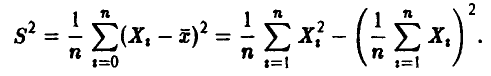
Поэтому
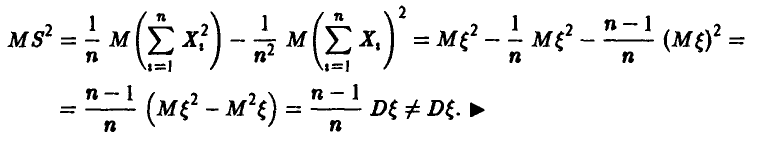
Несмещенную оценку дисперсии можно легко построить. Как показано выше,
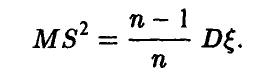
Поэтому
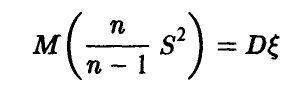
и, следовательно, исправленная величина 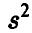 , определяемая соотношением
, определяемая соотношением
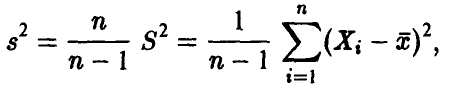
есть несмещенная оценка дисперсии.
С практической точки зрения свойство состоятельности очень важно — его наличие позволяет надеяться, что с увеличением объема выборки точность оценивания будет расти (конечно, только в подавляющем большинстве случаев). Несмещенность же играет менее важную роль. Если оценка является несмещенной, то это свидетельствует об отсутствии систематической ошибки в оценивании неизвестного параметра. Указанное обстоятельство становится важным в случае малых выборок, когда оценки могут быть далеки от оцениваемого параметра и наличие систематической погрешности оценивания только ухудшает точность оценивания. В случае больших выборок смещение оценки (при наличии состоятельности!) на точность оценивания существенного влияния не оказывает.
Важно также понимать, что вышеизложенное имеет смысл только если выполнены условия применимости законов больших чисел, на выводах из которых базируются наши заключения. Важнейшим из подобных условий является существование математического ожидания исследуемой случайной величины 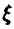 .
.
Рассмотрим некоторые методы нахождения оценок неизвестных параметров распределения, сделав дополнительное предположение, а именно: пусть вид функции распределения случайной величины 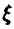 известен
известен
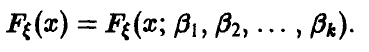
Итак, в результате эксперимента получена выборка объема n. Требуется по выборке найти оценки неизвестных параметров 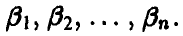
Метод моментов
Идея метода моментов состоит в приравнивании эмпирических моментов, найденных по выборке, соответствующим теоретическим, которые зависят от неизвестных параметров 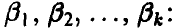
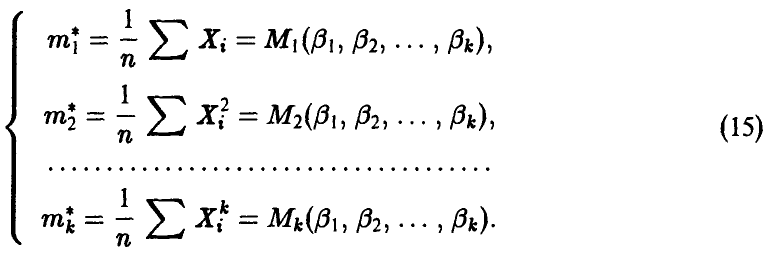
Система (15) позволяет выразить неизвестные параметры 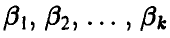 через выборочные значения
через выборочные значения 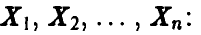
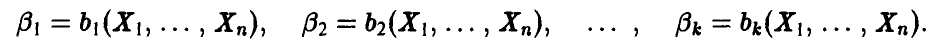
Функции  и считаются оценками параметров
и считаются оценками параметров 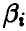 . Близость оценок, найденных по методу моментов, к истинным значениям оцениваемых параметров описывается следующей теоремой.
. Близость оценок, найденных по методу моментов, к истинным значениям оцениваемых параметров описывается следующей теоремой.
Теорема:
Пусть решение системы (15) существует, причем функции
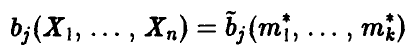
непрерывны в точке 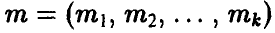 . Тогда оценки, полученные по методу моментов, состоятельны.
. Тогда оценки, полученные по методу моментов, состоятельны.
Оценки, полученные по методу моментов, необязательно являются несмещенными. Однако, если наложить на функции 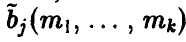 некоторые дополнительные ограничения, то можно получить утверждение, касающееся асимптотической несмещенности оценок, найденных методом моментов
некоторые дополнительные ограничения, то можно получить утверждение, касающееся асимптотической несмещенности оценок, найденных методом моментов
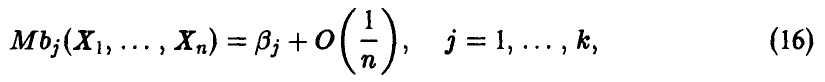
т. е. смещение оценки с ростом объема выборки убывает.
На практике метод моментов приводит к относительно простым вычислениям и, как следует из теоремы, позволяет находить состоятельные оценки параметров. Смещение этих оценок для больших выборок несущественно (16). Кроме того, во всех практически важных случаях это смещение легко устраняется с помощью простых поправок.
Пример:
Известно, что случайная величина 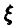 равномерно распределена на отрезке
равномерно распределена на отрезке 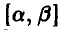 . Получена выборка объема n из распределения случайной величины
. Получена выборка объема n из распределения случайной величины 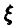 . Оценить величины
. Оценить величины 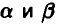
◄ Произведем оценку неизвестных параметров 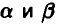 , пользуясь методом моментов. Имеем
, пользуясь методом моментов. Имеем
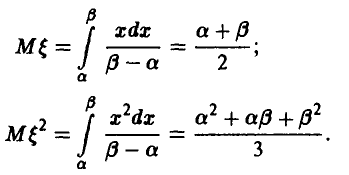
Система (15) в данном случае принимает вид
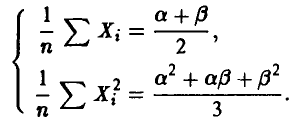
Решая ее относительно 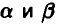 , получаем
, получаем
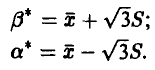
Учитывая, что 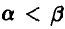 , заключаем, что наша система всегда имеет решение и притом единственное. Полученные оценки состоятельны, однако свойством несмещенности не обладают. ►
, заключаем, что наша система всегда имеет решение и притом единственное. Полученные оценки состоятельны, однако свойством несмещенности не обладают. ►
Пример:
Оценить по выборке параметр 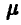 экспоненциально распределенной случайной величины
экспоненциально распределенной случайной величины 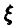 .
.
◄ Функция распределения случайной величины 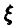 имеет вид
имеет вид
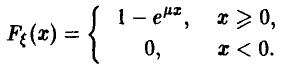
Следовательно,
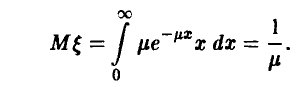
Система (15) сводится к одному уравнению
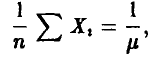
откуда

Полученная оценка состоятельна. Что касается несмещенности, то поскольку 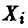 экспоненциально распределены, то
экспоненциально распределены, то 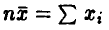 имеет гамма-распределение с плотностью
имеет гамма-распределение с плотностью
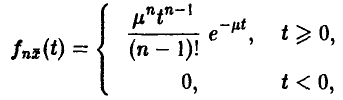
и поэтому
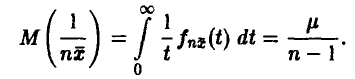
Следовательно, оценка (17) свойством несмещенности не обладает, так как
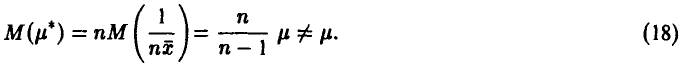
Однако, используя соотношение (18), легко можно получить несмещенную оценку параметра 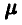
Метод максимального правдоподобия
Пусть 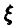 — непрерывная случайная величина с плотностью
— непрерывная случайная величина с плотностью
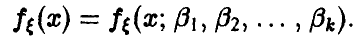
Вид плотности известен, но неизвестны значения параметров 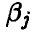
Функцией правдоподобия называется функция
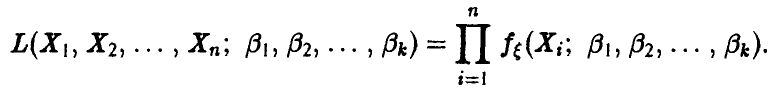
(здесь  — выборка объема n из распределения случайной величины
— выборка объема n из распределения случайной величины 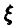 ). Легко видеть, что функции правдоподобия можно придать вероятностный смысл, а именно: рассмотрим случайный вектор
). Легко видеть, что функции правдоподобия можно придать вероятностный смысл, а именно: рассмотрим случайный вектор 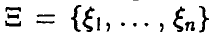 , компоненты которого независимые в совокупности одинаково распределенные случайные величины с законом
, компоненты которого независимые в совокупности одинаково распределенные случайные величины с законом 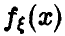 . Тогда элемент вероятности вектора
. Тогда элемент вероятности вектора 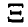 имеет вид
имеет вид
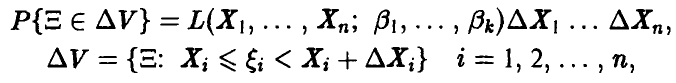
т. е. функция правдоподобия связана с вероятностью получения фиксированной выборки в последовательности экспериментов 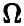 .
.
Основная идея метода правдоподобия состоит в том, что в качестве оценок параметров 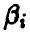 предлагается взять такие значения
предлагается взять такие значения 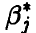 , которые доставляют максимум функции правдоподобия при данной фиксированной выборке, т. е. предлагается считать выборку, полученную в эксперименте, наиболее вероятной. Нахождение оценок параметров
, которые доставляют максимум функции правдоподобия при данной фиксированной выборке, т. е. предлагается считать выборку, полученную в эксперименте, наиболее вероятной. Нахождение оценок параметров 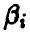 сводится к решению системы k уравнений (k — число неизвестных параметров):
сводится к решению системы k уравнений (k — число неизвестных параметров):
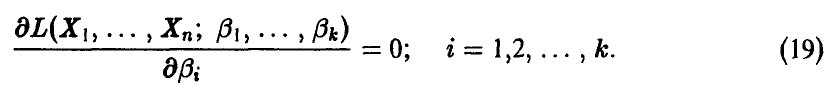
Поскольку функция log L имеет максимум в той же точке, что и функция правдоподобия, то часто систему уравнений правдоподобия (19) записывают в виде
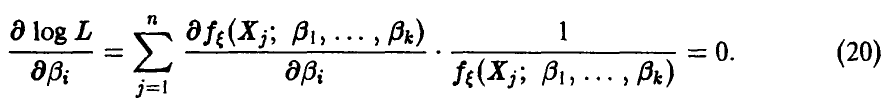
В качестве оценок неизвестных параметров 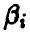 следует брать решения системы (19) или (20), действительно зависящие от выборки и не являющиеся постоянными.
следует брать решения системы (19) или (20), действительно зависящие от выборки и не являющиеся постоянными.
В случае, когда 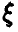 дискретна с рядом распределения
дискретна с рядом распределения 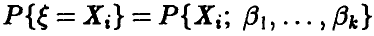
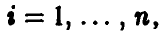 функцией правдоподобия называют функцию
функцией правдоподобия называют функцию
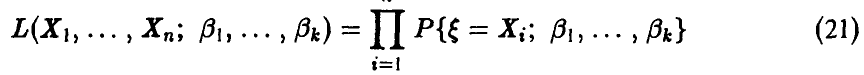
и оценки ищут как решения системы
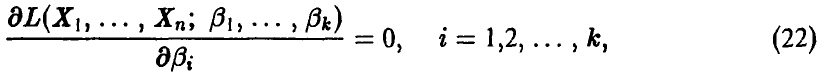
или эквивалентной ей
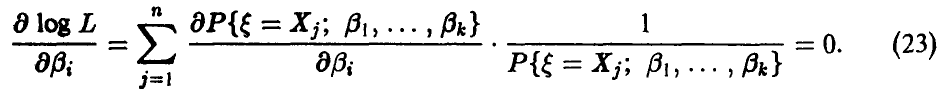
Можно показать, что оценки максимального правдоподобия обладают свойством состоятельности. Следует отметить, что метод максимального правдоподобия приводит к более сложным вычислениям, нежели метод моментов, но теоретически он белее эффективен, так как оценки максимального правдоподобия меньше уклоняются от истинных значений оцениваемых параметров, чем оценки, полученные по методу моментов.
Для наиболее часто встречающихся в приложениях распределений оценки параметров, полученные по методу моментов и по методу максимального правдоподобия, в большинстве случаев совпадают.
Пример:
Отклонение 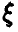 размера детали от номинала является нормально распределенной случайной величиной. Требуется по выборке определить систематическую ошибку и дисперсию отклонения.
размера детали от номинала является нормально распределенной случайной величиной. Требуется по выборке определить систематическую ошибку и дисперсию отклонения.
 По условию
По условию 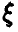 — нормально распределенная случайная величина с математическим ожиданием (систематическая ошибка) и дисперсией, подлежащими оценке по выборке объема
— нормально распределенная случайная величина с математическим ожиданием (систематическая ошибка) и дисперсией, подлежащими оценке по выборке объема 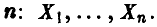 В этом случае
В этом случае
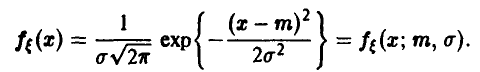
Функция правдоподобия
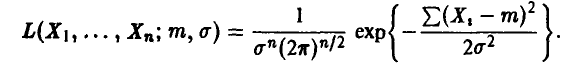
Система (19) имеет вид
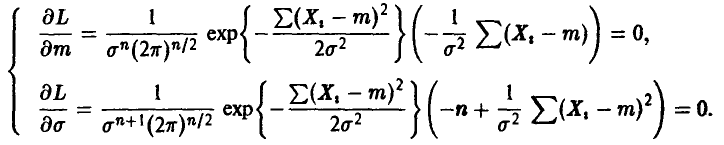
Отсюда, исключая решения, не зависящие от  , получаем
, получаем
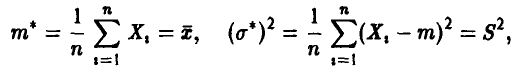
т е. оценки максимального правдоподобия в этом случае совпадают с уже известными нам эмпирическими средним и дисперсией ►
Пример:
Оценить по выборке параметр 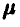 экспоненциально распределенной случайной величины.
экспоненциально распределенной случайной величины.
 Функция правдоподобия имеет вид
Функция правдоподобия имеет вид
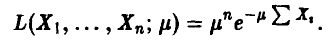
Уравнение правдоподобия
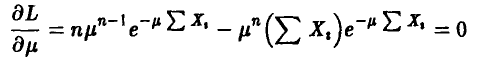
приводит нас к решению
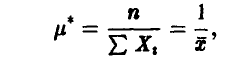
совпадающему с оценкой этого же параметра, полученной по методу моментов, см. (17). ►
Пример:
Пользуясь методом максимального правдоподобия, оценить вероятность появления герба, если при десяти бросаниях монеты герб появился 8 раз.
 Пусть подлежащая оценке вероятность равна р. Рассмотрим случайную величину
Пусть подлежащая оценке вероятность равна р. Рассмотрим случайную величину 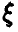 с рядом распределения
с рядом распределения
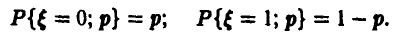
Функция правдоподобия (21) имеет вид
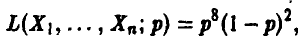
так как
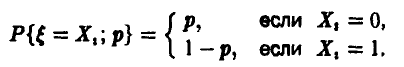
Уравнение правдоподобия
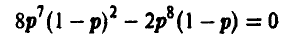
дает в качестве оценки неизвестной вероятности р частоту появления герба в эксперименте
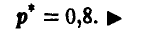
Заканчивая обсуждение методов нахождения оценок, подчеркнем, что, даже имея очень большой объем экспериментальных данных, мы все равно не можем указать точного значения оцениваемого параметра, более того, как уже неоднократно отмечалось, получаемые нами оценки близки к истинным значениям оцениваемых параметров только «в среднем» или «в большинстве случаев». Поэтому важной статистической задачей, которую мы рассмотрим далее, является задача определения точности и Достоверности проводимого нами оценивания.
Интервальное оценивание
Результаты предыдущего параграфа позволяют по выборке определить оценку неизвестного параметра  -распределения
-распределения 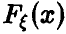 . Эти оценки носят точечный характер — они указывают число, в некотором смысле похожее на оцениваемый параметр, другими словами, они позволяют определить точку
. Эти оценки носят точечный характер — они указывают число, в некотором смысле похожее на оцениваемый параметр, другими словами, они позволяют определить точку 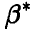 , находящуюся в большей или меньшей близости к истинному значению оцениваемого параметра (рис. 1).
, находящуюся в большей или меньшей близости к истинному значению оцениваемого параметра (рис. 1).
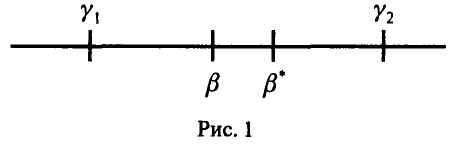
Пусть нам удалось построить две функции 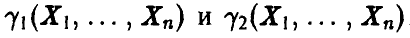 , удовлетворяющие условию
, удовлетворяющие условию
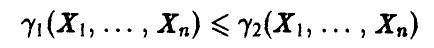
для любых значений 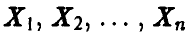 . Рассмотрим на числовой оси промежуток
. Рассмотрим на числовой оси промежуток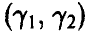 . Его концы
. Его концы 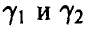 зависят от выборочных значений и, следовательно, являются случайными величинами. Вследствие этого промежуток
зависят от выборочных значений и, следовательно, являются случайными величинами. Вследствие этого промежуток 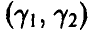 также является случайным в том смысле, что его длина и положение на числовой прямой зависят от выборки
также является случайным в том смысле, что его длина и положение на числовой прямой зависят от выборки 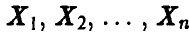 . Истинное значение параметра
. Истинное значение параметра 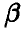 — неслучайное число и его положение на числовой оси фиксировано. Поэтому для некоторых выборок случайный интервал
— неслучайное число и его положение на числовой оси фиксировано. Поэтому для некоторых выборок случайный интервал 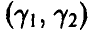 будет накрывать число
будет накрывать число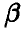 , а для некоторых не будет. Если нам удается подобрать функции
, а для некоторых не будет. Если нам удается подобрать функции 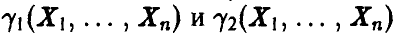 так, что случайный интервал
так, что случайный интервал 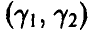 «часто» накрывает истинное значение неизвестного параметра
«часто» накрывает истинное значение неизвестного параметра 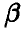 , то мы можем в качестве оценки этого параметра взять любую точку интервала
, то мы можем в качестве оценки этого параметра взять любую точку интервала 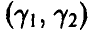 . При этом можно утверждать, что «довольно часто» наша оценка отличается от оцениваемого параметра не более чем на длину интервала
. При этом можно утверждать, что «довольно часто» наша оценка отличается от оцениваемого параметра не более чем на длину интервала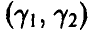 .
.
Введем новое понятие, формализующее выше приведенные рассуждения.
Доверительным интервалом для параметра 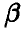 называется случайный интервал
называется случайный интервал 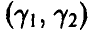 такой, что
такой, что

Число х при этом называется уровнем доверия или доверительной вероятностью.
Выбор числа х — уровня доверия — зависит от того, что мы понимаем под словами «довольно часто», и от того, какой точности в определении параметра /3 мы хотим достичь. Поскольку добиться абсолютной достоверности (чтобы ошибка не превышала длины интервала всегда) мы не можем, то поступимся достоверностью, чтобы получить нетривиальную информацию о точности. Выбирая х очень маленьким, мы, конечно, можем добиться того, чтобы длина интервала 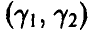 была сколь угодно малой, однако в этом случае (из-за малости х и неравенства (24)) мы крайне редко будем получать доверительный интервал, накрывающий истинное значение параметра
была сколь угодно малой, однако в этом случае (из-за малости х и неравенства (24)) мы крайне редко будем получать доверительный интервал, накрывающий истинное значение параметра 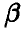 , т. е. найденные нами по конкретным выборкам интервалы будут ненадежны. Выбор же х очень близкого к единице, неоправданно расширяет границы доверительного интервала и тем самым понижает точность определения параметра
, т. е. найденные нами по конкретным выборкам интервалы будут ненадежны. Выбор же х очень близкого к единице, неоправданно расширяет границы доверительного интервала и тем самым понижает точность определения параметра 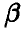 . Поскольку чаще всего нас интересует вопрос, как сильно мы можем ошибиться, заменяя истинное значение параметра
. Поскольку чаще всего нас интересует вопрос, как сильно мы можем ошибиться, заменяя истинное значение параметра 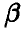 его оценкой
его оценкой 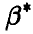 , то обычно доверительную вероятность х выбирают настолько близкой к единице, чтобы с событиями, вероятность которых меньше, чем 1-х, можно было практически не считаться. Соответствующий этой вероятности доверительный интервал дает надежную (с вероятностью х) оценку отличия приближенного значения
, то обычно доверительную вероятность х выбирают настолько близкой к единице, чтобы с событиями, вероятность которых меньше, чем 1-х, можно было практически не считаться. Соответствующий этой вероятности доверительный интервал дает надежную (с вероятностью х) оценку отличия приближенного значения 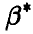 от неизвестного точного
от неизвестного точного 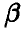 . На практике в качестве х в зависимости от конкретной ситуации выбирают одно из чисел — 0,9; 0,95; 0,99; 0,999.
. На практике в качестве х в зависимости от конкретной ситуации выбирают одно из чисел — 0,9; 0,95; 0,99; 0,999.
Возвращаясь к задаче определения точности и достоверности оценки 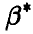 неизвестного параметра
неизвестного параметра 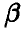 , отметим, что определить точность оценки — значит указать, как велика может быть разница
, отметим, что определить точность оценки — значит указать, как велика может быть разница

Но в силу того, что 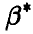 — случайная величина, разность (25) — также случайная величина и может принимать любые значения, причем одни чаще, другие реже. Поэтому тесно связанной с определением точности является задача определения достоверности оценки, т. е. указания той доли случаев, когда величина
— случайная величина, разность (25) — также случайная величина и может принимать любые значения, причем одни чаще, другие реже. Поэтому тесно связанной с определением точности является задача определения достоверности оценки, т. е. указания той доли случаев, когда величина 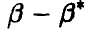 не превосходит некоторой величины
не превосходит некоторой величины 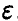 . Суммируя, получаем, что определить точность и достоверность оценки
. Суммируя, получаем, что определить точность и достоверность оценки 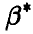 — значит указать числа
— значит указать числа 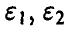 и х такие, что
и х такие, что

т. е. задача определения точности и достоверности оценки 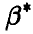 — это задача построения доверительного интервала для параметра
— это задача построения доверительного интервала для параметра 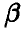 .
.
Заметим, что при 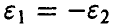 доверительный интервал оказывается симметричным относительно точечной оценки
доверительный интервал оказывается симметричным относительно точечной оценки 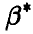 .
.
Точность и надежность оценивания математического ожидания нормальной случайной величины
Пусть 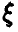 — нормальная случайная величина с параметрами
— нормальная случайная величина с параметрами 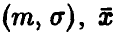 — эмпирическая оценка параметра
— эмпирическая оценка параметра 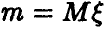 . Существенным для дальнейшего является вопрос о том, известна или нет дисперсия.
. Существенным для дальнейшего является вопрос о том, известна или нет дисперсия.
1. Пусть 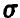 а известна.
а известна.
В силу нормальности 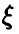 отклонение оценки
отклонение оценки 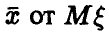 также является нормальной случайной величиной с параметрами
также является нормальной случайной величиной с параметрами
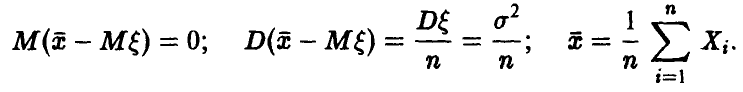
При 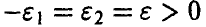 соотношение (26) примет вид
соотношение (26) примет вид
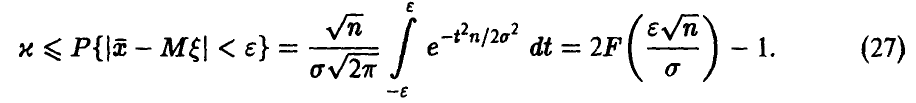
Здесь 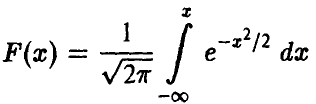 — функция Лапласа. Таким образом, задача свелась к решению уравнения
— функция Лапласа. Таким образом, задача свелась к решению уравнения

относительно 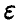 при заданном уровне доверия x. Обозначим решение уравнения
при заданном уровне доверия x. Обозначим решение уравнения
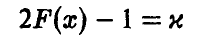
через 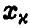 . Тогда
. Тогда

— решение уравнения (28). Искомый доверительный интервал —
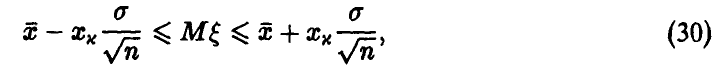
так что в х•100 % случаев неизвестное значение 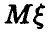 накрывается интервалом (30), т. е. точность в определении
накрывается интервалом (30), т. е. точность в определении 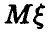 не превышает по модулю величины
не превышает по модулю величины 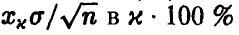 случаев. Правда, в (1 — х) • 100 % случаев найденное нами среднее арифметическое
случаев. Правда, в (1 — х) • 100 % случаев найденное нами среднее арифметическое 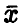
может отличаться от 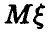 на сколь угодно большую величину, однако за счет того, что события с вероятностью 1 — х практически невозможны, этим можно пренебречь.
на сколь угодно большую величину, однако за счет того, что события с вероятностью 1 — х практически невозможны, этим можно пренебречь.
Отметим, что соотношение (30) — точное, т. е. справедливо для любых объемов экспериментальных данных, в том числе и для малых выборок.
2. Пусть теперь 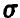 неизвестна.
неизвестна.
В этом случае рассуждения предыдущего пункта мы применить не можем, так как в соотношении (27) значение параметра а нам неизвестно, и мы получим одно уравнение с двумя неизвестными 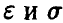 .
.
Рассмотрим величину

Здесь s — исправленная оценка среднеквадратичного отклонения
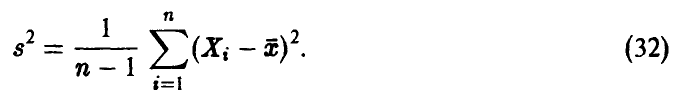
Отметим следующее, важное для дальнейшего, обстоятельство: случайные величины 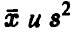 — статистически независимы.
— статистически независимы.
◄ Действительно, случайный вектор
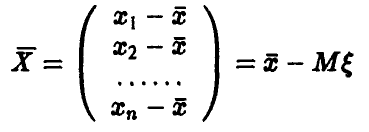
имеет нррмальное распределение, при этом
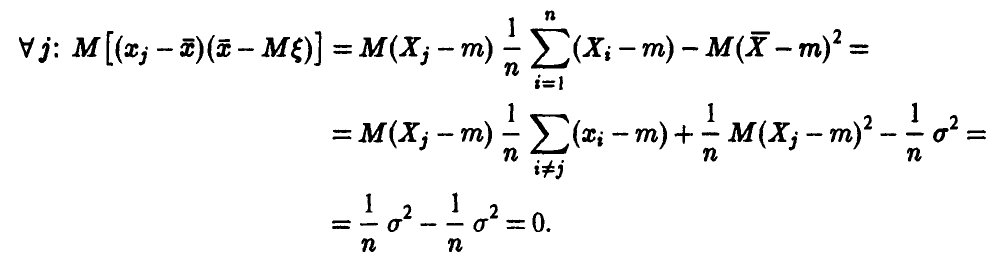
Откуда и следует искомое, так как независимость случайного вектора 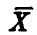 и разности
и разности  влечет независимость случайных величин, являющихся их непрерывными функциями. ►
влечет независимость случайных величин, являющихся их непрерывными функциями. ►
Для величины t, задаваемой соотношением (31), докажем теперь следующую теорему.
Теорема:
Случайная величина
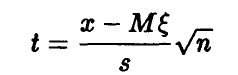
подчиняется распределению Стьюдента с n- 1 степенью свободы.
◄ Заметим, что
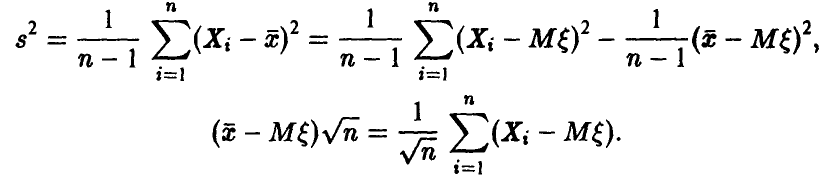
Поэтому
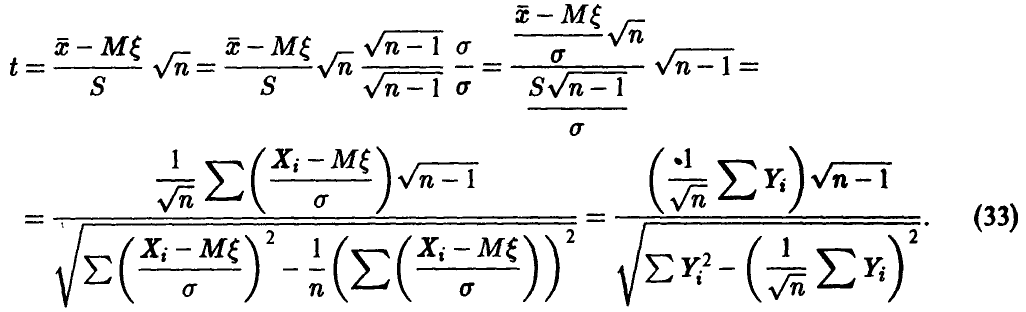
В соотношении (33) через 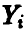 обозначены независимые нормально распределенные случайные величины с параметрами
обозначены независимые нормально распределенные случайные величины с параметрами 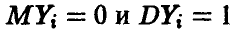
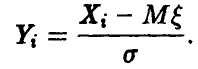
Рассмотрим в n-мерном координатном пространстве 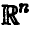 гиперплоскость
гиперплоскость  , задаваемую уравнением
, задаваемую уравнением

Сделаем поворот осей в 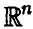 таким образом, чтобы одна из новых координатных осей (для определенности последняя) была бы ортогональна плоскости
таким образом, чтобы одна из новых координатных осей (для определенности последняя) была бы ортогональна плоскости  . При этом Координаты
. При этом Координаты 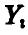 , перейдут в
, перейдут в 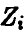 и
и

Поскольку 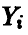 — независимые нормально распределенные случайные величины с параметрами 0 и 1, то и
— независимые нормально распределенные случайные величины с параметрами 0 и 1, то и 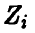 также будут независимыми нормально распределенными случайными величинами с параметрами 0 и 1. Из условия ортогональности одной из новых осей плоскости
также будут независимыми нормально распределенными случайными величинами с параметрами 0 и 1. Из условия ортогональности одной из новых осей плоскости  вытекает, что соответствующая ей новая координата
вытекает, что соответствующая ей новая координата 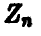 будет иметь вид
будет иметь вид

и
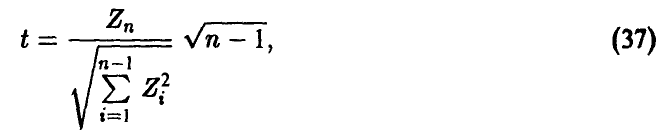
так как
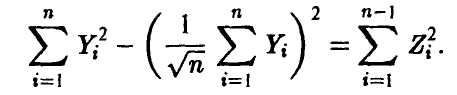
Учитывая независимость 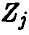 , заключаем, что t имеет распределение Стьюдента с n — 1 степенью свободы. ►
, заключаем, что t имеет распределение Стьюдента с n — 1 степенью свободы. ►
Возвратимся к определению доверительного интервала для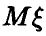 ,
,
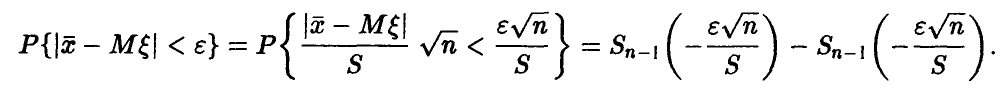
Здесь 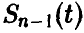 — функция распределения Стьюдента. Последнее уравнение, используя свойство функции
— функция распределения Стьюдента. Последнее уравнение, используя свойство функции 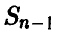
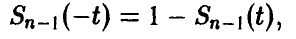
перепишем в виде
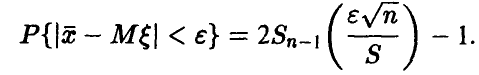
Задавая уровень доверия х и обозначая решение уравнения
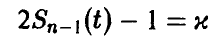
через 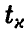 , получаем доверительные границы
, получаем доверительные границы
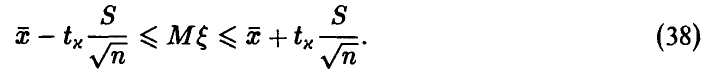
Заметим, что доверительные границы для математического ожидания в случае известной дисперсии 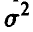 имеют такой же вид. В соотношении (38) вместо среднеквадратического отклонения
имеют такой же вид. В соотношении (38) вместо среднеквадратического отклонения 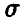 стоит оценка (32) среднеквадратического отклонения s, вместо
стоит оценка (32) среднеквадратического отклонения s, вместо 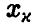 — решения уравнения
— решения уравнения 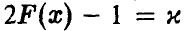 — стоит
— стоит 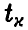 — решение уравнения
— решение уравнения 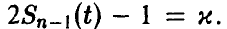 Доверительные границы (38), вообще говоря, шире доверительных границ (30), что объясняется большей долей неопределенности при нахождении
Доверительные границы (38), вообще говоря, шире доверительных границ (30), что объясняется большей долей неопределенности при нахождении 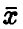 по выборке в случае, когда дисперсия неизвестна, по сравнению со случаем, когда дисперсия известна.
по выборке в случае, когда дисперсия неизвестна, по сравнению со случаем, когда дисперсия известна.
Как и в случае известной 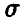 , интервал (38) — точный и может быть использован для оценивания математического ожидания по выборкам любого объема, в том числе и по малым выборкам.
, интервал (38) — точный и может быть использован для оценивания математического ожидания по выборкам любого объема, в том числе и по малым выборкам.
Точность и надежность оценивания дисперсии
нормальной случайной величины
Пусть 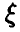 — нормальная случайная величина с параметрами
— нормальная случайная величина с параметрами 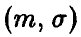 , которые оцениваются по выборке объема n
, которые оцениваются по выборке объема n
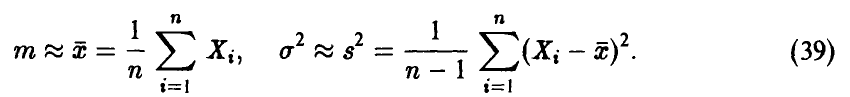
Величина 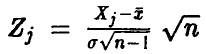 нормальна с параметрами (0,1). Действительно,
нормальна с параметрами (0,1). Действительно, 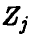 является линейной комбинацией нормальных величин
является линейной комбинацией нормальных величин 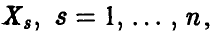
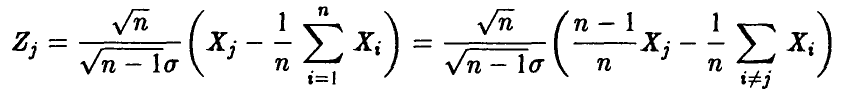
с параметрами 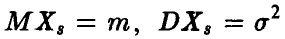 , а потому
, а потому 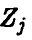 — нормальна. Далее, очевидно,
— нормальна. Далее, очевидно,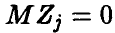 и
и
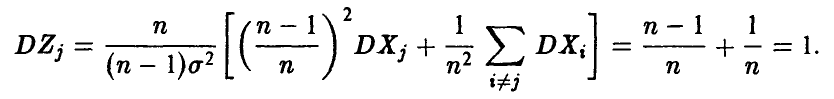
Исправленная оценка дисперсии 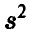 представляется в виде
представляется в виде
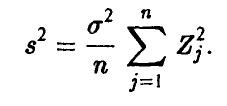
Можно установить, что величина 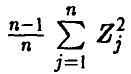 имеет распределение
имеет распределение 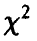 с n — 1 степенью свободы, т. е. распределена как сумма квадратов n — 1 независимых нормальных (0,1) случайных величин, что дает возможность вычислять вероятности
с n — 1 степенью свободы, т. е. распределена как сумма квадратов n — 1 независимых нормальных (0,1) случайных величин, что дает возможность вычислять вероятности
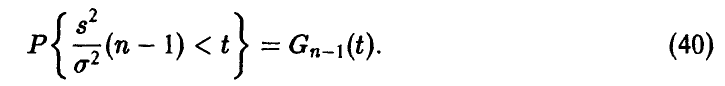
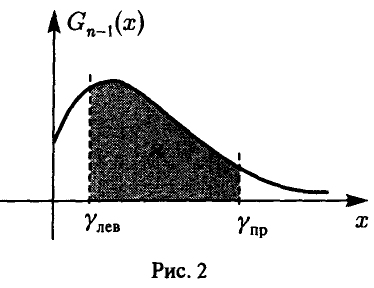
Зададим некоторую вероятность 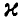 , близкую к единице, и найдем числа
, близкую к единице, и найдем числа 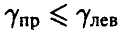 такие, что
такие, что
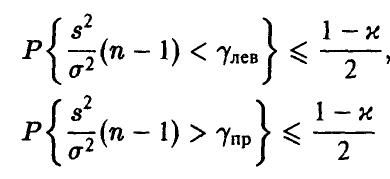
(рис. 2). При этом для неизвестной дисперсии 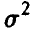 получим
получим
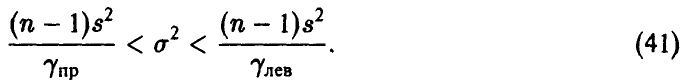
Числа 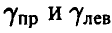 легко определяются как решения уравнений
легко определяются как решения уравнений
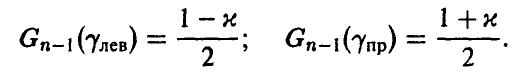
Теперь в качестве точечной оценки неизвестной дисперсии можно взять любое число 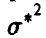 из промежутка (41) и с надежностью х точность такого оценивания будет не хуже, чем
из промежутка (41) и с надежностью х точность такого оценивания будет не хуже, чем
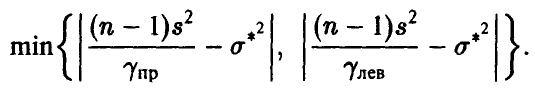
Для симметричной оценки,
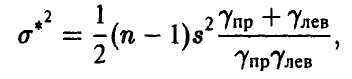
точность 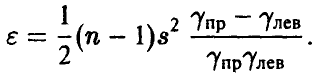
Отметим, что если в качестве точечной оценки взять исправленную оценку дисперсии 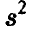 , то интервал (41) относительно этой оценки симметричным не будет.
, то интервал (41) относительно этой оценки симметричным не будет.
Точность и надежность оценивания для негауссовских распределений
Результаты предыдущего параграфа позволяют найти точные доверительные интервалы для математического ожидания и дисперсии нормальной случайной величины, при условии ее нормальности. Если же случайная величина 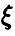 имеет произвольную функцию распределения, то это удается уже не всегда. Однако, если объем выборки достаточно велик, то можно указать приближенные доверительные интервалы границы для моментов случайной величины
имеет произвольную функцию распределения, то это удается уже не всегда. Однако, если объем выборки достаточно велик, то можно указать приближенные доверительные интервалы границы для моментов случайной величины 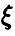 , используя следующее утверждение.
, используя следующее утверждение.
Теорема:
Пусть
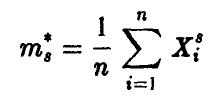
— эмпирическая оценка момента 8-го порядка случайной величины существование которого предполагается. Тогда случайная величина

распределена асимптотически нормально с параметрами 0 и 1,

Отсюда следует, что
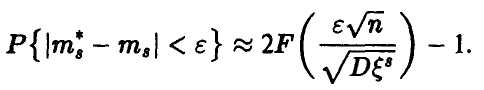
Задавая уровень доверия и и решая уравнение
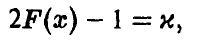
получаем значение 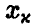 такое, что
такое, что
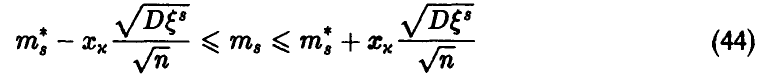
с вероятностью 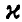 . И, если известна
. И, если известна 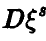 , то соотношение (44) дает искомый доверительный интервал.
, то соотношение (44) дает искомый доверительный интервал.
Замечание:
Нормальное распределение дает плохое приближение к истинному распределению суммы 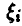 в области вероятностей очень малых или очень близких к единице. Поэтому доверительные интервалы (44) очень грубы уже при р > 0,999. В некоторых случаях удается оценить относительную ошибку, которая получается при замене истинного распределения суммы большого числа случайных величин нормальным распределением, и построить более точные интервалы.
в области вероятностей очень малых или очень близких к единице. Поэтому доверительные интервалы (44) очень грубы уже при р > 0,999. В некоторых случаях удается оценить относительную ошибку, которая получается при замене истинного распределения суммы большого числа случайных величин нормальным распределением, и построить более точные интервалы.
Если же 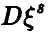 неизвестна, то обычно ее заменяют оценкой
неизвестна, то обычно ее заменяют оценкой
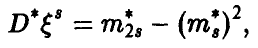
еще более снижая точность доверительного интервала (44).
Пример:
Построить доверительный интервал для математического ожидания нормальной случайной величины, если по выборке объема n = 21 построены оценки 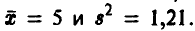 Уровень доверия х = 0,999.
Уровень доверия х = 0,999.
 Точный доверительный интервал имеет вид
Точный доверительный интервал имеет вид
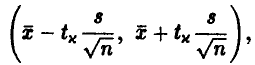
где 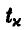 — решение уравнения
— решение уравнения
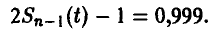
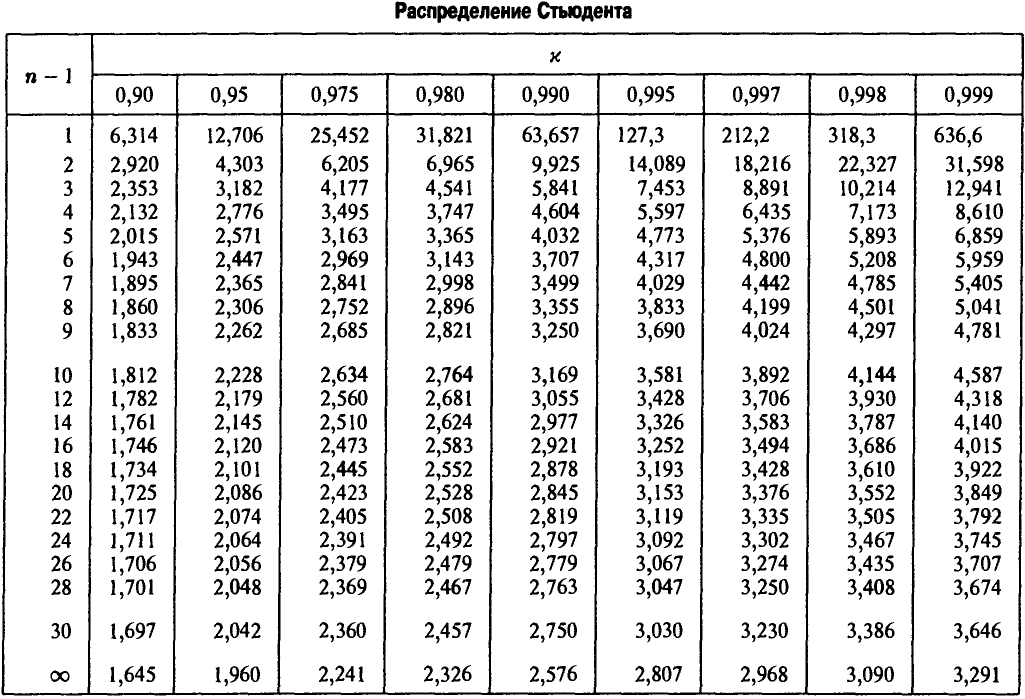
В нашем случае n — 1 = 20, x = 0,999. По таблице распределения Стьюдента (см. ниже) определяем 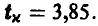 Искомый доверительный интервал имеет границы
Искомый доверительный интервал имеет границы
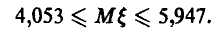
Приближенный доверительный интервал с тем же уровнем доверия выглядит так:
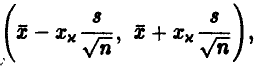
где 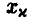 — решение уравнения
— решение уравнения
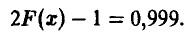
По таблице нормального распределения (см. с. 69) определяем 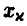 = 3,3 и искомый доверительный интервал
= 3,3 и искомый доверительный интервал
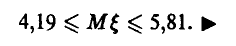
► Заметим, что точный доверительный интервал оказался более осторожным, чем приближенный. Этого и следовало ожидать.
С увеличением же объема выборки приближенный доверительный интервал становится более близок к точному. Действительно, пусть данные нашей задачи получены по выборке объема n = 50. Тогда 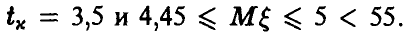 В то же время,
В то же время, 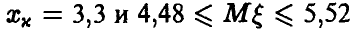 и разница между точным и приближенным доверительными интервалами уменьшилась.
и разница между точным и приближенным доверительными интервалами уменьшилась.
Эффективность оценивания. Неравенство Рао—Крамера
При оценивании естественно считать дисперсию оценок мерилом того, насколько хороша или плоха принятая процедура. Если 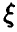 — случайная величина с законом распределения
— случайная величина с законом распределения 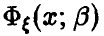 и для оценивания параметра
и для оценивания параметра 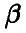 мы имеем две различные процедуры
мы имеем две различные процедуры 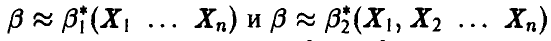 с дисперсиями
с дисперсиями 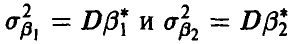 соответственно, то при
соответственно, то при 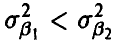 оценка
оценка 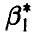 считается лучше оценки
считается лучше оценки 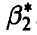 . Для больших выборок этот показатель не очень существен, ибо, как следует из полученных выше соотношений (30), (38) и (44), при
. Для больших выборок этот показатель не очень существен, ибо, как следует из полученных выше соотношений (30), (38) и (44), при  точность оценивания убывает как
точность оценивания убывает как 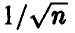 и стремится к нулю независимо от
и стремится к нулю независимо от 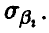
Однако для малых выборок вопрос о выборе наилучшей в указанном смысле оценки приобретает важное значение. Мы получим ответ на него при дополнительном предположении о несмещенности рассматриваемых оценок.
Пусть 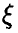 — случайная величина, плотность распределения которой
— случайная величина, плотность распределения которой 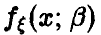 зависит от одного параметра
зависит от одного параметра 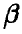 . Пусть, далее,
. Пусть, далее, 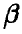 оценивается по выборке объема n несмещенным образом
оценивается по выборке объема n несмещенным образом
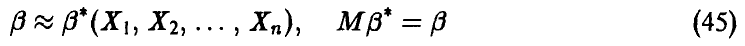
И (см. п. 1.2.2.) функция правдоподобия выборки 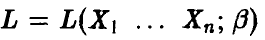 определяется соотношением
определяется соотношением
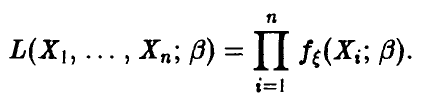
Тогда имеет место утверждение
Теорема Неравенство Рао—Крамера:
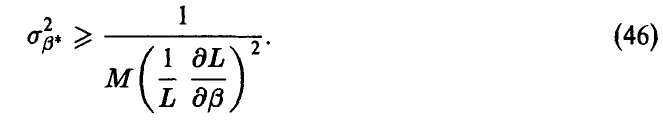
◄ Для сокращения записи положим
И с учетом этих обозначений получим
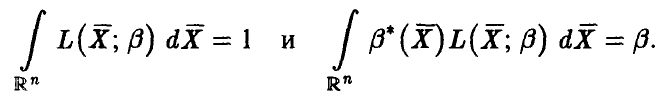
Первое из соотношений следует из того, что функция правдоподобия есть плотность распределения вектора 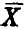 выборочных значений
выборочных значений  , второе — из несмещенности оценки
, второе — из несмещенности оценки 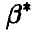 . Дифференцируя эти соотношения по
. Дифференцируя эти соотношения по 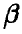 и вычитая результаты дифференцирования, получаем
и вычитая результаты дифференцирования, получаем
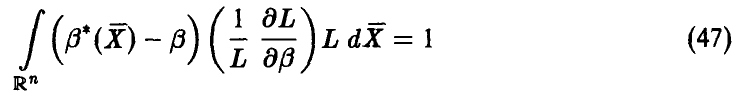
или
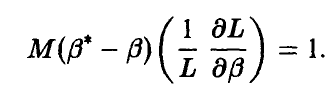
Из неравенства Коши—Буняковского для математических ожиданий заключаем, что
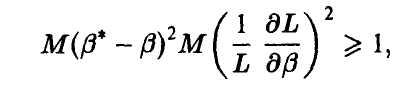
чем доказательство и завершается. ►
Неравенство (46) при помощи несложных выкладок может быть переписано в несколько более удобном для практического использования виде. А именно, поскольку
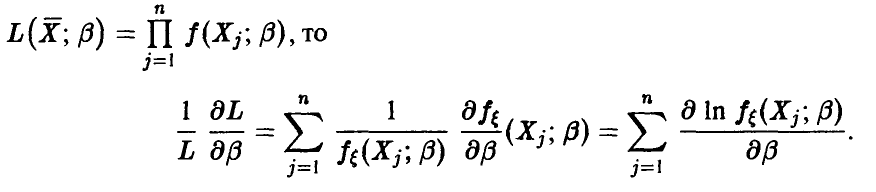
Функции 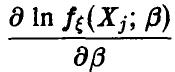 независимы в силу независимости выборочных значений
независимы в силу независимости выборочных значений 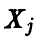
Поєтому 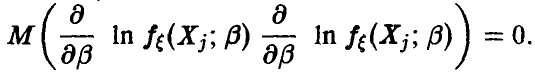 С учетом этого замечания
С учетом этого замечания
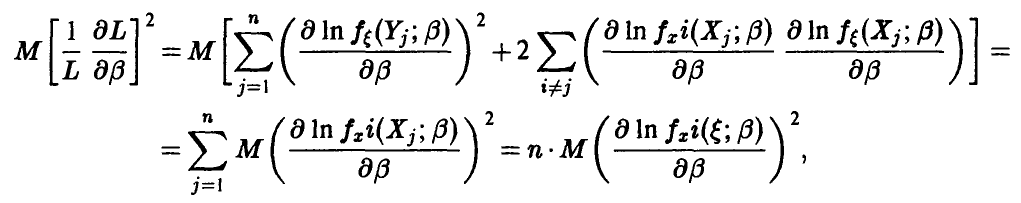
и неравенство (46) принимает вид
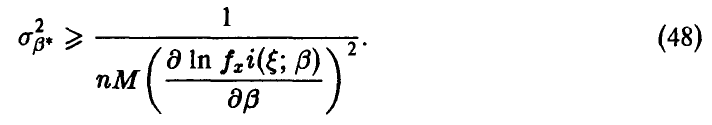
Пример:
В важном для приложений случае оценивания математического ожидания нормальной случайной величины 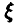 получаем
получаем
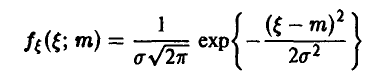
и (48) записывается в виде
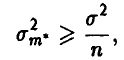
где 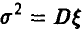 . Заметим, что для эмпирической оценки математического ожидания
. Заметим, что для эмпирической оценки математического ожидания 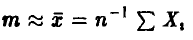 выполняется
выполняется
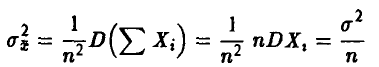
и, следовательно, с рассматриваемой точки зрения эта оценка наилучшая.
Такие оценки в статистике называются эффективными.
Аналогичная теорема может быть доказана и для случая совместного оценивания нескольких неизвестных параметров распределения. Здесь мы ограничимся только формулировкой указанной теоремы.
Пусть, как и выше, 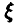 — непрерывная случайная величина с плотностью
— непрерывная случайная величина с плотностью 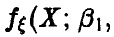
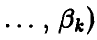 , зависящей от вектора параметров
, зависящей от вектора параметров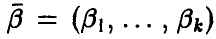 , несмещенная оценка которого дается соотношениями
, несмещенная оценка которого дается соотношениями
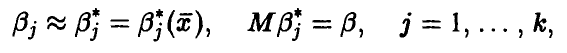
и 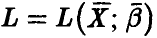 — функция правдоподобия выборки
— функция правдоподобия выборки 
Пусть далее
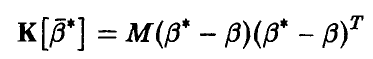
и
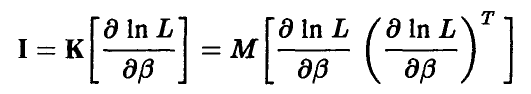
— корреляционные матрицы вектора оценок  и градиента логарифма функции правдоподобия, соответственно:
и градиента логарифма функции правдоподобия, соответственно:
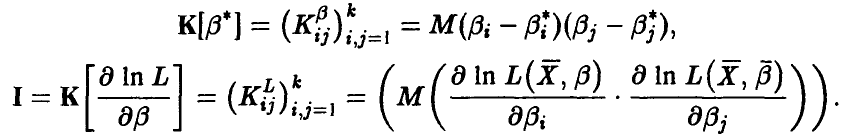
Тогда, в предположении, что матрица I обратима, имеет место неравенство

которое следует понимать как неотрицательную определенность матрицы 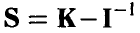 , т. е.
, т. е. 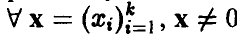 , выполняется неравенство
, выполняется неравенство

Решение заданий и задач по предметам:
Дополнительные лекции по теории вероятностей:
- Случайные события и их вероятности
- Случайные величины
- Функции случайных величин
- Числовые характеристики случайных величин
- Законы больших чисел
- Статистическая проверка гипотез
- Статистическое исследование зависимостей
- Теории игр
- Вероятность события
- Теорема умножения вероятностей
- Формула полной вероятности
- Теорема о повторении опытов
- Нормальный закон распределения
- Определение законов распределения случайных величин на основе опытных данных
- Системы случайных величин
- Нормальный закон распределения для системы случайных величин
- Вероятностное пространство
- Классическое определение вероятности
- Геометрическая вероятность
- Условная вероятность
- Схема Бернулли
- Многомерные случайные величины
- Предельные теоремы теории вероятностей
- Оценки неизвестных параметров
- Генеральная совокупность

