Оглавление:








Статически неопределимые системы
- Статически неопределенная система. Возможность рассчитать деформацию стержня при растяжении и сжатии дает возможность установить, как будут изменяться форма и размеры частей конструкции под действием внешних сил. Однако существует целый класс конструкций, для которых испытание на прочность и определение сечений отдельных элементов невозможно без возможности определения деформации. Во всех рассмотренных примерах сила растяжения или сжатия стержня определялась из условий статики твердого тела. Поэтому, если подвешивание груза Q на двух стержнях(рис. 38) получаем силу N t и TV2 для
вытягивания стержня EGI из равновесного состояния Точки AB и AC A. Таким образом, число неизвестных (два) равно числу уравнений (два), и мы можем найти силы этих уравнений L/1 и L\2. Эта задача может быть определена статически. Это будет иметь место, если груз Q подвешен на трех стержнях (рис. 39). В этом случае точка А находится в столь же статически неопределенной системе. Состав вытеснения Структура не деформируется, происходит отделение этих разрывов друг от друга § 19] Е С и И под действием четырех сил: Q, A / 3, причем последние три неизвестны.
Уравнения равновесия все еще могут писать только два. Следовательно, число неизвестных ньютон Людмила Фирмаль
Единица больше числа уравнений-структура некогда статически неопределима, и задача не может быть решена только с помощью статических уравнений. Дополнительные уравнения, необходимые для решения задачи, можно перенести из теоретической механики на сопротивление материала, используя полученные нами представления о свойствах материала. Речь идет об учете деформируемости материала. Изучая деформацию, которую испытывает структура, можно найти дополнительные уравнения. Оказывается, всегда можно найти необходимое число
дополнительных уравнений, так что общее число уравнений вместе со статистическими условиями равно числу неизвестных. Эти дополнительные уравнения составляются на основе одного общего принципа, штамп должен выражать условия совместимости варианта системы. Чтобы ни один из стержней не был предоставлен одной схемой конструкции другим или другим. Это совместимость вариантов элементов системы. Общий способ вычисления статически неопределенной системы заключается в следующем: После этого создайте дополнительное уравнение такого числа, чтобы можно было найти все неизвестные силы. Прохождение раствора будет найдено
- в специальном примере, взятом(рис. 39). Пусть крайние стержни с одинаковой площадью поперечного сечения-стальные, промежуточные стержни-медные. Средняя длина штанги Z3, крайняя Zt; допустимое-допустимое давление для стали[OS] и меди[am]для соответствующей. Необходимо установить прочные размеры поперечных сечений этих стержней под действием нагрузки q, которая на них подвешена. Сначала установите силу, действующую на каждую из трех палочек. Поскольку точки A, B, C и D имеют шарниры, все компоненты стержня могут подвергаться только осевому усилию. Для их определения необходимо учитывать равновесие в точке А, где применяются только расчеты статически неопределенных систем. IV Известна сила Q. На схеме координатных осей было дано действие сил на точки и места на рисунке. Сумма
проекций на оси силы, действующей на 40 очков уменьшается до нуля: Н * грех-грех 7Vt=0, м-Н3-потому что-/V2cos а=0. Из первого уравнения мы получаем Ni=L / 2; вместо того, чтобы подставлять значение A/t в уравнение TV2, мы получаем: W3+27Vt cos a=Q. (4.1) теперь у нас есть два неизвестных Чтобы получить дополнительное уравнение, нужно обратиться к исследованию деформации конструкции. Под действием силы Q все три стержня удлиняются и точка A падает. Так как силы и 2V2 равны друг другу, а стержни 7 и 2 из одного и того же материала являются стержнями одинаковой длины, то их удлинения D/i и D/2 одинаковы, и точка A падает вертикально. Называется ли третье удлинение стержня D7?. Чтобы найти новое расположение этой точки, мы вырезаем и рисуем
на ней стержень(см. рис. 41) новую длину крайних стержней SS2 и BB2, увеличив их старую длину на значения D= = AB2 и D72=AS2. Чтобы Людмила Фирмаль
найти новое положение точки A, необходимо вращать удлиненные стержни SS3 и BB вокруг точек B и C. точки B2 и C2 совпадают с точками AI, движущимися по дуге C2At и 2A2, которые могут принимать малость деформации за счет прямых линий, перпендикулярных точкам C2 и BB2. Новые положения крайних стержней VAG и SAG обозначены пунктирной линией. Так как конец среднего стержня также прикреплен к шарниру, то переходим к точке AI, а удлинение D73 равно отрезку AAR всех трех D/R-D/2 и d73§ 191 статически неопределимых систем, соответствующих закону Гука. Из соотношения между этими удлинениями мы получаем дополнительное уравнение, связывающее неизвестную силу в стержне. Из треугольника A^ABмы имеем: AB3-AAI cos OS или
Az3cos a. (4.2) AZT и AZ3 представлены n и N3. Для этого нужно знать площадь этих стержней. Здесь будет важной особенностью статически неопределенной системы: чтобы найти силы в стержнях, необходимо предварительно определить размер их поперечного сечения или их соотношение. Пусть площадь поперечного сечения стержня равна Fx и F3;модуль упругости стали отображает EC и модуль упругости CU E. Затем Д / 1 Ма (4.3 )) Подставляя эти значения для AZt и AZ3 в выражение (4.2; м l_ml EcFt-E MFZ Кос а Итак, Абд из треугольника (рис. 41) следует Зет Три. =ЗТ потому что, Это М=^3^П О с»». (4.4) поэтому, рассматривая совместимость деформации системы, получается дополнительная формула, соединяющая M и L / 3. Для такой конструкции возможна только система усилий, удовлетворяющая условиям равновесия; существует равный ряд
уравнений статики в виде неизвестных, например, соответствие деформаций на конструкции, показанной на рисунке. 38-это небольшая деформация из равновесного состояния Точки а, сила стержня полностью определяется; оба стержня, не нарушая связи друг с другом, могут подвергаться удлинению, вызванному этими силами-требования совместимости деформации удовлетворяются автоматически. И наоборот, в статически неопределенных структурах неизвестное число больше, чем число этих уравнений, поэтому возможно, что существует система любого числа сил, которой
уравнение равновесия удовлетворяет вычислениям статически неопределенных систем[CHAP. IV В статически неопределенных системах (рис. 39) положение точки А после деформации соединяет воедино удлинение всех трех стержней; для того чтобы проследить совместимость деформации, необходимо, чтобы эти удлинения находились в определенном соотношении. Продолжая решать нашу задачу, подставим значение Ni из (4.4) В выражение (4.1), чтобы получить его: +2W3fa АР s’а = с мг3 И так оно и есть. Н3= (4-5) С (4.4) Q 1Ф-2COS3a EUFS (4.6) Из полученной формулы видно, что величина силы N зависит не от абсолютного значения области F и модуля E,
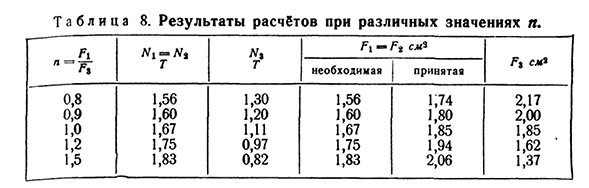
а от их соотношения. Учитывая другое соотношение n=^ -, мы * 8 Это будет Н lt7V3 получает различные комбинации сил. Значения этих сил и допустимое напряжение позволяют найти значения Ft и F3 из следующих условий М Ф (4.7) Найти^3=-путем определения из первого условия Ft и зная значение, выбранное n=Q—. Затем проверьте, соответствует ли G3 Соответствует ли оно второму условию (4.7); в противном случае находим F3 из этого условия, Fx определяется по формуле Fv=nFz. (4.8) поэтому в статически неопределенной системе при заданной нагрузке может быть реализовано множество вариантов распределения сил между стержнями., Давайте рассмотрим численный пример, чтобы
дополнительно проиллюстрировать отношение площади поперечного сечения стержней. Пусть Q4t; а=30°;[ас]=1000 кг[см\£с=2 ′ 106кг] см;(а j=600 кг[см\£»=! 106 кг] см.19] статически неопределимой системы 77 О предварительном подсчете、 Затем 2•10\’\’ 4™coss2 30° М=В8= ——4 ^ 5 ———— = 1,67 г, 1+2GPO » cos ’ 30° Четыре. Л^з о jae1>11г я+2ч я cos3 30° От требований к прочности мы получаем: R_M_1670 Г1-[АУ]-1000=1. 67cm2. Так как мы предполагаем / 71= / 73, F3=1. 67 см2. При таких условиях проверим, удовлетворяет ли условие прочности промежуточного стержня:^ — =^|^=667кг! См, см, 600 кг[см\ \ принятая площадь F3 мала; нужно взять 11ю-1§ 5 и М * 600-см • Чтобы выполнить условие Z71=F3, которое лежит в основе наших расчетов, мы должны принять требуемое значение 1,67 СМ1 из первого условия, а не Z71=Z73=1,85 см2. Поэтому в крайнем стержне есть дополнительный запас прочности.
Смотрите также:

