Пример задачи 8.4
Стальная полоса прямоугольного поперечного сечения, имеющая выточки (рис. 8.11, а)у нагружена растягивающими силами F = 20 кН по продольной оси Z.
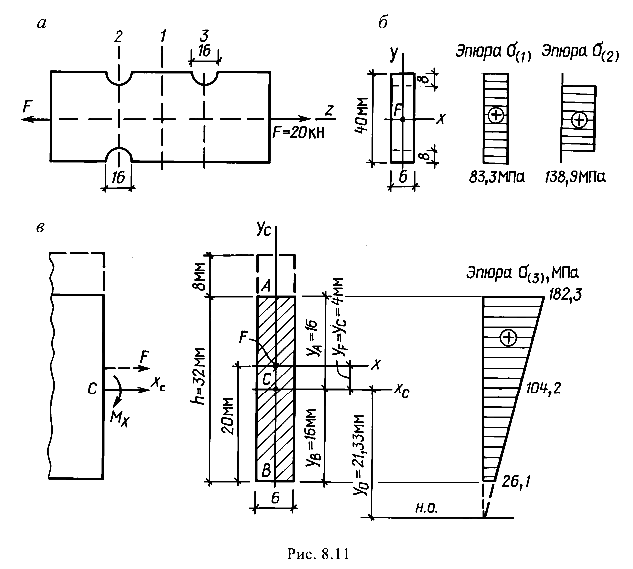
Проверить прочность полосы, если R = 210 МПа. Построить эпюры напряжений в характерных сечениях полосы. Концентрацией напряжений у выточек пренебречь.
Решение
На полосе выделяются три характерных сечения. Внешние силы F, действующие по продольной оси полосы, в сечениях, где нет выточки (1) и где они симметричны (2), создают деформацию центрального растяжения, так как линия действия силы F совпадает с центром тяжести этих сечений (рис. 8.11, б), а в сечении с асимметричной выточкой (3) — внецентренное растяжение, так как линия действия силы смещена относительно центра тяжести этого сечения (рис. 8.11, в).
Определим нормальные напряжения в названных сечениях:
сечение 1:
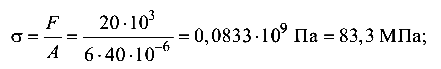
сечение 2:
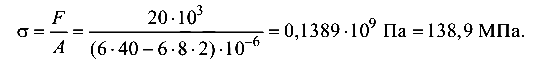
Для сечения 3 воспользуемся формулой (8.4)
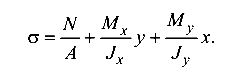
Определим необходимые геометрические характеристики рас сматриваемого сечения. Высота сечения
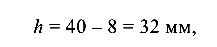
ширина b = 6 мм, площадь
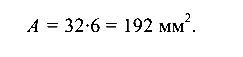
Положение центра тяжести сечения (т. С) и положение главных центральных осей (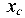
,
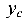) очевидны.
Моменты инерции сечения относительно главных центральных осей:
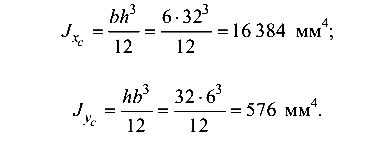
Эксцентриситет силы F в рассматриваемом сечении
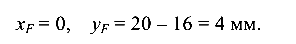
- Внутренние силы:
- продольная сила N = F = 20 кН;
- изгибающий момент относительно оси
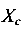
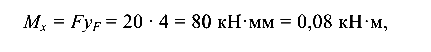
изгибающий момент относительно оси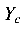 
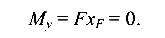
Поскольку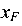 
= 0, а следовательно и 
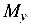= 0, здесь имеет место частный случай внецентренного растяжения (плоский изгиб). По формуле (8.5) определим положение нейтральной оси:
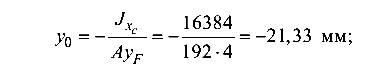
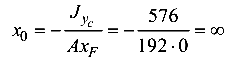(н.о. проходит параллельно оси ).
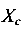Заметим, что нейтральная ось располагается по другую сторону от центра тяжести сечения, чем точка приложения силы F(pnc. 8.11, в).
Так как нейтральная ось проходит ниже сечения, не пересекая его, нормальные напряжения по всему сечению будут одного знака (растягивающие), но разные по абсолютному значению.
Определим нормальные напряжения в характерных точках сечения 3:
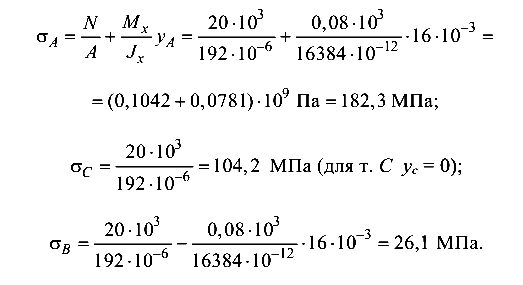
Как видно из результатов вычислений, нормальные напряжения наибольшие в точке, наиболее удаленной от нейтральной оси (точка А).
Эпюра нормальных напряжений для третьего сечения показана на рис. 8.11, в.
Условие прочности полосы обеспечено, так как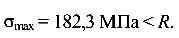 
Этот пример решения задачи взят со страницы решения задач с примерами по всем темам предмета «Сопротивление материалов»:
Примеры решения задач по сопротивлению материалов
Дополнительные задачи которые вам будут полезны:
