Оглавление:
Общий способ
Общее правило вычисления определённого интеграла заключается в применении формулы Ньютона — Лейбница. Для этого нужно найти первообразную и вычислить её приращение на интервале интегрирования.
Интегрирование по частям
Формула интегрирования по частям, применяемая в неопределённом интеграле, справедлива и для определённого интеграла со всеми рекомендациями по её применению. Различие заключается в том, что для найденной первообразной в определённом интеграле нужно найти её приращение.
Формула интегрирования по частям в определенном интеграле имеет вид:
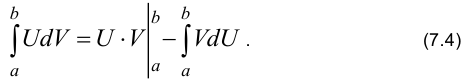
Пример №1:
Вычислить интеграл:
Интегрирование методом подстановки
Пусть для вычисления
определённого интеграла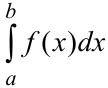 
применяется подстановка 
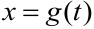. В этом случае пределы интегрирования изменяются, и их рассчитывают по формулам: 
. Справедливо равенство:
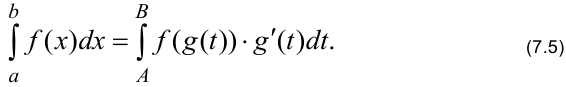
При использовании формулы (7.5) не нужно переходить к старой переменной интегрирования после определения первообразной, как это делается в неопределённом интеграле.
Пример №2:
Вычислить интеграл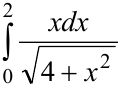 
.
Решение:
Обозначим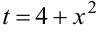 
, тогда 
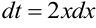. Пересчитаем пределы интеграла на новую переменную: при 
, при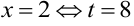 
. Запишем интеграл с новой переменной, предварительно умножив и разделив на 2:
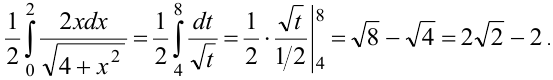
Пример №3:
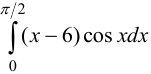
Решение:
Обозначим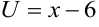 
, тогда 
. 
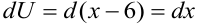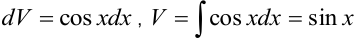. Подставим полученные выражения в формулу (7.4):
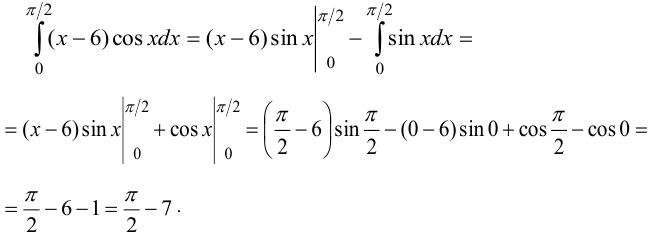
Вспомним, что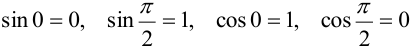 
. Кроме того, 
.
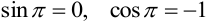Натуральный логарифм имеет значения: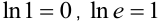 
.
Пример №4:
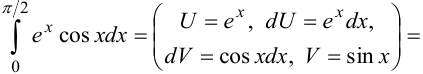
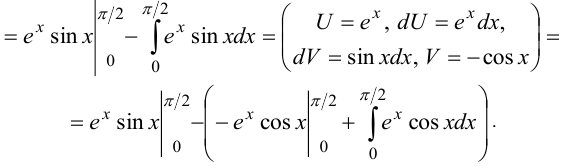
Таким образом, в левой и правой частях равенства стоят одинаковые интегралы:
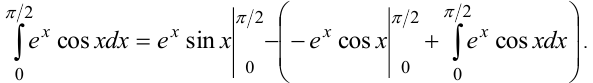
Перенесем интеграл из правой части в левую:
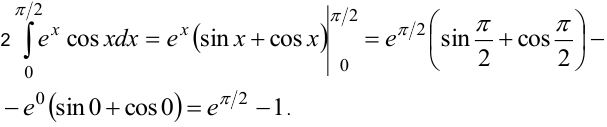
Окончательно,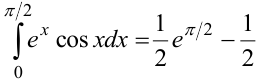 
.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
