Оглавление:
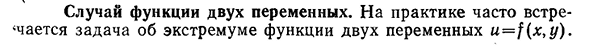



Случай функции двух переменных
- Для функций двух переменных. На практике часто возникает проблема экстремумов функции двух переменных u=f(x, y).§6. Локальные экстремумы 513 В этом параграфе мы покажем результаты для этого случая. d2y d2y d2y Является частной производной, которая
делает—— , ——- , —— в какой-то степени.- DH2ohdu DU2 ke L10 (x0, Uo) определяется символами AI, 012 и a2i соответственно. Функция двух переменных u=f (x, y) сделана так, чтобы иметь возможность дифференцировать один раз в окрестности точки
Mo и иметь возможность дифференцировать дважды в самой точке Mo, а MO Людмила Фирмаль
является стационарной точкой. Тогда, если условие apygg — «122>0» удовлетворяется точкой Mo, то функция u=f(x, y) имеет локальное экстремальное значение в точке Mo(максимум при AC<0,минимум при OC>0). Если точка Mo atsa22-ai22<0, то функция u=f (x, y) не имеет локальныхэкстремумов*в этой точке. * Случай а] 1022-А212=0 требует дальнейшего изучения. ** В этом случае p можно сделать меньше,
если это необходимо. Выполняется условие Y12+Y22=1. Д О К а з а т е л ь с т в о. эффективность первой части этого предложения непосредственно подчиняется критерию определения знака теоремы 12.16 и квадратичной форме Сильвестра L1=C, A2=aca22-ai22. Докажем вторую часть предложения. Таким образом, неравенство aca22-AI2<0 принимается истинным в точке Mo. В этом случае второй
- дифференциал d2u в МО оказывается знакопеременной формой. Используя приведенную выше нотацию, давайте сначала рассмотрим случай OC^O. P=/(X-X0) 2+ (//- Z / 0) 2 , Р Р Р Р Р Получаем следующее уравнение для второй производной: Два. d2u / m » =P2Y] aiffk = P2 (au / i? 4-Z a^h^+ai2h2}= i, k=\ — 4″ ^12^2)^ *4 (^11^22 ®12) Н2]. Привет, масло легко, пожалуйста, проверьте с hi=l, h2=0, LX= — — — — —, 1^0114-012 L2= — AC-дифференциал g/2i / M0-имеет другой знак. V4i+ » f2 является
знакопеременной формой, поэтому, согласно теореме 12.16, функция не имеет локальных экстремумов в МО. Зах 17 72514 гл. 12. Функции некоторых переменных Рассмотрим случай AC=0. Тогда условие apa2-aj22<<0 означает ai2#=0. Итак, как упоминалось выше, существует d2u|=p2h2(2a12hi+a22h2). Hi hi hi (12.85) пусть значение hi= £ 0 и h2 очень мало (условие hl2+h22=i, такой выбор hi и h2 возможен) выражение (2ai2hi+a22h2) содержит знак значения 2ai2hi.
Далее из уравнения (12.85) следует, что g/2Y|M0 имеет другой знак: Людмила Фирмаль
h2>0 и h2<0, то есть функция u=f(x, y) не имеет экстремального значения в L40. Это утверждение полностью доказано. Z a m e h a n I e. требования d2f(M0)>0 [соответствующие d2f(M0)<0] — это требование для локального минимума[максимума]в точке Mo функции f (M), которая дважды различается в этом отношении. В C a m o m d e, но имеющий локальный минимум в точке ui0 для определенности f(M), так что условие d 2 F (M o)^O не выполняется. Тогда есть привет, h2… Да такая штука МНТ 1=1k=l F (t)=f (xi°+thi,… хм°+тнм), четко определены для всех T и достаточно малых по модулю. Функция F (t) должна иметь локальный минимум точки 1=0, что противоречит условию F»(O)=d2f (M o)<O.
Смотрите также:
| Площадь криволинейной трапеции и криволинейного сектора | Понятие экстремума функции m переменных. Необходимые условия экстремума |
| Примеры вычисления площадей. | Производная по направлению. Градиент |

