Оглавление:
Курс лекций для студентов 1 курса по математическому анализу любых форм обучения. Я собрала теорию и примеры с решениями к каждой теме, чтобы вы смогли подготовиться к экзамену или освежить память перед контрольной работой!
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Введение в математический анализ
Математический анализ — совокупность разделов математики, посвящённых исследованию функций и их обобщений методами дифференциального и интегрального исчислений. При столь общей трактовке к анализу следует отнести и функциональный анализ вместе с теорией интеграла Лебега, комплексный анализ (ТФКП), изучающий функции, заданные на комплексной плоскости, нестандартный анализ, изучающий бесконечно малые и бесконечно большие числа, а также вариационное исчисление.
Функция. Предел функции
Математический анализ — раздел математики, в котором изучаются функции. В экономическом анализе часто исследуют, например, зависимости спроса и предложения от цены (функции спроса и предложения), зависимость издержек производства от объема продукции (функцию издержек) и др. Зависимость переменной у от переменной х называется функцией, если каждому элементу 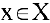 ставится в соответствие единственный элемент
ставится в соответствие единственный элемент 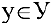 , обозначаемый
, обозначаемый 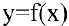 . При этом элементы
. При этом элементы 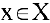 называются независимыми переменными (или аргументами), а элементы
называются независимыми переменными (или аргументами), а элементы 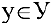 называются зависимыми переменными (или значениями функции). Множество X называют областью определения функции, а множество У — областью значений функции. Функция называется сложной (или композицией функций, или функцией от функций), если ее аргумент в свою очередь является функцией другой переменной:
называются зависимыми переменными (или значениями функции). Множество X называют областью определения функции, а множество У — областью значений функции. Функция называется сложной (или композицией функций, или функцией от функций), если ее аргумент в свою очередь является функцией другой переменной: 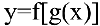 .
.
В школьном курсе изучались следующие функции: постоянная 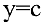
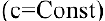 , степенная
, степенная 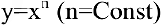 , показательная
, показательная 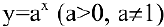 , логарифмическая
, логарифмическая 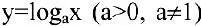 , тригонометрические
, тригонометрические 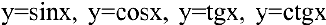 и обратные тригонометрические
и обратные тригонометрические 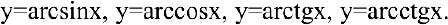 Все эти функции называются основными элементарными функциями. Функции, полученные с помощью конечного числа арифметических действий и образования сложных функций над основными элементарными функциями называются элементарными. Это класс функций, с которыми мы будем работать на протяжении всего курса.
Все эти функции называются основными элементарными функциями. Функции, полученные с помощью конечного числа арифметических действий и образования сложных функций над основными элементарными функциями называются элементарными. Это класс функций, с которыми мы будем работать на протяжении всего курса.
Возможно эта страница вам будет полезна:
| Предмет математический анализ |
Одним из основных понятий математического анализа является предел. Примерами применения понятия предела могут служить окружность как предел вписанных и описанных многоугольников при бесконечном увеличении числа сторон или касательная как предельное положение секущей при сближении точек пересечения. Говорят, что функция 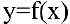 имеет предел А при х стремящемся к
имеет предел А при х стремящемся к 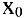 , если значения функции
, если значения функции 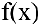 сколь угодно близко приближаются к числу А, когда значения переменной х сколь угодно близко приближаются к числу
сколь угодно близко приближаются к числу А, когда значения переменной х сколь угодно близко приближаются к числу 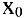 .
.
Используя логические символы: 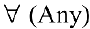 — «для любого»,
— «для любого», 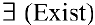 — «существует», символ равносильности
— «существует», символ равносильности 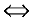 — «тогда и только тогда, когда», символ следствия
— «тогда и только тогда, когда», символ следствия  — «следует, что», и символ : — «такое, что», определение предела можно записать в виде:
— «следует, что», и символ : — «такое, что», определение предела можно записать в виде:
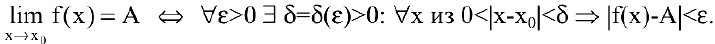
Внимание! Определение предела не требует существования функции в самой предельной точке 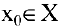 , т.к. рассматривает значения
, т.к. рассматривает значения 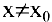 в некоторой окрестности точки
в некоторой окрестности точки 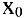 .
.
Если функция 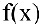 определена в некоторой точке
определена в некоторой точке 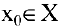 и в некоторой ее окрестности существует предел функции при
и в некоторой ее окрестности существует предел функции при 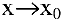 , равный значению функции в этой точке:
, равный значению функции в этой точке:
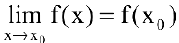
то функция 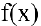 называется непрерывной в точке
называется непрерывной в точке 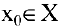 . Говорят, что функция непрерывна на множестве X, если она непрерывна в каждой точке этого множества.
. Говорят, что функция непрерывна на множестве X, если она непрерывна в каждой точке этого множества.
Следовательно, в случае непрерывных функций очень просто находятся пределы в любой точке области определения: для этого достаточно вычислить значение функции в данной точке.
Утверждение 1. Любая элементарная функция непрерывна в области определения.
Утверждение 2. Под знаком непрерывной функции можно переходить к пределу: 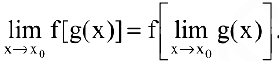
Пример №1
Вычислить предел 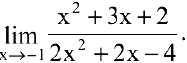
Решение:
Данная функция элементарная, т.к. получена из основных элементарных функций (постоянной и степенной) с помощью конечного числа арифметических действий. Поскольку 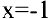 принадлежит области определения функции, то ее предел в точке
принадлежит области определения функции, то ее предел в точке 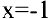 равен значению функции в этой точке, т.е.
равен значению функции в этой точке, т.е.
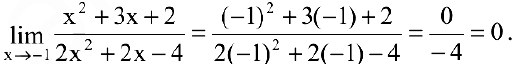
Заметим, что не всякий производственный процесс непрерывен во времени. Аргумент функции может изменяться лишь в отдельные моменты. Так, приняв за область определения функции множество натуральных чисел 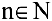 , получим функцию
, получим функцию 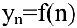 натурального аргумента, которую называют числовой последовательностью. Число
натурального аргумента, которую называют числовой последовательностью. Число 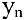 называют общим членом числовой последовательности. Например, арифметическая или геометрическая прогрессии — числовые последовательности.
называют общим членом числовой последовательности. Например, арифметическая или геометрическая прогрессии — числовые последовательности.
Число А называется пределом числовой последовательности 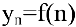 , если для любой окрестности точки А все члены последовательности, начиная с некоторого номера N, принадлежат этой окрестности. Обозначение:
, если для любой окрестности точки А все члены последовательности, начиная с некоторого номера N, принадлежат этой окрестности. Обозначение: 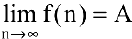 .
.
(Символ 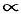 означает «бесконечно большую величину».)
означает «бесконечно большую величину».)
С понятием предела числовой последовательности тесно связано понятие предела функции на бесконечности, которое на языке логических символов имеет вид:
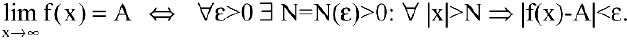
Замечание. Переменная 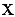 может неограниченно стремиться либо в сторону отрицательных значений:
может неограниченно стремиться либо в сторону отрицательных значений: 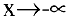 , либо в сторону положительных значений:
, либо в сторону положительных значений: 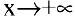 . Символ ос является объединением двух символов:
. Символ ос является объединением двух символов: 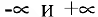 . Очевидно, что
. Очевидно, что
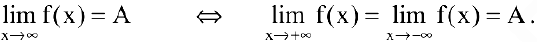
В общем случае если при стремлении 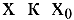 переменная
переменная 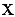 принимает лишь значения, меньшие
принимает лишь значения, меньшие 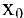 , и при этом функция
, и при этом функция 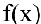 стремится к некоторому числу, то говорят о пределе функции слева:
стремится к некоторому числу, то говорят о пределе функции слева:
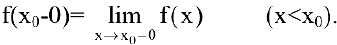
И наоборот, если при стремлении 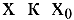 переменная х принимает лишь значения, большие
переменная х принимает лишь значения, большие 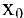 , и при этом функция f(x) стремится к некоторому числу, то говорят о пределе функции справа:
, и при этом функция f(x) стремится к некоторому числу, то говорят о пределе функции справа:
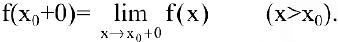
(При 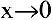 на практике вместо 0-0 пишут -0, а вместо 0+0 — +0.)
на практике вместо 0-0 пишут -0, а вместо 0+0 — +0.)
Если односторонние пределы различны или хотя бы один из них не существует, то не существует и предел функции в данной точке. Следовательно,
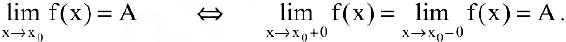
В следующем параграфе мы познакомимся с основными правилами вычисления пределов при х—»хо(ос).
Основные теоремы о пределах
Внимание! Если предел существует, то он единственный.
Теорема 1. Предел постоянной равен самой постоянной: 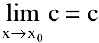 .
.
Теорема 2. Пусть 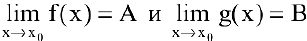 . Тогда:
. Тогда:
1) предел суммы конечного числа функций равен сумме пределов этих функций:
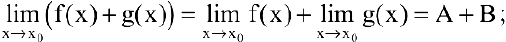
2) предел произведения конечного числа функций равен произведению пределов этих функций:
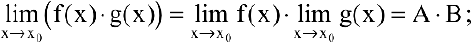
в частности, постоянный множитель можно выносить за знак предела:
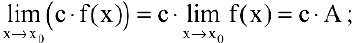
3) предел частного двух функций равен частному пределов этих функций при условии, что предел делителя не равен нулю:
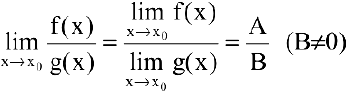
Возможно эта страница вам будет полезна:
| Решение задач по математическому анализу |
Пример №2
Вычислить предел 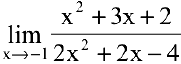
Решение:
Воспользовавшись теоремами о пределах частного, суммы и произведения, получим
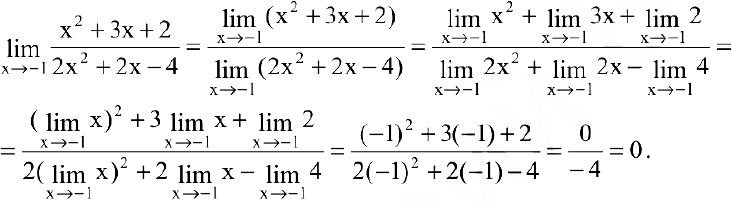
Пример №3
Вычислить предел последовательности
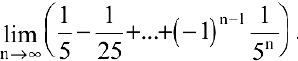
Решение:
Теорему о пределе суммы конечного числа функций здесь применить нельзя. Заметим, что 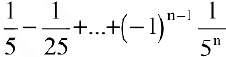 является суммой n первых членов геометрической прогрессии со знаменателем
является суммой n первых членов геометрической прогрессии со знаменателем 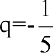 и первым членом
и первым членом 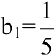 . Следовательно,
. Следовательно,
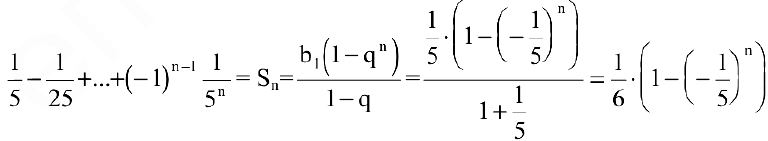
Тогда по теоремам о пределах функций имеем:
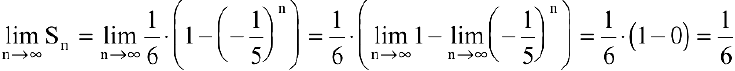
Рассмотрим соотношения пределов суммы, произведения, частного, распространенные на случай бесконечного предела функции.
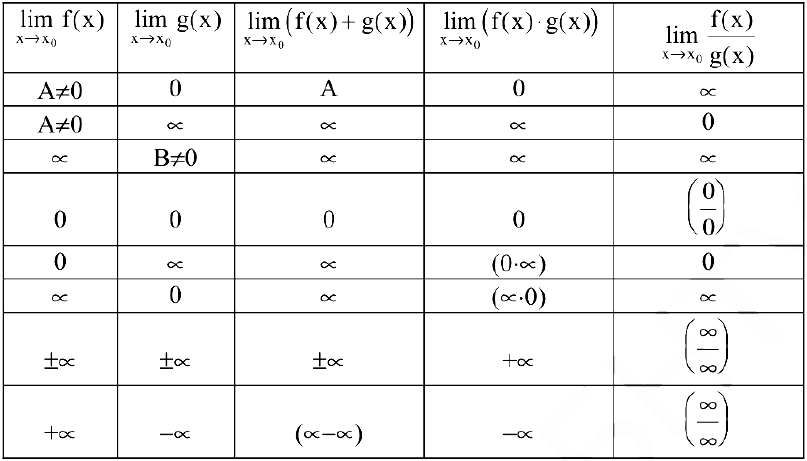
Если вычисление пределов приводит к неопределенным выражениям вида 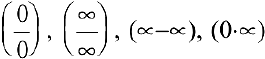 , необходимо провести дополнительные исследования, т.е. «раскрыть неопределенность».
, необходимо провести дополнительные исследования, т.е. «раскрыть неопределенность».
Раскрытие неопределенностей
Раскрытие неопределенностей вида 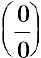 . Пусть
. Пусть 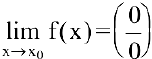 .
.
1. Если 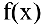 — рациональная дробь, то числитель и знаменатель дроби раскладывают на множители.
— рациональная дробь, то числитель и знаменатель дроби раскладывают на множители.
Пример №4
Вычислить предел 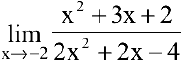
Решение:
Числитель и знаменатель дроби 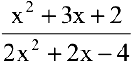 при
при 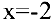 обращаются в нуль. Имеем неопределенность вида
обращаются в нуль. Имеем неопределенность вида 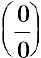 . Для ее раскрытия разложим числитель и знаменатель дроби на множители, а затем применим теоремы о пределах частного, суммы и произведения:
. Для ее раскрытия разложим числитель и знаменатель дроби на множители, а затем применим теоремы о пределах частного, суммы и произведения:
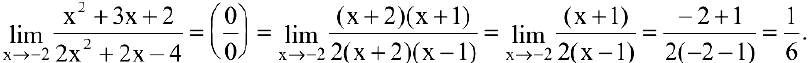
2. Если 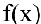 — дробь, содержащая иррациональные выражения, то выделение множителей вида
— дробь, содержащая иррациональные выражения, то выделение множителей вида 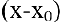 достигается переводом иррациональностей в числитель или знаменатель.
достигается переводом иррациональностей в числитель или знаменатель.
Пример №5
Вычислить предел 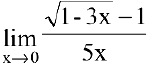 .
.
Решение:
Имеем неопределенность вида 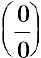 . Избавимся от иррациональности в числителе, умножив и разделив дробь на сопряженное к числителю выражение
. Избавимся от иррациональности в числителе, умножив и разделив дробь на сопряженное к числителю выражение 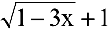 . Получим:
. Получим:
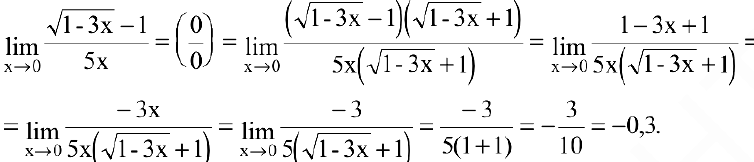
3. В остальных случаях для раскрытия неопределенности вида 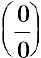 используют первый замечательный предел (см. п. 3.4) или эквивалентные бесконечно малые функции (см. п. 3.5).
используют первый замечательный предел (см. п. 3.4) или эквивалентные бесконечно малые функции (см. п. 3.5).
Раскрытие неопределенностей вида 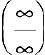 . Пусть
. Пусть 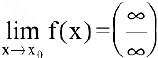
Если 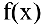 — рациональная дробь или дробь, содержащая иррациональности, то числитель и знаменатель делят на х в старшей степени.
— рациональная дробь или дробь, содержащая иррациональности, то числитель и знаменатель делят на х в старшей степени.
Пример №6
Вычислить предел 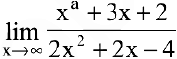 , если 1) а=2; 2) а— 1; 3) а=4.
, если 1) а=2; 2) а— 1; 3) а=4.
Решение:
Числитель и знаменатель дроби конечного предела не имеют. Имеем неопределенность вида  . Для ее раскрытия разделим числитель и знаменатель дроби на высшую степень
. Для ее раскрытия разделим числитель и знаменатель дроби на высшую степень 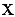 (в первом и втором случаях на
(в первом и втором случаях на 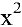 , во третьем — на
, во третьем — на 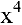 ), а затем воспользуемся теоремами о пределах функций:
), а затем воспользуемся теоремами о пределах функций:
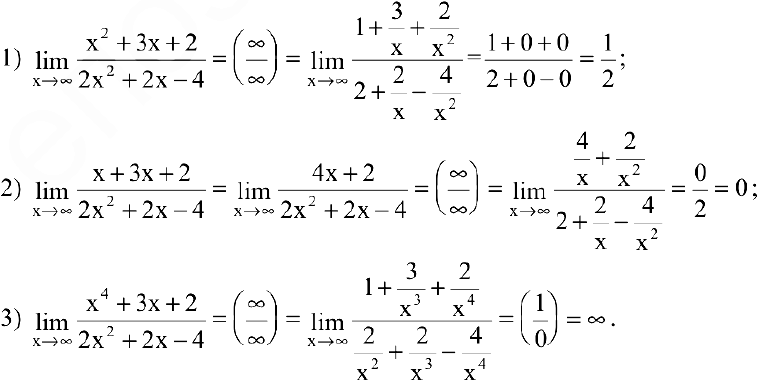
Вывод. Предел рациональной дроби на бесконечности равен отношению коэффициентов при старших степенях, если эти степени совпадают, нулю — если показатель степени числителя меньше показателя степени знаменателя и бесконечности в противном случае.
Замечание. Для раскрытия неопределенностей вида 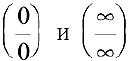 используют также правило Лопиталя (см. п. 3.8).
используют также правило Лопиталя (см. п. 3.8).
Раскрытие неопределенностей вида 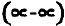 . Неопределенное выражение вида
. Неопределенное выражение вида 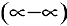 преобразуется к неопределенности вида
преобразуется к неопределенности вида 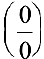 или
или  . Методику раскрытия такой неопределенности покажем на примерах.
. Методику раскрытия такой неопределенности покажем на примерах.
Пример №7
Вычислить предел 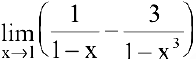 .
.
Решение:
Имеем неопределенность вида 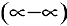 которая преобразуется к неопределенности вида
которая преобразуется к неопределенности вида 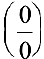 приведением функции к общему знаменателю:
приведением функции к общему знаменателю:
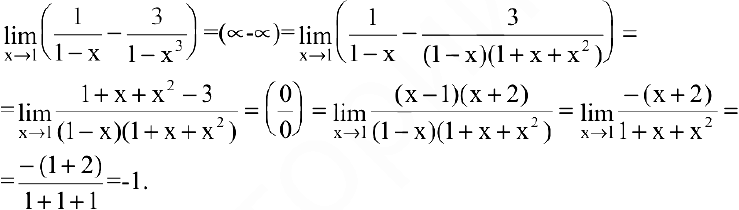
Пример №8
Вычислить предел последовательности
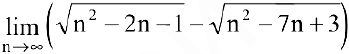
Решение:
Для раскрытия неопределенности вида 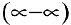 умножим и разделим выражение в скобках на сопряженное:
умножим и разделим выражение в скобках на сопряженное:
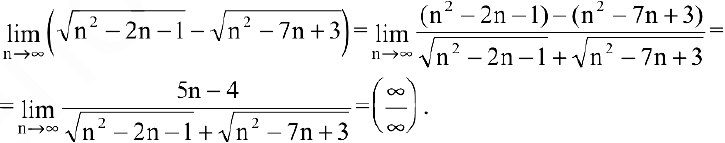
Получили неопределенность вида  . Раскроем ее, разделив все члены полученного выражения на n:
. Раскроем ее, разделив все члены полученного выражения на n:
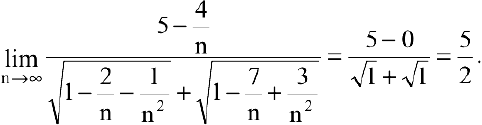
Раскрытие неопределенностей вида 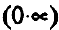 . Неопределенное выражение вида
. Неопределенное выражение вида 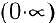 получается при нахождении пределов вида
получается при нахождении пределов вида 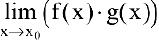 , где
, где 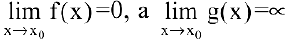 , и сводится к неопределенности вида
, и сводится к неопределенности вида 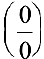 или
или  следующим образом:
следующим образом:
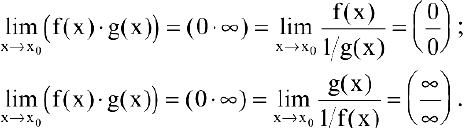
Замечание. При вычислении пределов показательно-степенных функций 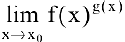 могут получиться неопределенности вида
могут получиться неопределенности вида 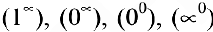 , для раскрытия которых используют второй замечательный предел или правило Ло-питаля.
, для раскрытия которых используют второй замечательный предел или правило Ло-питаля.
Замечательные пределы
Первый замечательный предел. Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен единице:
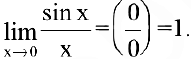
Следовательно,
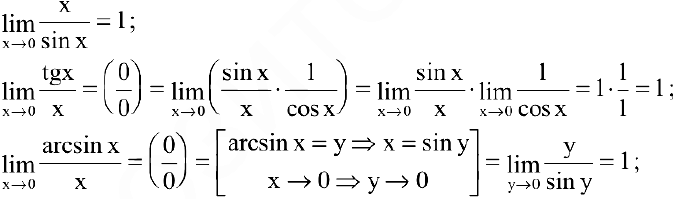
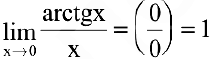 (аналогично).
(аналогично).
Возможно эта страница вам будет полезна:
| Методическое пособие по математическому анализу |
Пример №9
Найти 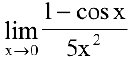
Решение:
Применим первый замечательный предел:
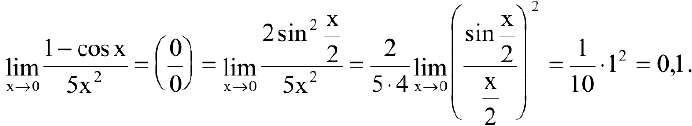
Второй замечательный предел. Числом е называется предел функции 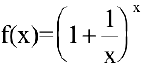 при
при 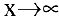 :
:
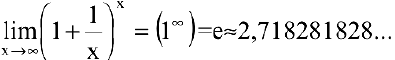
(Для запоминания: 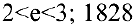 — год рождения Л.Н. Толстого) Следовательно,
— год рождения Л.Н. Толстого) Следовательно,
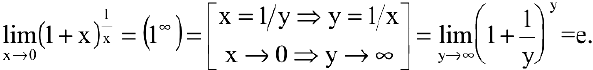
Задача о непрерывном начислении процентов. Первоначальный вклад в банк составил 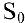 денежных единиц. Банк выплачивает ежегодно
денежных единиц. Банк выплачивает ежегодно 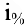 годовых. Необходимо найти размер вклада
годовых. Необходимо найти размер вклада 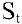 через
через 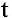 лет.
лет.
Решение:
Размер вклада будет увеличиваться ежегодно в 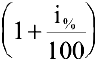 раз и через
раз и через 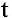 лет составит
лет составит 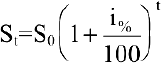 . Если же начислять проценты n раз в году, то будущая сумма составит
. Если же начислять проценты n раз в году, то будущая сумма составит 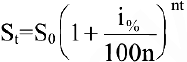 . Предположим, что проценты по вкладу начисляются каждое полугодие
. Предположим, что проценты по вкладу начисляются каждое полугодие 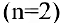 , ежеквартально
, ежеквартально 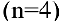 , ежемесячно
, ежемесячно 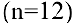 , каждый день
, каждый день 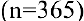 , каждый час
, каждый час 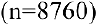 и, наконец, непрерывно
и, наконец, непрерывно 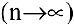 . Тогда за год размер вклада составит:
. Тогда за год размер вклада составит:
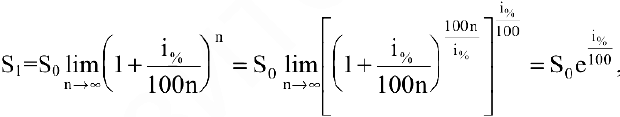
а за 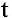 лет:
лет:
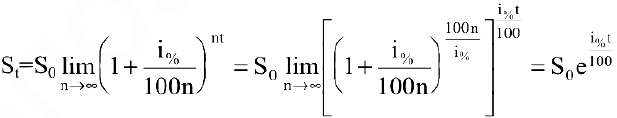
Пример №10
Найти 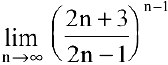
Решение:
Т.к. 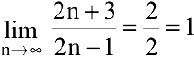 , имеем неопределенность вида
, имеем неопределенность вида 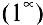 . Для ее раскрытия воспользуемся вторым замечательным пределом, выделив предварительно у дроби целую часть:
. Для ее раскрытия воспользуемся вторым замечательным пределом, выделив предварительно у дроби целую часть:
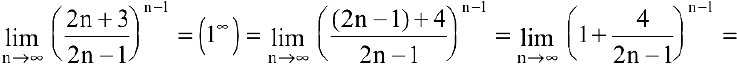
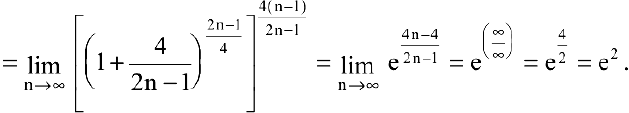
Пример №11
Найти 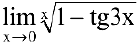 .
.
Решение:
Преобразуя выражение и используя непрерывность показательно-степенной функции, получим:
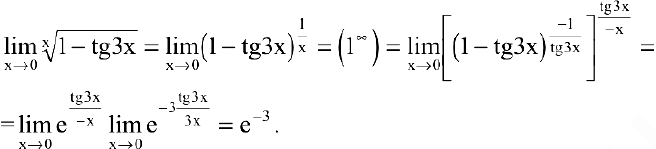
Бесконечно малые и бесконечно большие функции
Математическая интерпретация явления часто заключается в том, что практически очень малые величины принимаются за бесконечно малые. Так, рассматривая годовое производство, мы можем отдельный день представить себе как бесконечно малую частицу годового периода и получать при этом практически верные результаты.
Функция 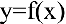 называется бесконечно малой при
называется бесконечно малой при 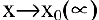 , если ее предел равен нулю:
, если ее предел равен нулю: 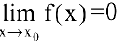 .
.
Функция 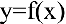 называется бесконечно большой при
называется бесконечно большой при 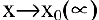 , если ее предел равен бесконечности:
, если ее предел равен бесконечности: 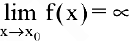 .
.
Между бесконечно малыми и бесконечно большими функциями существует связь: если 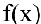 — бесконечно малая функция при
— бесконечно малая функция при 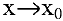 , то
, то 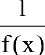 бесконечно большая функция при
бесконечно большая функция при 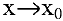 и наоборот.
и наоборот.
Теорема 1. Алгебраическая сумма и произведение конечного числа бесконечно малых функций при 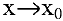 есть бесконечно малая функция при
есть бесконечно малая функция при 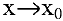 .
.
Теорема 2. Произведение бесконечно малой при 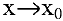 функции на ограниченную есть бесконечно малая функция при
функции на ограниченную есть бесконечно малая функция при 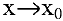 .
.
Возможно эта страница вам будет полезна:
| Математический анализ помощь онлайн |
Пример №12
Найти 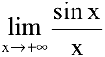 .
.
Решение:
Т.к. 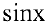 — ограниченная функция для любых
— ограниченная функция для любых 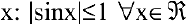 , а
, а  — бесконечно малая функция при
— бесконечно малая функция при 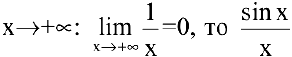 — бесконечно малая функция при
— бесконечно малая функция при 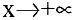 , т.е.
, т.е. 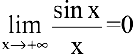 .
.
Если 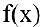 и
и 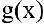 — бесконечно малые функции при
— бесконечно малые функции при 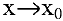 , то
, то 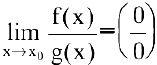 может быть равен либо нулю, либо бесконечности, либо какому-нибудь числу, отличному от нуля; наконец, предел может не существовать.
может быть равен либо нулю, либо бесконечности, либо какому-нибудь числу, отличному от нуля; наконец, предел может не существовать.
Если 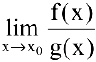 не существует, то
не существует, то 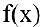 и
и 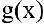 называют несравнимыми бесконечно малыми при
называют несравнимыми бесконечно малыми при 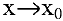 .
.
Если 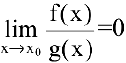 , то функция
, то функция 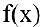 стремится к нулю быстрее, чем
стремится к нулю быстрее, чем 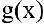 при
при 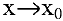 . Говорят, что
. Говорят, что 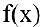 — бесконечно малая более высокого порядка, чем
— бесконечно малая более высокого порядка, чем 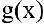 при
при 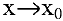 и пишут:
и пишут: 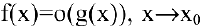 (читается «
(читается «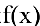 есть о малое от
есть о малое от 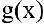 при
при 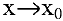 ).
).
Если 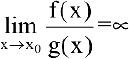 , то
, то 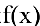 называют бесконечно малой более низкого порядка, чем
называют бесконечно малой более низкого порядка, чем 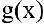 при
при 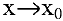 и пишут:
и пишут: 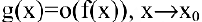 .
.
Если 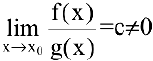 , то
, то 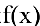 и
и 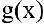 называют бесконечно малыми одного порядка при
называют бесконечно малыми одного порядка при 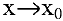 и пишут:
и пишут: 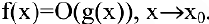 .
.
Особенно важен частный случай, когда 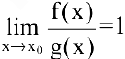 . Тогда
. Тогда 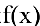 и
и 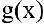 называют эквивалентными бесконечно малыми при
называют эквивалентными бесконечно малыми при 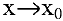 и пишут:
и пишут: 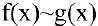 ,
, 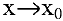 .
.
Пример №13
Показать, что 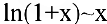 при
при 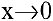 .
.
Решение:
Функции 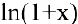 и
и 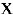 являются бесконечно малыми
являются бесконечно малыми 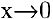 . Найдем предел их отношения
. Найдем предел их отношения 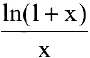 при
при 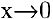 :
:
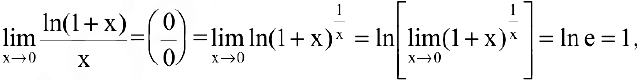
что и требовалось доказать.
Переход к пределу под символом логарифма возможен, т.к. логарифмическая функция непрерывна.
Утверждение. Если 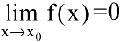 , то при
, то при 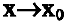 следующие функции эквивалентны:
следующие функции эквивалентны:
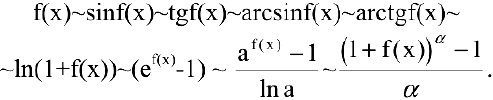
Данная цепочка эквивалентностей используется при нахождении пределов.
Теорема 3. Предел отношения двух бесконечно малых функций не изменится, если эти бесконечно малые заменить им эквивалентными.
Пример №14
Вычислить предел 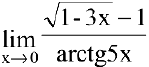 .
.
Решение:
Для нахождения предела используем свойства эквивалентности бесконечно малых функций:
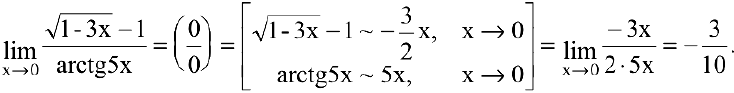
Пример №15
Вычислить предел 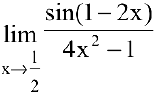 .
.
Решение:
Используя теорему об эквивалентных бесконечно малых, получаем:
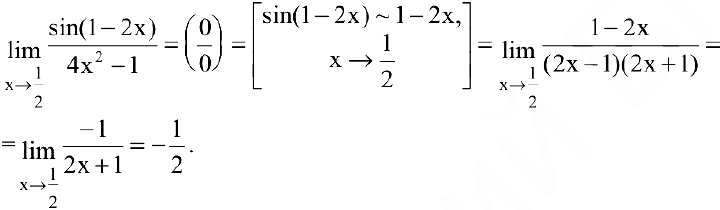
Точки разрыва и их классификация
Непрерывность или разрыв функции может зависеть от конкретных условий, в которых рассматривается задача. Рассмотрим, например, численность населения земного шара как функцию времени. Она увеличивается на 1 в момент рождения каждого человека и уменьшается на 1 в момент смерти. Но рождения и смерти следуют друг за другом через бесконечно малые интервалы времени и изменение численности населения планеты на 1 настолько мало его меняет, что практически функцию можно рассматривать непрерывной. Но стоит перейти от численности населения земного шара к численности населения одной квартиры, как рождение или смерть отдельного ее жителя будут так заметно менять ее численность, что функцию нельзя будет рассматривать как непрерывную.
Если хотя бы одно из условий определения непрерывности функции в точке (см. п. 3.1) не выполнено, то в данной точке функция терпит разрыв. Различают три вида точек разрыва непрерывной функции.
1. Точка 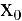 называется точкой устранимого разрыва функции
называется точкой устранимого разрыва функции 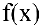 , если предел
, если предел 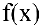 при
при 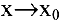 существует, но не равен значению функции в данной точке, т.е.
существует, но не равен значению функции в данной точке, т.е.
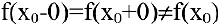
Чтобы устранить разрыв в точке 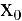 достаточно положить
достаточно положить 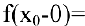
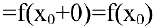 . В этом случае говорят, что функция доопределена до непрерывной в точке
. В этом случае говорят, что функция доопределена до непрерывной в точке 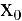 .
.
2. Точка Хо называется точкой разрыва первого рода функции 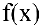 , если в этой точке функция
, если в этой точке функция 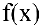 имеет конечные пределы слева
имеет конечные пределы слева 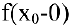 и справа
и справа 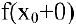 , не равные друг другу:
, не равные друг другу:
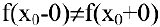
При этом величина 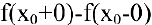 называется скачком функции
называется скачком функции 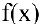 в точке
в точке 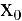 .
.
3. Если хотя бы один из односторонних пределов 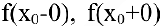 равен бесконечности или не существует, то
равен бесконечности или не существует, то 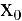 называется точкой разрыва второго рода функции
называется точкой разрыва второго рода функции 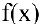 .
.
Пример №16
Исследовать функции на непрерывность. В случае устранимого разрыва доопределить функцию до непрерывной.
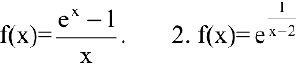
Решение:
1. Данная функция элементарная, т.к. получена с помощью конечного числа арифметических действий над основными элементарными функциями: экспоненциальной, постоянной и степенной. Следовательно, она непрерывна в области определения 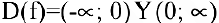 . При
. При 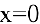 функция
функция 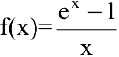 не определена и поэтому разрывна. Исследуем характер точки разрыва. Так как
не определена и поэтому разрывна. Исследуем характер точки разрыва. Так как
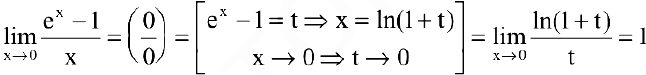
тo 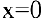 — точка устранимого разрыва.
— точка устранимого разрыва.
Если положить 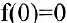 , то функция
, то функция
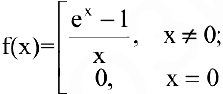
будет непрерывной для всех х.
2. Функция 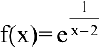 является элементарной как композиция основных элементарных функций. Следовательно, она непрерывна в области определения
является элементарной как композиция основных элементарных функций. Следовательно, она непрерывна в области определения 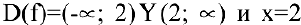 — точка разрыва. Для исследования характера точки разрыва найдем односторонние пределы:
— точка разрыва. Для исследования характера точки разрыва найдем односторонние пределы:
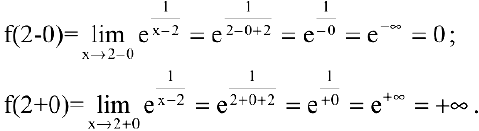
Так как один из односторонних пределов равен бесконечности, то 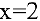 -точка разрыва второго рода.
-точка разрыва второго рода.
Пример №17
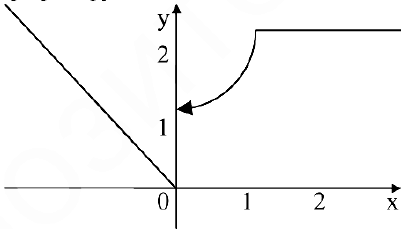
Исследовать функцию на непрерывность. Построить схематично график функции.
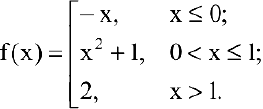
Решение:
Область определения этой функции — вся числовая прямая: 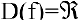 . Однако функция является составной. Составляющие ее функции непрерывны на множестве действительных чисел как элементарные. Поскольку функция задана различными аналитическими выражениями, то проверить на непрерывность нужно точки «стыка»
. Однако функция является составной. Составляющие ее функции непрерывны на множестве действительных чисел как элементарные. Поскольку функция задана различными аналитическими выражениями, то проверить на непрерывность нужно точки «стыка» 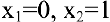 . Исследуем точку
. Исследуем точку 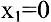 :
:
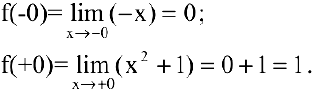
Так как 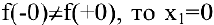 — точка разрыва первого рода. Скачок функции в данной точке равен
— точка разрыва первого рода. Скачок функции в данной точке равен 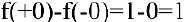 .
.
Исследуем точку 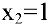 :
:
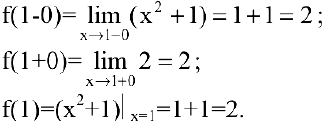
Поскольку 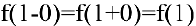 , то в точке
, то в точке 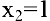 функция непрерывна. Следовательно, искомая функция непрерывна для всех
функция непрерывна. Следовательно, искомая функция непрерывна для всех 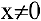 .
.
Построим график функции.
Дифференциальное исчисление
Производная функции, ее геометрический и физический смыслы
При изучении различных экономических процессов, описываемых функциями, существенную роль играют скорость роста процесса, ускорение роста, оптимальный режим и другие характеристики, которые исследуются с помощью производной.
Рассмотрим геометрическую задачу о проведении касательной к плоской кривой. Пусть на плоскости 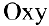 дана непрерывная кривая
дана непрерывная кривая 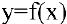 . Необходимо найти уравнение касательной к этой кривой в точке
. Необходимо найти уравнение касательной к этой кривой в точке 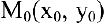 . Уравнение прямой, проходящей через точку
. Уравнение прямой, проходящей через точку 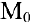 , имеет вид:
, имеет вид:
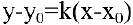
Касательной называется прямая, к которой стремится секущая при стремлении второй точки секущей к первой. Дадим аргументу 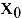 приращение
приращение 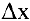 и перейдем на кривой
и перейдем на кривой 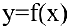 от точки
от точки 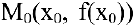 к точке
к точке 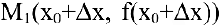 . Угловой коэффициент (или тангенс угла наклона) секущей
. Угловой коэффициент (или тангенс угла наклона) секущей 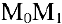 может быть найден по формуле:
может быть найден по формуле:
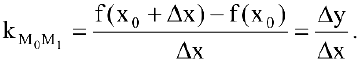
Тогда угловой коэффициент касательной
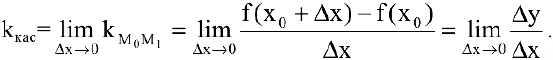
Это и есть производная функции 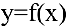 в точке
в точке 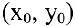 . Таким образом, угловой коэффициент касательной к графику функции равен значению ее производной в точке касания (геометрический смысл производной).
. Таким образом, угловой коэффициент касательной к графику функции равен значению ее производной в точке касания (геометрический смысл производной).
Производная функции имеет несколько обозначений:
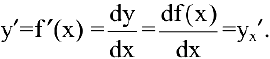
Следовательно, уравнение касательной к кривой 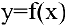 в точке
в точке 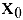 можно записать в виде:
можно записать в виде:
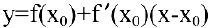
Нахождение мгновенной скорости прямолинейно движущейся точки. Пусть точка М движется прямолинейно и 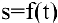 — путь, проходимый ею за время
— путь, проходимый ею за время 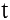 . Средней скоростью прямолинейного движения за время
. Средней скоростью прямолинейного движения за время 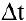 называется от-ношение пройденного пути к затраченному времени:
называется от-ношение пройденного пути к затраченному времени: 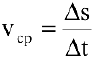 . Если существует предел
. Если существует предел 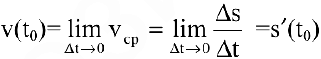 , то он называется (мгновенной) скоростью в некоторый момент времени
, то он называется (мгновенной) скоростью в некоторый момент времени 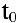 . В этом состоит физический смысл производной.
. В этом состоит физический смысл производной.
Если 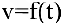 — функция, описывающая процесс изменения скорости неравномерного движения в зависимости от времени
— функция, описывающая процесс изменения скорости неравномерного движения в зависимости от времени 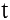 , то (мгновенное) ускорение материальной точки в фиксированный момент времени
, то (мгновенное) ускорение материальной точки в фиксированный момент времени 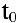 есть производная от скорости по времени:
есть производная от скорости по времени: 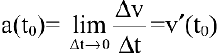 .
.
Вывод. Производная есть предел отношения приращения функции к бесконечно малому приращению аргумента.
Важно отметить, что запись 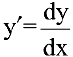 имеет не только символическое значение как способ написания производной, но и смысловое: производная функции есть отношение ее дифференциала
имеет не только символическое значение как способ написания производной, но и смысловое: производная функции есть отношение ее дифференциала 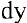 к дифференциалу аргумента
к дифференциалу аргумента  .
.
Дифференциалом функции одной переменной называется произведение ее производной на приращение аргумента: 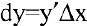 . Для функции
. Для функции 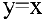 получаем
получаем 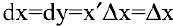 . Следовательно, дифференциал независимой переменной равен приращению этой переменной. Отсюда
. Следовательно, дифференциал независимой переменной равен приращению этой переменной. Отсюда 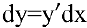 (подробнее см. литературу).
(подробнее см. литературу).
Нахождение для заданной функции ее производной называется дифференцированием данной функции. А учение о производной и ее приложениях является предметом дифференциального исчисления. Фундамент дифференциального исчисления составляют основные правила и формулы дифференцирования функций. Используя их, можно найти производную и дифференциал любой элементарной функции.
Основные правила дифференцирования
Внимание! Для существования производной в некоторой точке необходимо, чтобы функция была непрерывна в этой точке. Однако не всякая непрерывная в точке функция имеет в ней производную.
Теорема 1. Производная постоянной равна нулю: 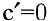 .
.
Теорема 2. Пусть 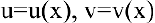 — дифференцируемые функции. Тогда:
— дифференцируемые функции. Тогда:
1) производная суммы конечного числа дифференцируемых функций равна сумме производных этих функций:
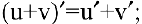
2) производная произведения конечного числа дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные:
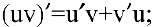
в частности, постоянный множитель можно выносить за знак производной:
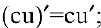
3) производная частного двух дифференцируемых функций может быть найдена по формуле:
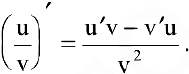
Теорема 3. Производная сложной функции равна ее производной по промежуточному аргументу, умноженной на производную промежуточного аргумента.
Действительно, пусть задана сложная функция 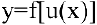 . Тогда
. Тогда
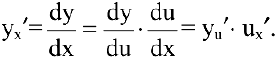
Теорема 4. Производная обратной функции есть величина, обратная производной прямой функции.
Так, если 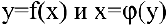 — взаимно обратные функции и
— взаимно обратные функции и 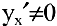 , то
, то 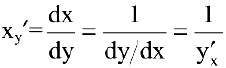
Таблица производных
Приведем основные формулы дифференцирования функций. Пусть 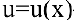 ~ дифференцируемая функция. Тогда
~ дифференцируемая функция. Тогда

Выведем производные некоторых функций.
1. Если 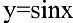 , то
, то
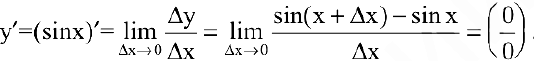
Используя формулу разности синусов
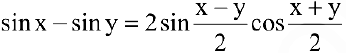
получим
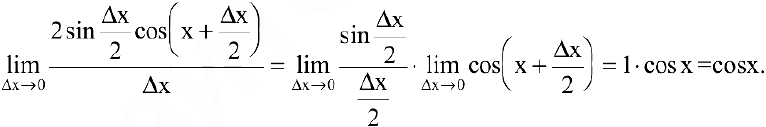
Так как любую тригонометрическую функцию можно вывести через синус, то нетрудно найти производные остальных тригонометрических функций.
2. Пусть 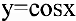 . Тогда по теореме о производной сложной функции
. Тогда по теореме о производной сложной функции
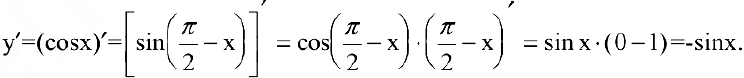
3. Для функции 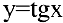 воспользуемся правилом дифференцирования частного:
воспользуемся правилом дифференцирования частного:
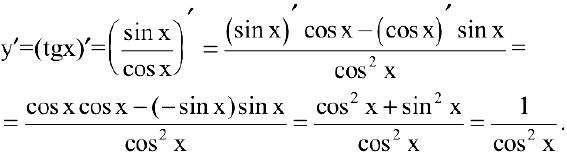
4. Представим 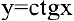 как степенную функцию от тангенса. Тогда
как степенную функцию от тангенса. Тогда
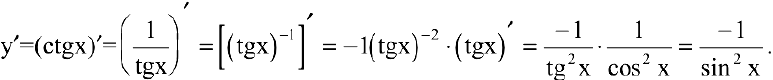
5. Вычислим производную 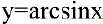 , где
, где 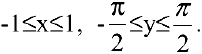 . Обратная функция имеет вид
. Обратная функция имеет вид 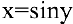 . Причем
. Причем 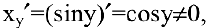 , если
, если 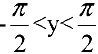 теореме дифференцирования обратной функции
теореме дифференцирования обратной функции
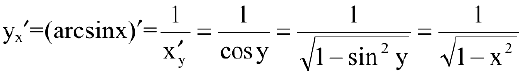
и при 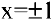 производная не существует.
производная не существует.
6. Производную 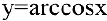 получим из соотношения
получим из соотношения 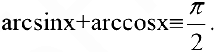 Следовательно,
Следовательно,
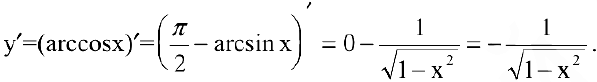
Предельный анализ в экономике
Задача о производительности труда. Пусть функция 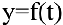 выражает количество произведенной продукции у за время
выражает количество произведенной продукции у за время 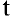 и необходимо найти производительность труда в момент времени
и необходимо найти производительность труда в момент времени 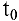 . Очевидно, за период времени от
. Очевидно, за период времени от 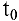 до
до 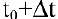 количество произведенной продукции изменится от
количество произведенной продукции изменится от 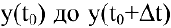 и составит
и составит 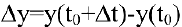 .
.
Средней производительностью труда называется отношение количества произведенной продукции к затраченному времени, т.е.
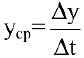
Производительность труда в момент времени 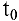 можно определить как предельное значение средней производительности за период времени от
можно определить как предельное значение средней производительности за период времени от 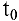 до
до 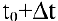 при
при 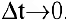 , т.е.
, т.е.
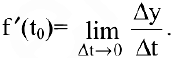
Возможно эта страница вам будет полезна:
| Сборники и решебники задач по математическому анализу |
Пример №18
Объем продукции хлебобулочных изделий, произведенных бригадой пекарей в течение смены, может быть описан функцией
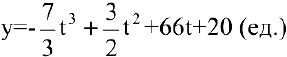
где 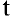 — время в часах. Вычислить производительность труда через час после начала работы.
— время в часах. Вычислить производительность труда через час после начала работы.
Решение:
Производительность труда выражается производной
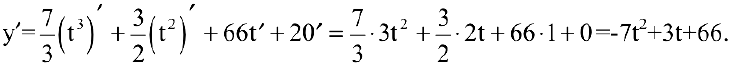
В заданный момент времени соответственно имеем:
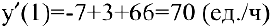
Задача о предельных издержках производства. Издержки производства у будем рассматривать как функцию количества выпускаемой продукции 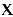 . Тогда
. Тогда 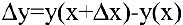 — приращение издержек производства с увеличением объема произведенной продукции на
— приращение издержек производства с увеличением объема произведенной продукции на 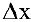 . Среднее приращение издержек производства на единицу продукции есть
. Среднее приращение издержек производства на единицу продукции есть 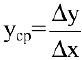 . Производная
. Производная 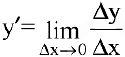 выражает предельные издержки производства и характеризует приближенно дополнительные затраты на производство единицы дополнительной продукции.
выражает предельные издержки производства и характеризует приближенно дополнительные затраты на производство единицы дополнительной продукции.
Аналогичным образом могут быть определены предельная выручка, предельный доход, предельная полезность и другие предельные величины.
Таким образом, производная выступает как скорость изменения некоторого экономического процесса во времени или относительно исследуемого фактора.
Для исследования экономических процессов часто используется понятие эластичности функции. Эластичностью функции 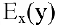 называется предел отношения относительного приращения функции к относительному приращению переменной, если приращение переменной стремится к нулю:
называется предел отношения относительного приращения функции к относительному приращению переменной, если приращение переменной стремится к нулю:
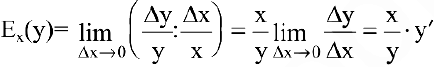
Эластичность дает приближенный процентный прирост функции при изменении независимой переменой на 1%. Например, эластичность спроса у относительно цены х показывает приближенно, на сколько процентов изменится спрос при изменении цены на 1%. Если эластичность спроса по абсолютной величине больше единицы 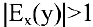 , то спрос считают эластичным, если
, то спрос считают эластичным, если 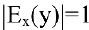 — нейтральным, если
— нейтральным, если 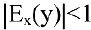 — неэластичным относительно цены.
— неэластичным относительно цены.
Пример №19
Опытным путем установлены функции спроса 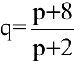 и предложения
и предложения 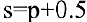 , где
, где 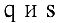 — количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени,
— количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени, 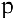 — цена товара. Найти:
— цена товара. Найти:
1) равновесную цену, при которой спрос и предложение совпадают;
2) эластичность спроса и предложения для этой цены;
3) изменение дохода при увеличении цены на 5% от равновесной.
Решение:
1) равновесная цепа определяется из условия 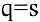 :
:
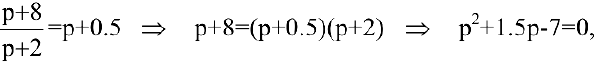
откуда 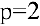 ден. ед.
ден. ед.
2) найдем эластичности спроса и предложения:
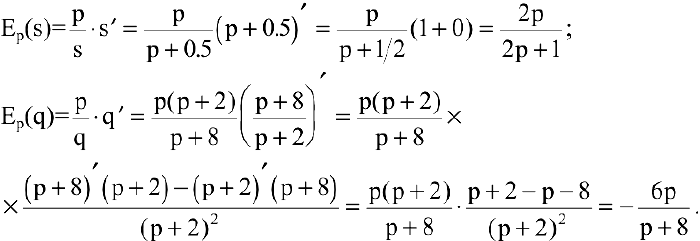
Для равновесной цены 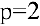 имеем:
имеем:
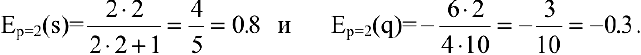
T.к. полученные значения эластичности по абсолютной величине меньше 1, то спрос и предложение данного товара при рыночной цене неэластичны относительно цены. Это означает, что изменение цены не приведет к резкому изменению спроса и предложения. А именно, при увеличении цены на 1% спрос уменьшится на 0.3%, предложение увеличится на 0.8%.
3) при увеличении цены на 5% относительно равновесной спрос уменьшится па (5-0.3)%= 1.5%, и, следовательно, доход возрастет па 3.5%.
Пример №20
Зависимость между издержками производства у и объемом выпускаемой продукции 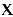 выражается функцией
выражается функцией 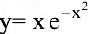 . Требуется:
. Требуется:
1) определить средние и предельные издержки при объеме продукции 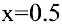 условных единиц;
условных единиц;
2) найти эластичность издержек при выпуске продукции, равном 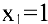 и
и 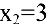 условных единиц.
условных единиц.
Решение:
1) функция средних издержек (на единицу продукции) выражается отношением
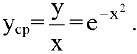
При 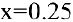 средние издержки равны
средние издержки равны
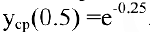
Функция предельных издержек выражается производной
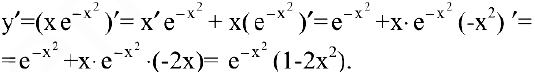
При 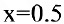 предельные издержки составят
предельные издержки составят
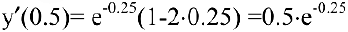
что вдвое меньше средних издержек.
2) эластичность издержек у относительно объема выпускаемой продукции х рассчитывается по формуле:
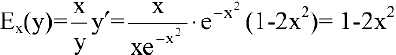
При 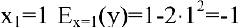 . Это означает, что при увеличении количества произведенной продукции на 1% (с 1 до 1.01) издержки уменьшатся на 1%.
. Это означает, что при увеличении количества произведенной продукции на 1% (с 1 до 1.01) издержки уменьшатся на 1%.
При 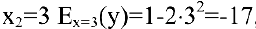 , т.е. с увеличением количества произведенной продукции на 1% (с 3 до 3.01) затраты уменьшатся на 17%.
, т.е. с увеличением количества произведенной продукции на 1% (с 3 до 3.01) затраты уменьшатся на 17%.
Уравнение нормали к плоской кривой
Нормалью называется прямая, проходящая через точку касания перпендикулярно касательной. Если касательная в точке 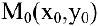 к графику непрерывной функции
к графику непрерывной функции 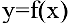 имеет вид
имеет вид 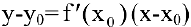 (см. п. 4.1), то перпендикулярная к ней прямая имеет угловой коэффициент
(см. п. 4.1), то перпендикулярная к ней прямая имеет угловой коэффициент
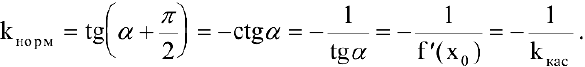
Таким образом, при 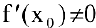 уравнение нормали в точке
уравнение нормали в точке 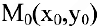 имеет вид
имеет вид
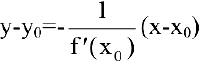
Если же 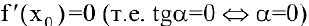 , то нормаль параллельна оси
, то нормаль параллельна оси 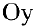 :
:
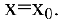
Задача. Показать, что для гиперболы 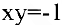 площадь треугольника, образованного координатными осями и касательной в точке
площадь треугольника, образованного координатными осями и касательной в точке 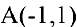 , равна квадрату полуоси гиперболы.
, равна квадрату полуоси гиперболы.
Решение:
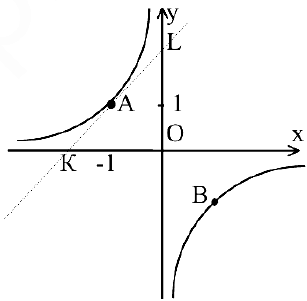
В общем курсе аналитической геометрии давалось каноническое уравнение гиперболы. «Школьная» гипербола 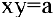 получается из уравнения
получается из уравнения 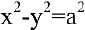 преобразованием поворота, которое нашей программой не предусмотрено. Полуось гиперболы определим как расстояние между вершиной и центром симметрии гиперболы. Очевидно, вершины гиперболы
преобразованием поворота, которое нашей программой не предусмотрено. Полуось гиперболы определим как расстояние между вершиной и центром симметрии гиперболы. Очевидно, вершины гиперболы 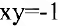 находятся в точках
находятся в точках 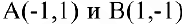 , а центр симметрии совпадает с началом координат. Тогда полуось гиперболы равна
, а центр симметрии совпадает с началом координат. Тогда полуось гиперболы равна 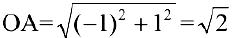 . Следовательно, квадрат полуоси гиперболы равен 2.
. Следовательно, квадрат полуоси гиперболы равен 2.
Составим уравнение касательной к гиперболе 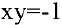 в вершине
в вершине 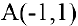 . Общее уравнение касательной к кривой
. Общее уравнение касательной к кривой 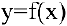 в точке
в точке 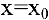 имеет вид:
имеет вид:
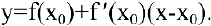
В нашем случае
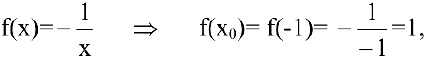
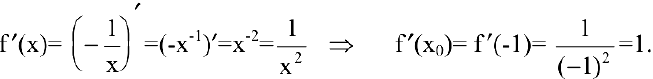
Искомое уравнение касательной имеет вид:

Найдем точки пересечения касательной с осями координат:
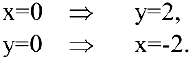
Тогда треугольник, образованный координатными осями и касательной, будет иметь вершины 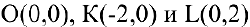 . Т.к. треугольник прямоугольный, то его площадь равна
. Т.к. треугольник прямоугольный, то его площадь равна
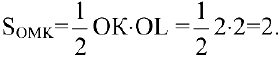
2=2. Задача решена.
Производные высших порядков
До сих пор мы рассматривали производную 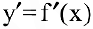 от функции
от функции 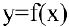 , называемую производной первого порядка. Но производная
, называемую производной первого порядка. Но производная 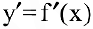 сама является функцией, которая также может иметь производную. Производной второго порядка называется производная от производной первого порядка
сама является функцией, которая также может иметь производную. Производной второго порядка называется производная от производной первого порядка 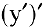 и обозначается
и обозначается 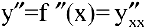 и т.д. В общем случае, производной n-го порядка называется производная от производной
и т.д. В общем случае, производной n-го порядка называется производная от производной 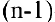 -ro порядка (для обозначения производных выше третьего порядка используются арабские цифры в скобках):
-ro порядка (для обозначения производных выше третьего порядка используются арабские цифры в скобках): 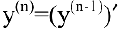 .
.
Ранее было установлено, что если точка движется прямолинейно по закону 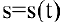 (где s — путь, t — время), то
(где s — путь, t — время), то 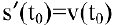 представляет скорость изменения пути в момент
представляет скорость изменения пути в момент 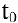 . Следовательно, ускорение точки в момент
. Следовательно, ускорение точки в момент 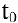 есть вторая производная пути по времени:
есть вторая производная пути по времени:
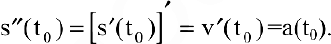
В этом состоит механический смысл второй производной.
Задача. Известно, что траекторией брошенного камня является парабола. Найти его скорость и ускорение.
Решение:
Запишем уравнение траектории брошенного камня 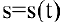 :
:
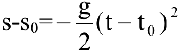 — парабола с вершиной в точке
— парабола с вершиной в точке 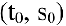 , ветви которой направлены вниз,
, ветви которой направлены вниз, 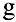 — гравитационная постоянная.
— гравитационная постоянная.
Тогда 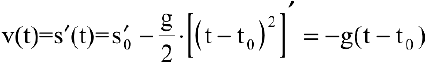 — скорость камня;
— скорость камня;
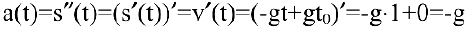 — его ускорение, что согласуется с известным физическим законом: всякое брошенное тело испытывает постоянное ускорение свободного падения.
— его ускорение, что согласуется с известным физическим законом: всякое брошенное тело испытывает постоянное ускорение свободного падения.
Производная неявной функции
Выше было рассмотрено дифференцирование явных функций, заданных формулой 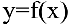 , правая часть которых не содержала зависимой переменной. Если же функция
, правая часть которых не содержала зависимой переменной. Если же функция 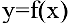 задана уравнением
задана уравнением 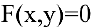 не разрешенным относительно зависимой переменной, то говорят, что функция у задана неявно.
не разрешенным относительно зависимой переменной, то говорят, что функция у задана неявно.
Внимание! Не всякое уравнение 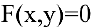 определяет неявную функцию. Например, уравнение
определяет неявную функцию. Например, уравнение 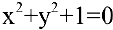 в действительной области не определяет никакой функции. Иногда одно уравнение такого вида может определять несколько функций. Например, уравнение
в действительной области не определяет никакой функции. Иногда одно уравнение такого вида может определять несколько функций. Например, уравнение 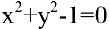 определяет две функции:
определяет две функции: 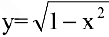 и
и 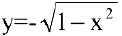 .
.
Часто разрешить уравнение 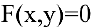 относительно переменной затруднительно. В таком случае функцию приходится изучать, пользуясь непосредственно уравнением, определяющим ее. Рассмотрим дифференцирование неявной функции, заданной уравнением
относительно переменной затруднительно. В таком случае функцию приходится изучать, пользуясь непосредственно уравнением, определяющим ее. Рассмотрим дифференцирование неявной функции, заданной уравнением 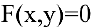 .
.
Для нахождения производной функции 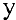 , заданной неявно, нужно продифференцировать обе части уравнения, рассматривая у как функцию от
, заданной неявно, нужно продифференцировать обе части уравнения, рассматривая у как функцию от 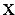 . Затем из полученного уравнения найти производную
. Затем из полученного уравнения найти производную 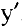 .
.
Пример №21
Покажите, что функция 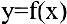 , заданная неявно выражением
, заданная неявно выражением 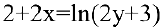 , удовлетворяет уравнению
, удовлетворяет уравнению 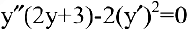 .
.
Решение:
Найдем первую производную данной функции. Для этого продифференцируем обе части уравнения 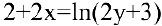 , используя формулы и правила дифференцирования:
, используя формулы и правила дифференцирования:
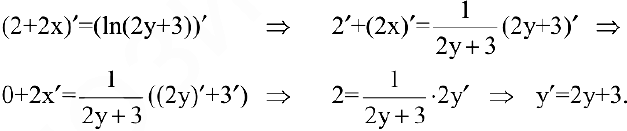
Найдем вторую производную:
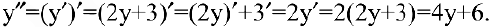
Подставим найденные выражения в дифференциальное уравнение:
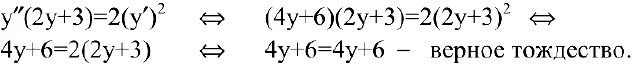
Правило Лопиталя
С помощью производной можно находить многие пределы. Следующее утверждение позволит свести предел отношения двух функций с случае неопределенностей вида 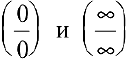 к пределу отношения производных, который очень часто вычисляется проще.
к пределу отношения производных, который очень часто вычисляется проще.
Правило Лопиталя. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если этот предел существует:
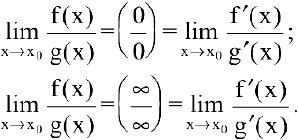
Внимание! В правой части формул берется отношение производных, а не производная отношения.
Пример №22
Вычислить предел 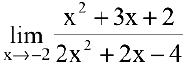
Решение:
Имеем неопределенность вида 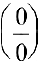 . Т.к. числитель и знаменатель дроби непрерывны и дифференцируемы, то можно применить правило Лопиталя:
. Т.к. числитель и знаменатель дроби непрерывны и дифференцируемы, то можно применить правило Лопиталя:
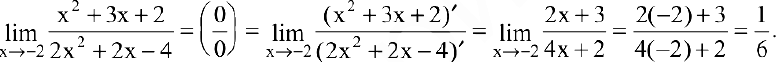
Замечание Правило Лопиталя можно применять повторно, если вновь приходим к соотношению неопределенностей вида 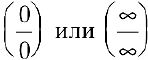 .
.
Пример №23
Вычислить предел 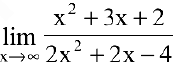
Решение:
Числитель и знаменатель дроби непрерывны, дифференцируемы и стремятся к бесконечности. Следовательно, можно применить правило Лопиталя (в данном примере мы воспользовались им дважды):
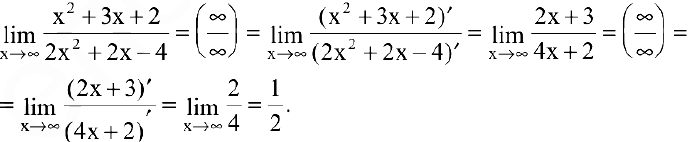
Замечание. Другие неопределенности раскрываются по правилу Лопиталя, если их предварительно свести к основному виду 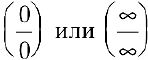 с помощью тождественных преобразований.
с помощью тождественных преобразований.
Пример №24
Найти 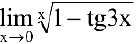 .
.
Решение:
Преобразуя выражение и используя непрерывность показательной функции, получим:
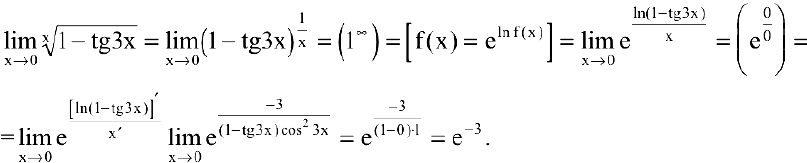
Оптимизация
В этом параграфе оптимизацию будем понимать как процесс нахождения экстремума (максимума или минимума) экономических функций, т.е. выбор наилучшего варианта из множества возможных. Говорят, что в точке 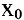 функция
функция 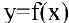 имеет (локальный) максимум, если существует такая окрестность точки
имеет (локальный) максимум, если существует такая окрестность точки 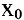 , что для всех
, что для всех 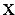 из этой окрестности выполнено условие
из этой окрестности выполнено условие 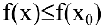 . Аналогично, функция
. Аналогично, функция 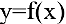 в точке
в точке 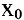 имеет (локальный) минимум, если существует такая окрестность точки
имеет (локальный) минимум, если существует такая окрестность точки 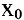 , что для всех х из этой окрестности выполнено условие
, что для всех х из этой окрестности выполнено условие 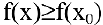 . Точки (локальных) максимума и минимума называются точками (локального) экстремума, а значение функции в них — (локальными) экстремумами функции.
. Точки (локальных) максимума и минимума называются точками (локального) экстремума, а значение функции в них — (локальными) экстремумами функции.
Внимание! Не следует путать понятие локального экстремума функции с ее наибольшим или наименьшим значением (так называемым глобальным максимумом или минимумом). На одном промежутке функция может иметь несколько экстремумов, причем минимум может оказаться больше максимума подобно тому, как впадина в горах может иметь большую отметку над уровнем моря, чем невысокая вершина. А наибольшее и наименьшее значение непрерывной на отрезке функции может достигаться как в точках экстремума, так и на концах отрезка.
Геометрически в точке экстремума касательная к графику функции либо горизонтальна, либо не существует.
Следовательно, непрерывная функция может иметь экстремум лишь в тех точках, где производная функции равна пулю или не существует (необходимое условие экстремума). Точки, в которых выполнено необходимое условие экстремума, называются критическими. (Иногда точки, в которых производная обращается в нуль, называют стационарными.)
Замечание. Критическая точка не обязательно является точкой экстремума. Это лишь точка возможного экстремума функции.
Достаточное условие экстремума. Если в критической точке вторая производная положительна, то это точка минимума, а если отрицательна — точка максимума.
Для запоминания этой теоремы предлагаем мнемоническое правило: если плюс — котелок наполняется, если минус — опустошается.
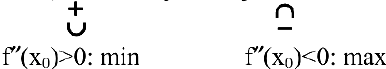
Пример №25
Пусть в краткосрочном плане производственная функция зависит только от численности персонала и имеет вид
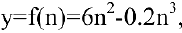
где у — выпуск продукции, а n — число работающих. Определить численность персонала, при которой выпуск у достигает максимального значения.
Решение:
Выпуск продукции 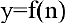 — функция натурального аргумента. Для решения задачи рассмотрим обобщенную функцию действительного аргумента
— функция натурального аргумента. Для решения задачи рассмотрим обобщенную функцию действительного аргумента 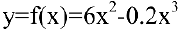 . Новая функция везде непрерывна и дифференцируема. Найдем стационарные точки, для чего вычислим производную и приравняем ее к нулю:
. Новая функция везде непрерывна и дифференцируема. Найдем стационарные точки, для чего вычислим производную и приравняем ее к нулю:
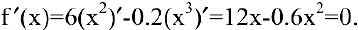
Решая квадратное уравнение, легко находим 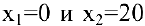 . Вычисляем вторую производную:
. Вычисляем вторую производную:
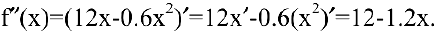
При 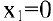 имеем
имеем
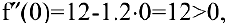
следовательно, в данной точке имеется минимум. Это естественно, т.к. нет выпуска продукции, если нет рабочих. Для второй точки
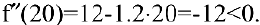
Поэтому в точке 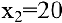 максимум. Соответствующий выпуск продукции
максимум. Соответствующий выпуск продукции
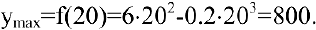
Исследование функции на монотонность
С помощью производной можно найти промежутки возрастания и убывания функции. Функция 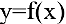 называется возрастающей (убывающей) на промежутке X, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции:
называется возрастающей (убывающей) на промежутке X, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции:
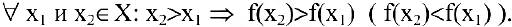
Возрастающие и убывающие функции называются монотонными.
Достаточное условие монотонности. Если производная дифференцируемой функции положительна (отрицательна) внутри некоторого промежутка X, то она возрастает (убывает) на этом промежутке:
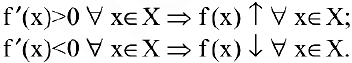
Таким образом, если при переходе через критическую точку производная дифференцируемой функции меняет знак с плюса на минус, то это точка (локального) максимума, а если с минуса на плюс — точка (локального) минимума (достаточное условие экстремума):
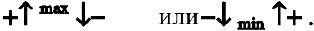
Если изменение знака производной не происходит, то экстремума нет.
Пример №26
Исследовать функцию 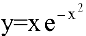 па монотонность.
па монотонность.
Решение:
Область определения функции 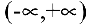 . С помощью первой производной найдем точки возможного экстремума:
. С помощью первой производной найдем точки возможного экстремума:
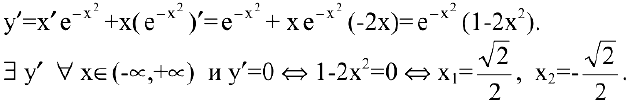
Эти точки разбивают область определения функции на интервалы монотонности. Результаты исследования удобно представить в таблице.

Итак, функция убывает на интервалах 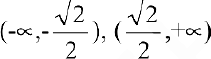 и возрастает на интервале
и возрастает на интервале 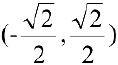 ; в точке
; в точке 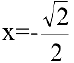 — имеем минимум:
— имеем минимум: 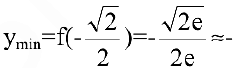
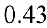
а 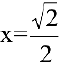 точка максимума:
точка максимума: 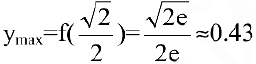
Выпуклость и вогнутость графика функции. Точки перегиба
График дифференцируемой функции 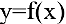 называется выпуклым (выпуклым вверх) в точке
называется выпуклым (выпуклым вверх) в точке 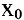 , если он расположен ниже касательной в некоторой окрестности этой точки. Аналогично, график дифференцируемой функции
, если он расположен ниже касательной в некоторой окрестности этой точки. Аналогично, график дифференцируемой функции 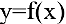 называется вогнутым (выпуклым вниз) в точке х0, если он расположен выше касательной в некоторой окрестности этой точки. Однако могут существовать точки, слева от которых в некоторой в достаточно малой окрестности график лежит по одну сторону от касательной, а справа — по другую. Точки графика, в которых выпуклость меняется на вогнутость или наоборот, называются точками перегиба.
называется вогнутым (выпуклым вниз) в точке х0, если он расположен выше касательной в некоторой окрестности этой точки. Однако могут существовать точки, слева от которых в некоторой в достаточно малой окрестности график лежит по одну сторону от касательной, а справа — по другую. Точки графика, в которых выпуклость меняется на вогнутость или наоборот, называются точками перегиба.
Достаточное условие направления выпуклости. Если вторая производная дважды дифференцируемой функции отрицательна [положительна) внутри некоторого промежутка, то функция выпукла (вогнута) на этом промежутке:
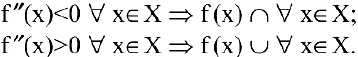
Следовательно, если вторая производная дважды дифференцируемой функции при переходе через некоторую точку меняет знак, то это точка перегиба (достаточное условие перегиба):
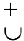 точка перегиба
точка перегиба 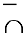 или
или 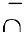 точка перегиба
точка перегиба 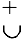 .
.
Отсюда вытекает необходимое условие перегиба: вторая производная дважды дифференцируемой функции в точке перегиба равна нулю или не существует.
Замечание. Если критическая точка дифференцируемой функции не является точкой экстремума, то это точка перегиба.
Пример №27
Исследовать функцию 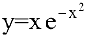 на выпуклость и точки перегиба.
на выпуклость и точки перегиба.
Решение:
Область определения функции 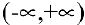 . С помощью второй производной найдем точки возможного перегиба:
. С помощью второй производной найдем точки возможного перегиба:
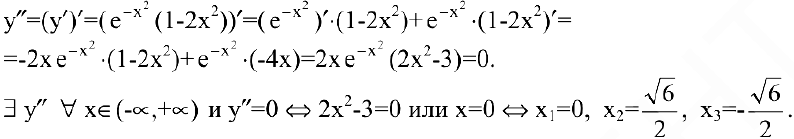
Эти точки разбивают область определения функции на интервалы, в которых сохраняется направление выпуклости или вогнутости. Результаты удобно представить в таблице.

Кривая, изображающая график функции, выпукла на интервалах 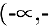
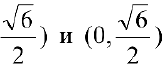 и вогнута на интервалах
и вогнута на интервалах 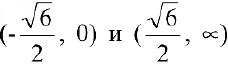 . В точках
. В точках 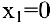 ,
, 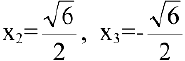 имеем перегиб:
имеем перегиб:
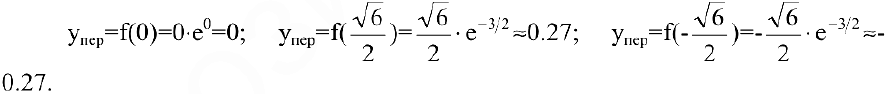
Асимптоты графика функции
При исследовании поведения функции на бесконечности или вблизи точек разрыва часто оказывается, что расстояние между точками графика функции и точками некоторой прямой стремится к нулю при неограниченном удалении точек графика от начала координат. Прямая, к которой стремится кривая в бесконечно удаленной точке, называется асимптотой графика. Различают вертикальные и наклонные асимптоты. Прямая 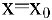 называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции 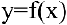 , если хотя бы один из односторонних пределов в точке
, если хотя бы один из односторонних пределов в точке 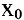 равен бесконечности:
равен бесконечности: 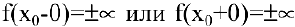 . Такие асимптоты существуют только в точках разрыва второго рода.
. Такие асимптоты существуют только в точках разрыва второго рода.
Внимание! Непрерывные на множестве действительных чисел функции вертикальных асимптот на имеют.
Для того чтобы график функции 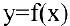 имел наклонную асимптоту
имел наклонную асимптоту 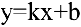 , необходимо и достаточно, чтобы существовали конечные пределы
, необходимо и достаточно, чтобы существовали конечные пределы
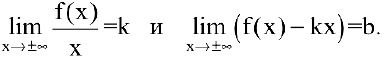
Частным случаем наклонной асимптоты 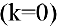 является горизонтальная асимптота.
является горизонтальная асимптота.
Пример №28
Найти асимптоты графика функции 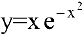 .
.
Решение:
Функция 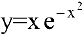 непрерывна в области определения
непрерывна в области определения 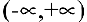 как элементарная. Следовательно, вертикальных асимптот пет. Найдем наклонные асимптоты
как элементарная. Следовательно, вертикальных асимптот пет. Найдем наклонные асимптоты 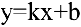 :
:
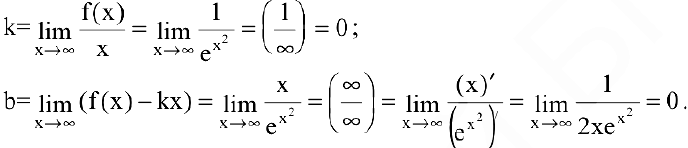
Получаем горизонтальную асимптоту 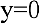 .
.
Кстати теория из учебников по математическому анализу тут.
Общее исследование функции и построение графика
С помощью производной функции можно провести ее полное исследование и построить график этой функции. При этом рекомендуется использовать следующую схему.
- Найти область определения функции
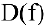
- Исследовать функцию на четность
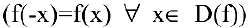 ; нечетность
; нечетность 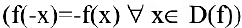 ; периодичность
; периодичность 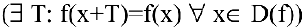 .
. - Исследовать функцию на непрерывность, найти точки разрыва.
- Найти асимптоты графика функции.
- Исследовать функцию на монотонность, найти точки экстремума.
- Найти интервалы выпуклости и вогнутости, точки перегиба функции.
- Используя результаты проведенного исследования, построить график функции (можно вычислить координаты точек пересечения с осями координат).
Пример №29
Провести полное исследование функции 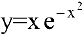 и построить ее график.
и построить ее график.
Решение:
- Область определения функции — вся числовая прямая:
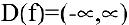 .
. - Функция непериодическая. Она нечетная, т.к. область определения симметрична относительно начала координат и
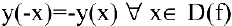 :
:
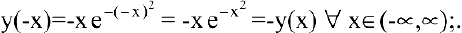
Следовательно, график функции симметричен относительно начала координат и достаточно исследовать функцию для 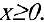 .
.
3. Функция непрерывна в области определения как композиция основных элементарных функций. Поскольку 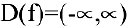 , точек разрыва нет.
, точек разрыва нет.
4. Строим график функции, используя результаты исследования.