Случай неабсолютно сходящихся рядов

Оглавление:

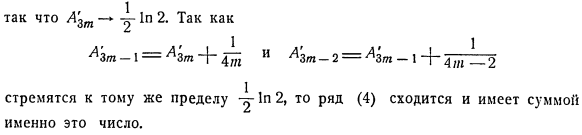
Случай неабсолютно сходящихся рядов

Случай неабсолютно сходящихся рядов. Теперь перейдем к рассмотрению неабсолютных сходящихся рядов и установим, что они не обладают транзитивными свойствами. 1 сделать предварительное заявление. Предположим, что ряд (а) сходится, но он не является абсолютным. Из сходимости, ПшЛЛ = 0 [N ° 236, 5°].Звание есть 2 БК ©, 2 ст. л. (о、 &= 1 т = я Упоминалось в предыдущем номере, но видимо、 Bkbk = 0 и ншст = 0, (2） к• * ОО, Т «ОО Но в данном случае они diverge. In факт, если первые n членов ряда (A) имеют k положительных и m отрицательных、 К = БК-Ст, К = Ьк \ С. 2-й из этих уравнений показывает, что оба ряда (B) и © не могут сходиться одновременно. В противном случае ряд (A) будет сходиться против предположения. Здесь мы докажем следующие интересные теоремы: Теорема Римана.

И с самого начала мы видим, что если одна из этих линий сходится, а другая не сходится, то линия (а) расходится, но это также противоречит предположениям. Людмила Фирмаль

Если ряд (A) сходится не абсолютно, если заранее получено число k, равное конечному или±Oo, то члены этого ряда можно переставить так, чтобы сумма преобразованного ряда была точно b. Доказательство. Рассмотрим случай конечного E. in термины n°236, 1°и все остатки в строках (B) и © также расходятся, поэтому вы можете накопить много терминов в каждой из этих строк, начиная с любого location. So что сумма превышает любое число. Используйте это, чтобы изменить условия ряда следующим образом (A). Во-первых, мы получаем столько положительных членов ряда, в том порядке, в котором они расположены, что сумма превышает число V. + ^ 2 +•• + Вслед за ними выпишите отрицательные термины(в том порядке, в котором они расположены в этой строке), чтобы общая сумма была меньше I. ^ 1 + ^ 2• * * » б ^-с -СГ-**•После этого положительные условия снова помещаются из числа оставшихся условий.

Затем выберите так много отрицательных членов из числа оставшихся членов. +. •* + БК% -СХ —…ТТ ^ + БК ^ +1 +•••+ + БС-СТ%+ 1-•••ст с ^ И так далее. Процесс, о котором мы думаем, продолжается бесконечно. Очевидно, что каждый член Серии (А), кроме того, со своей собственной подписью, встречается в определенном месте. Тогда серия из(2) (П \ +•вк1)-(С1 + * * + СС1)+ —Есть такая сумма. Аннотация по N°245 остается этот путь даже после того, как скобка раскрывается. в случае b =\ oo множество положительных чисел может быть подчинено таким требованиям, что сумма равна 1, 2, 3 и т. д. последовательно, и из отрицательных членов, только 1 помещается после каждой группы положительных. Таким образом, по-видимому, образуется ряд с суммой | oo.

Каждый раз вы выписываете термины b или c и не принимаете их больше, чем необходимо для реализации необходимых неравенств, отклонение от числа I в ту или иную сторону не превышает абсолютного значения последнего записанного члена. Людмила Фирмаль

Аналогично можно получить серию в сумме -°°. Установленные результаты подчеркивают тот факт, что абсолютная конвергенция осуществляется только путем взаимного аннулирования положительных и отрицательных членов», говорит он, так что, хотя абсолютная конвергенция основана на скорости сокращения этих членов, она в значительной степени зависит от следующего порядка и не зависит от их порядка. (3） (4 )） Мы утверждаем, что сумма рядов от такого хода уменьшится вдвое. Фактически, если вы представляете частичные суммы этих рядов с помощью An и A’N соответственно、 т т т т Lzt = 21(^ =Л4Г= 2-4©) = 21 {w = 2-u)= кра1 к = 1 *) Здесь важно, чтобы эта сумма была ненулевой Так что это ’ rt + y1n2.С ^ 3m-1 = / Th + 4 ^и^ 3m-2 = ^ 3m-1 + 4m _2 Существует тенденция к тому же ограничению y1n2, ряд (4) сходится, и именно это число является суммой.

Сочетательное свойство.	Умножение рядов.
Переместительное свойство абсолютно сходящихся рядов.	Бесконечные произведения Основные понятия.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.