Скалярное волновое уравнение

Скалярное волновое уравнение

Скалярное волновое уравнение. Для дальнейшего изучения характеристик и решения векторного волнового уравнения гидравлического удара (7.19) рассмотрим основные особенности скалярного волнового уравнения Где G (x, I) неизвестная функция. C-константа с размерностью скорости. Очевидно, когда вы устанавливаете связь между dx и (H Левую часть уравнения (7.20)можно представить в виде полной производной функции Γ.

В одномерном случае уравнение называется также уравнением колебания струны или уравнением продольных колебаний стержня. Людмила Фирмаль

• В результате физический план по линиям (x, I) o>согласно уравнению (7.22), функция Γ(x, 1) сохраняет постоянное значение. Рассмотрим задачу Коши по формуле (7.20) и примем начальное условие 1-0(рис. 7.4） Решение уравнения (7.20), то есть значение функции Γ в любой точке (x, I) физического плана, имеет вид Γ (x, I)=Γ(x0, 0) = Γ0(x0). (7.24).

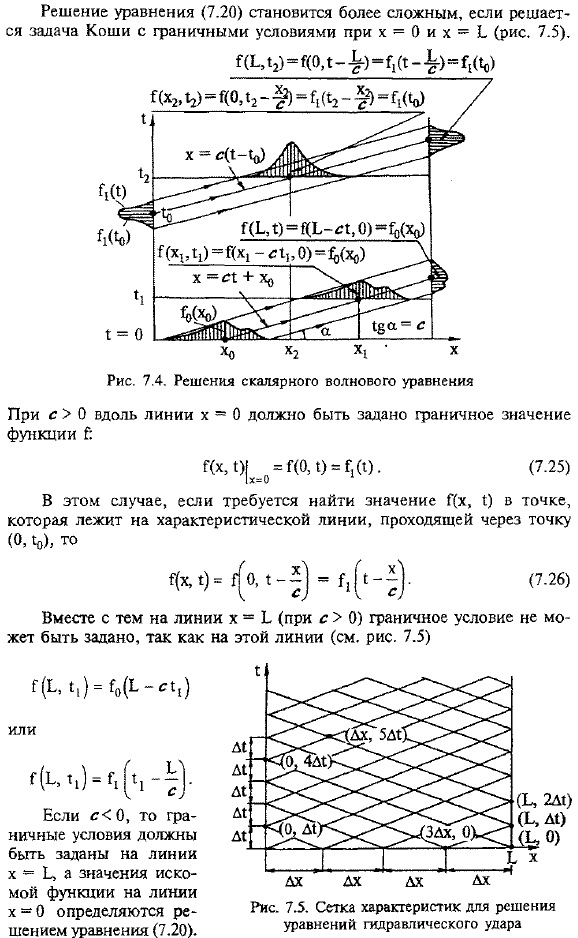
• Линия x-cx + x0 называется характеристикой характеристической линии или уравнением(7.20). если c равно 0, то угол a тупой. Сто пятьдесят два решение задачи Коши с граничными условиями x = 0 и x = I усложняет решение уравнения (7.20) (рис.7.5). Для c> 0 вдоль линии x = 0 необходимо указать граничное значение функции Gamma.

В многомерном случае также решение задачи Коши может быть разложено в бегущие волны, однако уже не в сумму, а в интеграл, поскольку направлений становится бесконечно много. Это делается элементарно при помощи преобразования Фурье. Людмила Фирмаль

• В этом случае, когда необходимо найти значение Γ (x, 1) в точке, которая находится на характеристической линии через точку (0.10、 О-26） В то же время нельзя указать граничное условие в строке x = E(если c> 0). в этой строке (см. Рисунок 7.5） Ч) М31 Или для c 0 граничное условие должно быть задано в строке x-b, а значение искомой функции для строки x = 0 определяется решением уравнения(7.20).

Смотрите также:

Примеры решения задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Общее описание гидравлического удара.
2. Основные уравнения гидравлического удара.
3. Векторные волновые уравнения.
4. Волновая скорость.