Системы линейных уравнений m*n
Система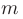 
линейных уравнений, содержащая 
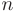неизвестных величин имеет вид
Используя правила действий над матрицами, вышеуказанную систему уравнений можно представить в виде
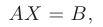
где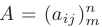 
— прямоугольная матрица коэффициентов системы размера 
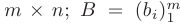— матрица-столбец свободных членов размера 
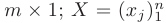— матрица-столбец неизвестных величин размера 
.
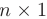Расширенной матрицей системы уравнений называется матрица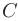 
, полученная в результате добавления к матрице коэффициентов 
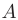матрицы свободных членов 
:
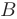С расширенной матрицей системы связано свойство совместности системы линейных уравнений 
. В частности, в теореме Кронекера-Капслли доказывается, что для совместности системы линейных уравнений необходимо и достаточно, чтобы ранг матрицы коэффициентов системы был равен ранг ее расширенной матрицы:
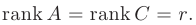
Заметим, что базисными неизвестными совместной системы линейных уравнений называют любые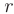 
неизвестных, коэффициенты при которых образуют отличный от нуля определитель — базисный минор. Тогда остальные 
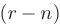неизвестных называют свободными.
Две системы линейных уравнений называются равносильными, если множества их решений совпадают.
Одним из наиболее эффективных методов решения систем линейных уравнений является метод Гаусса, построенный на применении элементарных преобразований (см. раздел 1.6). Если в результате этих преобразований появляется уравнение вида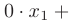 
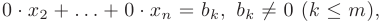то исходная система несовместна, т. к. нарушается условие теоремы Кронекера-Капелли. В противном случае исходная система уравнений приводится к трапециевидной форме:
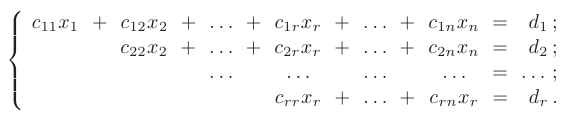
В частности, если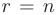 
, то система приведена к треугольному виду и имеет единственное решение. Причем, из последнего уравнения можно найти значение 
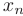, из предпоследнего — 
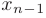и т.д.
Если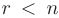 
, то переменные 
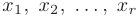в системе будут базисными. а остальные 
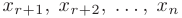— свободными. Выразим базисные переменные через свободные:
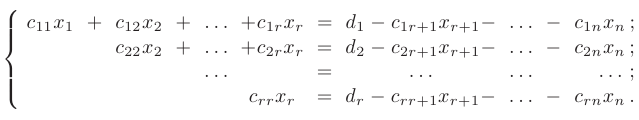
Выразим в последнем уравнении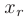 
, поделив обе его части на 
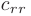и подставим в предыдущее уравнение. Выразим 
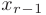из предпоследнего уравнения и подставим в третье снизу уравнение и т.д. Таким образом, определим значения переменных 
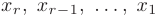через неизвестные 
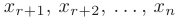. Т.е. получим общее решение, описывающие множество допустимых решений исходной системы :
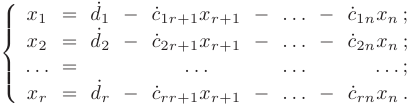
Если свободные переменные принять равными нулю, то получим допустимое базисное решение.
Таким образом, метод Гаусса позволяет одновременно провести исследование системы линейных уравнений на совместность и, если она совместна, — решить ее.
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Системы линейных уравнений n*n в математике |
| Ранг матрицы в математике |
| Собственные значения и собственные векторы матрицы в математике |
| Квадратичные формы в матричной записи в математике |
