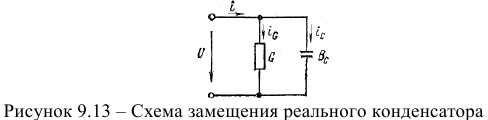
Схема замещения конденсатора с параллельным соединением элементов. Векторная диаграмма токов в цепи с конденсатором
В реальном конденсаторе наряду с изменением энергии электрического поля (это характеризует реактивная мощность 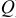 ) из-за несовершенства диэлектрика идет необратимый процесс преобразования электрической энергии в тепло, скорость которого выражается активной мощностью
) из-за несовершенства диэлектрика идет необратимый процесс преобразования электрической энергии в тепло, скорость которого выражается активной мощностью 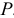 . Поэтому в схеме замещения реальный конденсатор должен быть представлен активным и реактивным элементами.
. Поэтому в схеме замещения реальный конденсатор должен быть представлен активным и реактивным элементами.
Реальный конденсатор (с потерями) можно представить эквивалентной схемой параллельного соединения активной 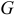 и емкостной
и емкостной 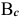 проводимостей (рис. 9.13), причем активная проводимость определяется мощностью потерь в конденсаторе
проводимостей (рис. 9.13), причем активная проводимость определяется мощностью потерь в конденсаторе 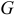
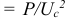 , а емкость — конструкцией конденсатора.
, а емкость — конструкцией конденсатора.
Предположим, что проводимости 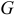 и
и 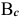 для такой цепи известны, а напряжение имеет уравнение
для такой цепи известны, а напряжение имеет уравнение 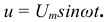
Требуется определить токи в цепи и мощность.
Исследование цепи с активным сопротивлением и цепи с емкостью показало, что при синусоидальном напряжении токи в них так же синусоидальны. При параллельном соединении ветвей 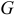 и
и 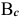 , согласно первому закону Кирхгофа, общий ток
, согласно первому закону Кирхгофа, общий ток 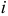 равен сумме токов в ветвях с активной и емкостной проводимостями:
равен сумме токов в ветвях с активной и емкостной проводимостями: 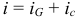 .
.
Для определения действующей величины общего тока 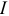 методом векторного сложения построим векторную диаграмму согласно уравнению:
методом векторного сложения построим векторную диаграмму согласно уравнению: 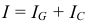 Действующие величины составляющих тока:
Действующие величины составляющих тока: 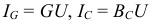 .
.
Первым на векторной диаграмме изображается вектор напряжения 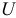 (рис. 9.14 а), его направление совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза напряжения
(рис. 9.14 а), его направление совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза напряжения 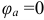 ).
).
Вектор 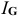 совпадает по направлению с вектором
совпадает по направлению с вектором 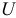 , а вектор
, а вектор 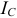 направлен перпендикулярно вектору
направлен перпендикулярно вектору 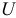 с положительным углом. Из векторной диаграммы видно, что вектор общего напряжения отстает от вектора общего тока на угол
с положительным углом. Из векторной диаграммы видно, что вектор общего напряжения отстает от вектора общего тока на угол 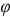 , величина которого больше нуля, но меньше 90°. Вектор
, величина которого больше нуля, но меньше 90°. Вектор 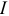 является гипотенузой прямоугольного треугольника, катеты которого — составляющие его векторы
является гипотенузой прямоугольного треугольника, катеты которого — составляющие его векторы 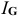 и
и 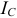 :
:

При напряжении 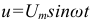 в соответствии с векторной диаграммой уравнение тока
в соответствии с векторной диаграммой уравнение тока 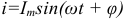 .
.
Стороны треугольников токов, выраженные в единицах тока, разделим на напряжение 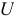 . Получим подобный треугольник проводимостей (рис. 9.14 6), катетами которого являются активная
. Получим подобный треугольник проводимостей (рис. 9.14 6), катетами которого являются активная 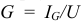 и емкостная
и емкостная 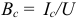 проводимости, а гипотенузой — полная проводимость цепи
проводимости, а гипотенузой — полная проводимость цепи 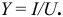
Из треугольника проводимостей: 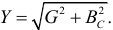
Эта страница взята со страницы лекций по предмету теоретические основы электротехники (ТОЭ):
Предмет теоретические основы электротехники
Возможно эти страницы вам будут полезны:

