Оглавление:
Схема исследования функции и построения ее графика
Рассмотрим примерный план, по которому целесообразно исследовать поведение функции и строить ее график:
- Найти область определения функции.
- Проверить выполнение свойств четности или нечетности, периодичности.
- Указать промежутки непрерывности, точки разрыва и их тип, проверить наличие асимптот.
- Найти промежутки монотонности и точки экстремума.
- Найти промежутки выпуклости и вогнутости, точки перегиба.
- Найти точки пересечения графика функции с осями координат.
- Построить график функции.
Замечание 9.5. Если исследуемая функция 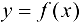 четная, то достаточно исследовать функцию и построить ее график при положительных значениях аргумента, принадлежащих области определения функции. При отрицательных значениях аргумента график функции строится на том основании, что график четной функции симметричен относительно оси ординат.
четная, то достаточно исследовать функцию и построить ее график при положительных значениях аргумента, принадлежащих области определения функции. При отрицательных значениях аргумента график функции строится на том основании, что график четной функции симметричен относительно оси ординат.
Замечание 9.6. Если исследуемая функция 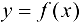 нечетная, то достаточно исследовать функцию и построить ее график при положительных значениях аргумента, принадлежащих области определения функции. При отрицательных значениях аргумента график функции строится на том основании, что график нечетной функции симметричен относительно начала координат.
нечетная, то достаточно исследовать функцию и построить ее график при положительных значениях аргумента, принадлежащих области определения функции. При отрицательных значениях аргумента график функции строится на том основании, что график нечетной функции симметричен относительно начала координат.
Пример 9.7.
Исследовать функцию 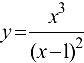 и построить ее график.
и построить ее график.
Решение:
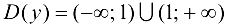
- Так как область определения функции несимметрична относительно начала координат, то эта функция общего вида, т. е. функция ни четная, ни нечетная, непериодическая.
- Функция непрерывна на области определения как элементарная. Точкой разрыва является
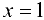 . Так как
. Так как
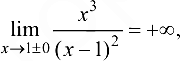
то 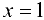 — точка разрыва второго рода. Можно также сделать заключение, что прямая
— точка разрыва второго рода. Можно также сделать заключение, что прямая 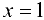 будет являться вертикальной асимптотой графика функции.
будет являться вертикальной асимптотой графика функции.
Проверим наличие горизонтальных асимптот. Так как
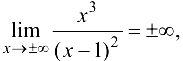
то данная функция не имеет горизонтальных асимптот.
Проверим наличие наклонных асимптот. Так как
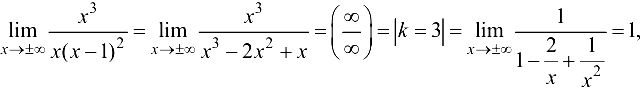
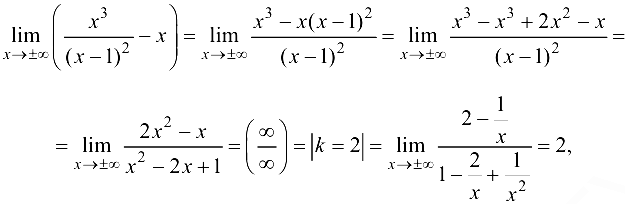
то график функции имеет наклонную асимптоту с угловым коэффициентом 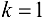 и свободным членом
и свободным членом 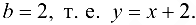 .
.
4. Определим промежутки возрастания и убывания функции, точки экстремума. Для этого найдем критические точки первого рода:
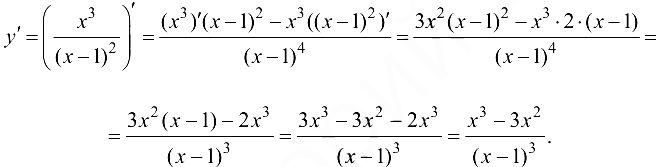
Решим уравнение 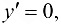 т. е.
т. е. 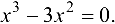 . Получаем
. Получаем 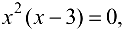 , откуда
, откуда 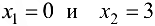 — критические точки первого рода. Изменение знака первой производной покажем на числовой оси (рис. 9.4).
— критические точки первого рода. Изменение знака первой производной покажем на числовой оси (рис. 9.4).
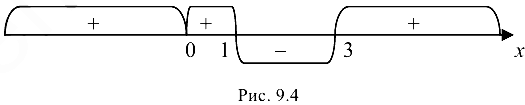
Так как 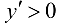 при
при 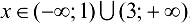 , то функция возрастает на указанных промежутках: так как
, то функция возрастает на указанных промежутках: так как 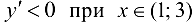 , то функция убывает на указанном промежутке. При переходе через точку
, то функция убывает на указанном промежутке. При переходе через точку 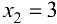 производная
производная 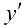 изменяет знак с «-» па «+», следовательно, в этой точке функция имеет минимум, причем
изменяет знак с «-» па «+», следовательно, в этой точке функция имеет минимум, причем 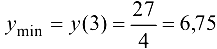 .
.
5. Определим промежутки выпуклости и вогнутости графика функции, точки перегиба. Для этого найдем критические точки второго рода:
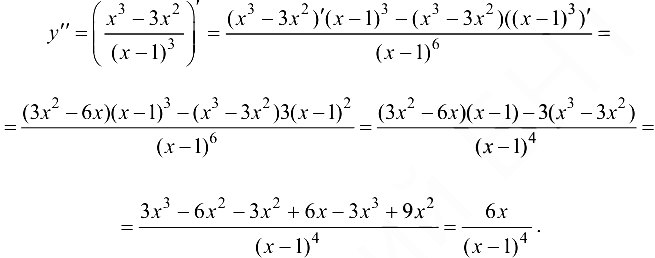
Решим уравнение 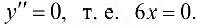 . Получаем единственное решение
. Получаем единственное решение 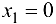 — критическая точка второго рода. Изменение знака второй производной покажем на числовой оси (рис. 9.5).
— критическая точка второго рода. Изменение знака второй производной покажем на числовой оси (рис. 9.5).

Так как 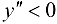 при
при 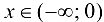 , то график функции будет выпуклым на данном промежутке; так как
, то график функции будет выпуклым на данном промежутке; так как 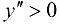 при
при 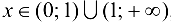 , то график функции будет вогнутым на указанных промежутках. При переходе через точку
, то график функции будет вогнутым на указанных промежутках. При переходе через точку 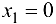 выпуклость графика функции сменяется вогнутостью, следовательно, это абсцисса точки перегиба, тогда ордината
выпуклость графика функции сменяется вогнутостью, следовательно, это абсцисса точки перегиба, тогда ордината 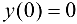 . Таким образом, (0;0) — точка перегиба графика функции.
. Таким образом, (0;0) — точка перегиба графика функции.
6. Найдем точки пересечения графика функции с осями координат.
Для точек оси 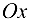 всегда
всегда 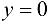 , т. е.
, т. е. 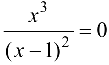 , откуда
, откуда 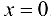 .
.
Для точек оси 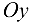 всегда
всегда 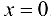 , т. е.
, т. е. 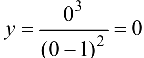 .
.
Таким образом, единственной точкой пересечения графика функции с осями координат является начало системы координат 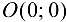 .
.
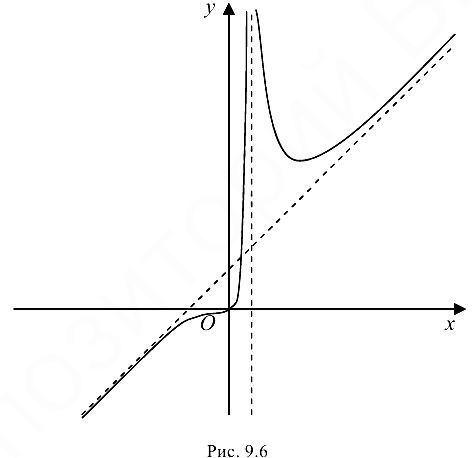
7. Построим график функции на рис. 9.6.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:

