Оглавление:
Во введении мы говорили, что теория вероятностей имеет дело с такими явлениями, при которых испытания можно повторять, по крайней мере теоретически, бесконечное число раз, и при этом появление или непоявление некоторого наблюдаемого события в каждом испытании не будет зависеть от исходов предыдущих испытаний. Сейчас мы рассмотрим более подробно эту схему, носящую в теории вероятностей название последовательности независимых одинаковых испытаний, или схемы Бернулли, основываясь на аксиоматическом определении вероятности и уже введенном нами понятии независимости событий.
Итак, опыт состоит в n-кратном повторении одинаковых испытаний, в каждом из которых может с вероятностью р наступить некоторое событие (будем говорить в этом случае, что произошел «успех») или с вероятностью 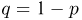 не наступить (произошла «неудача»). Результат каждого опыта можно записать в виде последовательности УНН…У, состоящей из n букв У и Н, причем буква У (или Н) на i-м месте означает, что в i-м испытании произошел успех (или неудача). Пространство элементарных исходов
не наступить (произошла «неудача»). Результат каждого опыта можно записать в виде последовательности УНН…У, состоящей из n букв У и Н, причем буква У (или Н) на i-м месте означает, что в i-м испытании произошел успех (или неудача). Пространство элементарных исходов 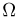 состоит из
состоит из 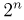 исходов, каждый из которых отождествляется с определенной последовательностью УНН…У (
исходов, каждый из которых отождествляется с определенной последовательностью УНН…У (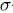 -алгебра событий
-алгебра событий 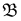 включает
включает 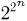 событий!). Заметим теперь, что в силу независимости испытаний мы обязаны сопоставить каждому элементарному исходу
событий!). Заметим теперь, что в силу независимости испытаний мы обязаны сопоставить каждому элементарному исходу 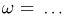 вероятность
вероятность 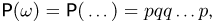 причем буква р (или q) в произведении повторяется столько раз, сколько раз произошел успех (или неудача). Типичным представителем схемы Бернулли является n-кратное подбрасывание несимметричной монеты, причем, например, «успех» означает выпадение «герба», а «неудача» — «цифры».
причем буква р (или q) в произведении повторяется столько раз, сколько раз произошел успех (или неудача). Типичным представителем схемы Бернулли является n-кратное подбрасывание несимметричной монеты, причем, например, «успех» означает выпадение «герба», а «неудача» — «цифры».
Формула Бернулли
Вычислим вероятность 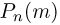 получить в n испытаниях ровно m успехов. Событие
получить в n испытаниях ровно m успехов. Событие 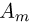 — в n испытаниях произошло ровно m успехов — состоит из тех элементарных исходов, в которых буква У появляется ровно m раз. Для того чтобы подсчитать число таких исходов, заметим, что оно совпадает с числом способов, которыми можно расставить m букв У на n местах. Поскольку порядок, в котором мы расставляем буквы, нас не интересует то мы имеем дело с со четаниями и число способов равно
— в n испытаниях произошло ровно m успехов — состоит из тех элементарных исходов, в которых буква У появляется ровно m раз. Для того чтобы подсчитать число таких исходов, заметим, что оно совпадает с числом способов, которыми можно расставить m букв У на n местах. Поскольку порядок, в котором мы расставляем буквы, нас не интересует то мы имеем дело с со четаниями и число способов равно 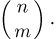 С другой стороны, каждый элементарный исход, в котором интересующая нас буква У встречается ровно m раз, как мы знаем, имеет вероятность
С другой стороны, каждый элементарный исход, в котором интересующая нас буква У встречается ровно m раз, как мы знаем, имеет вероятность 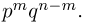 Окончательно получаем для вероятности
Окончательно получаем для вероятности 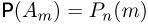 наступления m успехов в n независимых испытаниях формулу Бернулли:
наступления m успехов в n независимых испытаниях формулу Бернулли:
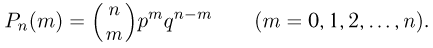
Данное выражение носит также название биномиального закона, поскольку 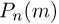 можно получить как коэффициент при
можно получить как коэффициент при 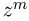 разложения по степеням z бинома
разложения по степеням z бинома 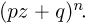 Заметим, что последнее выражение представляет собой производящую функцию (z-преобразование) для биномиального закона (см. параграф 3 гл. 8); аппарат производящих функций широко используется в теории вероятностей.
Заметим, что последнее выражение представляет собой производящую функцию (z-преобразование) для биномиального закона (см. параграф 3 гл. 8); аппарат производящих функций широко используется в теории вероятностей.
Пример:
В шаре радиусом R находится n молекул идеального газа. Вычислим вероятность того, что ровно т из них будут находиться на расстоянии, меньшем 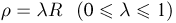 от центра этого шара. Поскольку каждая из п молекул может находиться в любой точке шара независимо от остальных, искомая вероятность определяется с помощью формулы Бернулли. При этом для вычисления вероятности р попадания одной молекулы в шар радиусом р (успех) можно воспользоваться схемой геометрической вероятности, т. е.
от центра этого шара. Поскольку каждая из п молекул может находиться в любой точке шара независимо от остальных, искомая вероятность определяется с помощью формулы Бернулли. При этом для вычисления вероятности р попадания одной молекулы в шар радиусом р (успех) можно воспользоваться схемой геометрической вероятности, т. е.
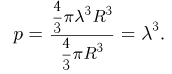
Тогда по формуле Бернулли окончательно получаем
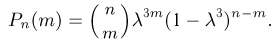
Пример:
Частица пролетает последовательно мимо 6 счетчиков. Каждый счетчик независимо от остальных отмечает ее пролет с вероятностью р = 0,8. Частица считается зарегистрированной (событие А), если она отмечена не менее чем двумя счетчиками. Найдем вероятность зарегистрировать частицу. В соответствии с аксиомой сложения искомую вероятность Р(A) можно представить в виде
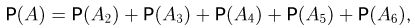
где 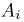 — событие, заключающееся в том, что частица отмечена ровно i счетчиками. Теперь для определения
— событие, заключающееся в том, что частица отмечена ровно i счетчиками. Теперь для определения 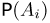 можно было бы воспользоваться формулой Бернулли, однако мы предварительно перейдем к дополнительному событию
можно было бы воспользоваться формулой Бернулли, однако мы предварительно перейдем к дополнительному событию 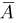 — частица либо не отмечена ни одним счетчиком, либо отмечена только одним. Тогда
— частица либо не отмечена ни одним счетчиком, либо отмечена только одним. Тогда
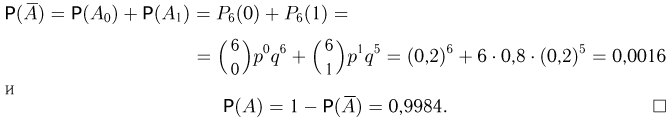
Формула Пуассона
Предположим, что мы хотим определить вероятность выпадения ровно 5100 «гербов» при 10000 бросаний монеты. Ясно, что при таком большом числе испытаний использование формулы Бернулли весьма затруднительно с точки зрения вычислений. Поэтому возникает естественное желание иметь простые, но достаточно точные приближенные формулы для вычисления 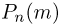 при больших п. Такие формулы существуют и определяются теоремой Пуассона, а также локальной и интегральной теоремами Муавра-Лапласа.
при больших п. Такие формулы существуют и определяются теоремой Пуассона, а также локальной и интегральной теоремами Муавра-Лапласа.
Начнем с наиболее простой из них — формулы Пуассона. Формула Пуассона применяется тогда, когда наряду с большим значением числа испытаний п мала вероятность успеха р. Рекомендации по применению предельных формул (в том числе и формулы Пуассона) мы дадим ниже. Сейчас же сформулируем теорему Пуассона. Строго математически теорема Пуассона опирается на довольно сложное понятие схемы серий, поэтому ниже мы приведем «инженерную» интерпретацию этой теоремы.
Теорема Пуассона:
Пусть число испытаний п в схеме Бернулли велико, а вероятность успеха р в одном испытании мала, причем мало также произведение 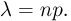 Тогда
Тогда 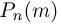 определяется по приближенной формуле (формула Пуассона)
определяется по приближенной формуле (формула Пуассона)
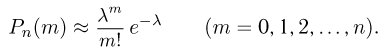
Доказательство:
Запишем формулу Бернулли
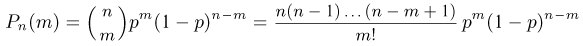
или, с учетом обозначения 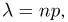
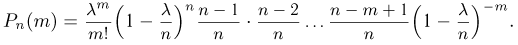
Как известно, 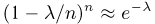 при больших п. Кроме того, если п велико, то
при больших п. Кроме того, если п велико, то 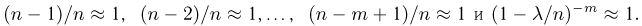
Поэтому
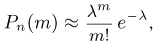
что и требовалось доказать.
Совокупность вероятностей 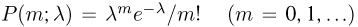 называется распределением Пуассона.
называется распределением Пуассона.
Значения функции 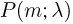 для некоторых
для некоторых 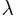 приведены в табл. 1 приложения.
приведены в табл. 1 приложения.
Отметим, что формула Пуассона справедлива также по отношению к числу неудач, но только в том случае, когда мало 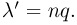
Формулы Муавра-Лапласа
Если в схеме Бернулли наряду с числом испытаний п велики также значения 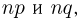 то следует применять формулы Муавра-Лапласа — локальную или интегральную. При этом локальную формулу Муавра-Лапласа, как следует из самого названия, необходимо применять в том случае, когда нас интересует вероятность получить ровно m успехов в п испытаниях, а интегральную — если определяется вероятность получить число успехов, заключенное в пределах от
то следует применять формулы Муавра-Лапласа — локальную или интегральную. При этом локальную формулу Муавра-Лапласа, как следует из самого названия, необходимо применять в том случае, когда нас интересует вероятность получить ровно m успехов в п испытаниях, а интегральную — если определяется вероятность получить число успехов, заключенное в пределах от 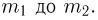
Так же, как и теорема Пуассона, локальная и интегральная теоремы Муавра-Лапласа приводятся в «инженерной» трактовке.
Локальная теорема Муавра-Лапласа:
Если в схеме Бернулли число испытаний п велико, то для всех m справедлива приближенная формула (локальная формула Муавра-Лапласа)
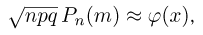
где 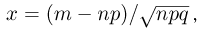 а
а
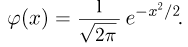
Одно из первых доказательств теоремы было основано на известной из курса математического анализа формуле Стирлинга
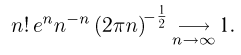
Не вдаваясь в математические подробности доказательства, изложим основную его суть. Считая, что n и  достаточно велики, и подставляя в формулу Бернулли вместо
достаточно велики, и подставляя в формулу Бернулли вместо  их приближенные значения, вычисленные по формуле Стирлинга, получаем
их приближенные значения, вычисленные по формуле Стирлинга, получаем
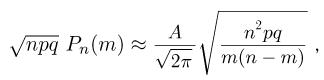
где
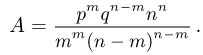
Положим 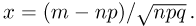 Тогда
Тогда 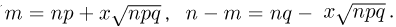 Логарифмируя теперь А, имеем
Логарифмируя теперь А, имеем
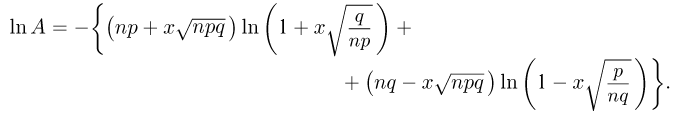
Поскольку 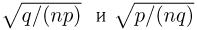 малы при больших п, разложим логарифмы в ряд Маклорена по степеням x до второго члена. Тогда
малы при больших п, разложим логарифмы в ряд Маклорена по степеням x до второго члена. Тогда
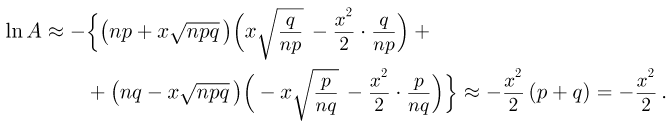
Следовательно,
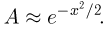
Наконец, учитывая, что 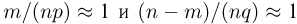 при фиксированном х и больших п, получаем
при фиксированном х и больших п, получаем
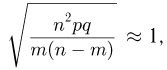
откуда и вытекает утверждение теоремы.
Значения функции 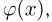 которую называют плотностью стандартного нормального, или гауссова, распределения, для некоторых х приведены в табл.2 приложения. Поскольку функция
которую называют плотностью стандартного нормального, или гауссова, распределения, для некоторых х приведены в табл.2 приложения. Поскольку функция 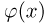 является четной, то при определении
является четной, то при определении 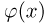 для отрицательных х нужно воспользоваться равенством
для отрицательных х нужно воспользоваться равенством 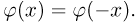
Интегральная теорема Муавра-Лапласа:
Если в схеме Бернулли число испытаний п велико, то для вероятности 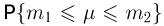 того, что число успехов
того, что число успехов 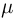 заключено в пределах от
заключено в пределах от 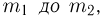 справедливо приближенное соотношение (интегральная формула Муавра-Лапласа)
справедливо приближенное соотношение (интегральная формула Муавра-Лапласа)
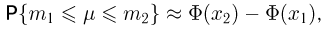
где 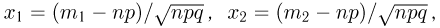
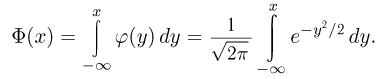
Доказательство теоремы проведем, опираясь на локальную теорему Муавра-Лапласа (здесь мы также опускаем отдельные технические детали доказательства). Если 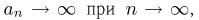 то в силу теоремы о среднем и равномерной непрерывности функции
то в силу теоремы о среднем и равномерной непрерывности функции 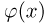
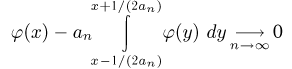
равномерно по х. Поэтому, полагая 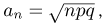 из локальной теоремы Муавра-Лапласа находим
из локальной теоремы Муавра-Лапласа находим
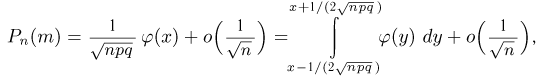
где 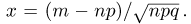 Суммируя по всем
Суммируя по всем 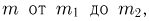 окончательно получаем
окончательно получаем
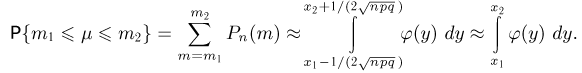
Тем самым утверждение теоремы доказано.
Отметим, что интегральная теорема Муавра-Лапласа является следствием более общей центральной предельной теоремы, которую мы докажем другим, более простым способом в гл. 8.
Функция 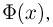 фигурирующая в интегральной формуле Муавра-Лапласа, носит название функции стандартного нормального, или гауссова, распределения. В силу четности
фигурирующая в интегральной формуле Муавра-Лапласа, носит название функции стандартного нормального, или гауссова, распределения. В силу четности 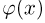 функция стандартного нормального распределения обладает свойством
функция стандартного нормального распределения обладает свойством 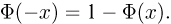 Поэтому в табл. 3 приложения приведены значения не
Поэтому в табл. 3 приложения приведены значения не 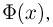 а интеграла Лапласа
а интеграла Лапласа 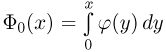 и только для положительных х. Ясно, что
и только для положительных х. Ясно, что 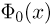 является нечетной функцией, т.е.
является нечетной функцией, т.е. 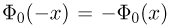 и, кроме того,
и, кроме того, 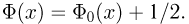 В терминах интеграла Лапласа интегральная формула Муавра-Лапласа имеет вид
В терминах интеграла Лапласа интегральная формула Муавра-Лапласа имеет вид
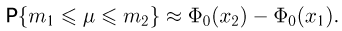
Именно этой формулой мы будем пользоваться при расчетах в примерах следующего параграфа.
Замечание. Распределение Пуассона, плотность и функция стандартного нормального распределения играют в приложениях столь существенную роль, что таблицы их значений содержатся практически в любом справочнике, учебнике или задачнике по теории вероятностей или математической статистике (см. также приложение). Однако следует еще раз обратить внимание на то, что довольно часто в таблицах приводятся не значения функции стандартного нормального распределения, а значения интеграла Лапласа 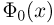 или даже функции
или даже функции 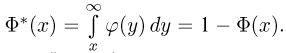 Поэтому, прежде чем пользоваться таблицей, необходимо внимательно посмотреть, значения какой функции даны в этой таблице.
Поэтому, прежде чем пользоваться таблицей, необходимо внимательно посмотреть, значения какой функции даны в этой таблице.
Применение приближенных формул Пуассона и Муавра-Лапласа
В этом параграфе мы дадим некоторые рекомендации (носящие, вообще говоря, условный характер) по применению приближенных формул и рассмотрим примеры расчетов с их помощью.
Если число испытаний 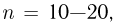 то приближенные формулы используются для грубых прикидочных расчетов. При этом формула Пуассона применяется в том случае, когда
то приближенные формулы используются для грубых прикидочных расчетов. При этом формула Пуассона применяется в том случае, когда 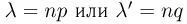 изменяются в пределах от 0—2 (при п = 10) до 0—3 (при п = 20); в противном случае необходимо пользоваться формулами Муавра-Лапласа.
изменяются в пределах от 0—2 (при п = 10) до 0—3 (при п = 20); в противном случае необходимо пользоваться формулами Муавра-Лапласа.
Если 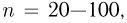 то приближенные формулы уже можно использовать для прикладных инженерных расчетов. Формулу Пуассона рекомендуется применять, когда
то приближенные формулы уже можно использовать для прикладных инженерных расчетов. Формулу Пуассона рекомендуется применять, когда 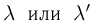 заключены в следующих пределах:
заключены в следующих пределах: 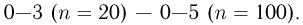
Если п = 100—1000, то практически при любых инженерных расчетах можно обойтись приближенными формулами. Формула Пуассона используется, когда 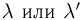 изменяются в следующих пределах: 0—5
изменяются в следующих пределах: 0—5 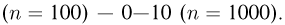
Наконец, при п > 1000 даже специальные таблицы рассчитываются с помощью приближенных формул (правда, для увеличения точности используют специальные поправки). В этом случае для применения формулы Пуассона необходимо, чтобы 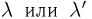 лежали в пределах 0—10 и более.
лежали в пределах 0—10 и более.
Прежде чем переходить к рассмотрению примеров, скажем несколько слов о погрешностях, возникающих при использовании приближенных формул. Для этого отметим, что знак 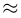 приближенного равенства использовался нами в том смысле, что при увеличении п разность между величинами, связанными этим знаком, стремится к нулю. Иными словами, приближенные формулы гарантируют только малую абсолютную погрешность, но относительная погрешность, т. е. отношение величин, связанных знаком
приближенного равенства использовался нами в том смысле, что при увеличении п разность между величинами, связанными этим знаком, стремится к нулю. Иными словами, приближенные формулы гарантируют только малую абсолютную погрешность, но относительная погрешность, т. е. отношение величин, связанных знаком 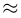 может быть сколь угодно большой. Так, при использовании формулы Пуассона для вычисления биномиальных вероятностей
может быть сколь угодно большой. Так, при использовании формулы Пуассона для вычисления биномиальных вероятностей 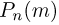 относительная погрешность имеет тенденцию к увеличению с ростом т. Аналогично, в формулах Муавра-Лапласа относительная погрешность увеличивается с ростом абсолютного значения
относительная погрешность имеет тенденцию к увеличению с ростом т. Аналогично, в формулах Муавра-Лапласа относительная погрешность увеличивается с ростом абсолютного значения 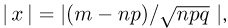 причем в интегральной формуле Муавра-Лапласа такое увеличение происходит только в том случае, когда
причем в интегральной формуле Муавра-Лапласа такое увеличение происходит только в том случае, когда 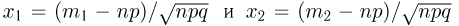 имеют одинаковый знак. Читатель сможет убедиться в этом из рассмотренных ниже примеров.
имеют одинаковый знак. Читатель сможет убедиться в этом из рассмотренных ниже примеров.
Следует отметить, что к настоящему времени доказаны теоремы, позволяющие не только получать более точные приближения биномиальных вероятностей 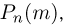 но и оценивать возникающие при этом погрешности. Однако эти результаты довольно сложны и весьма редко используются в инженерной практике.
но и оценивать возникающие при этом погрешности. Однако эти результаты довольно сложны и весьма редко используются в инженерной практике.
Пример:
Счетчик регистрирует попадающие в него частицы с вероятностью р = 0,9. Найдем вероятность 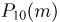 того, что он зарегистрировал
того, что он зарегистрировал 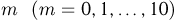 частиц при условии, что в него попало 10 частиц.
частиц при условии, что в него попало 10 частиц.
Воспользуемся сначала точной формулой Бернулли, в соответствии с которой 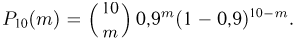 Результаты расчетов приведены в табл. ! в графе «Точное значение
Результаты расчетов приведены в табл. ! в графе «Точное значение 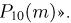
Постараемся применить теперь приближенные формулы. В нашем случае 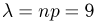 велико, однако
велико, однако 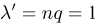 мало и, значит, рекомендации советуют воспользоваться формулой Пуассона, но по отношению к незарегистрированным частицам. В соответствии с этой формулой
мало и, значит, рекомендации советуют воспользоваться формулой Пуассона, но по отношению к незарегистрированным частицам. В соответствии с этой формулой
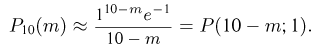
По табл. 1 приложения находим
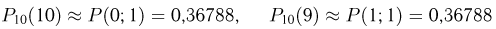
и т.д. Приближенные значения приведены в табл. 1 в графе «Значение, вычисленное по формуле Пуассона». Для сравнения полученных результатов в эту же таблицу включена графа «Погрешность». Анализируя приведенные в этой графе числа, видим, что максимальная абсолютная погрешность 0.01954 невелика, чего нельзя сказать о максимальной относительной погрешности. В частности, приближенное значение 0.00051 вероятности 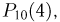 вычисленное по формуле Пуассона, почти в 4 раза больше истинного значения 0,00014 этой вероятности.
вычисленное по формуле Пуассона, почти в 4 раза больше истинного значения 0,00014 этой вероятности.
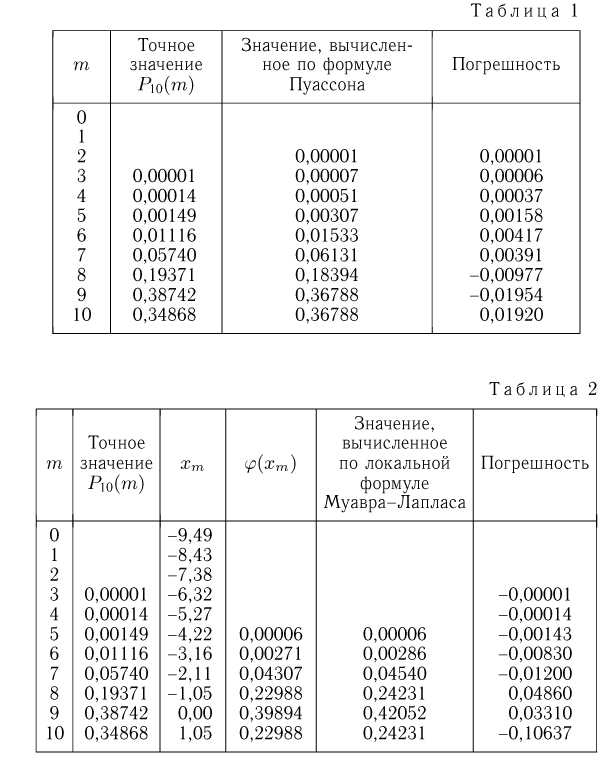
Наконец, покажем, как воспользоваться локальной формулой Муавра-Лапласа, хотя здесь это и не рекомендуется делать. Тогда 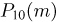 мы должны заменить числом
мы должны заменить числом 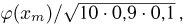 где
где 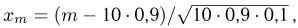 а
а 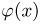 — плотность стандартного нормального распределения. Результаты вычислений с использованием табл. 2 приложения приведены в табл. 2. Как и следовало ожидать, локальная формула Муавра-Лапласа дает существенно большие погрешности.
— плотность стандартного нормального распределения. Результаты вычислений с использованием табл. 2 приложения приведены в табл. 2. Как и следовало ожидать, локальная формула Муавра-Лапласа дает существенно большие погрешности.
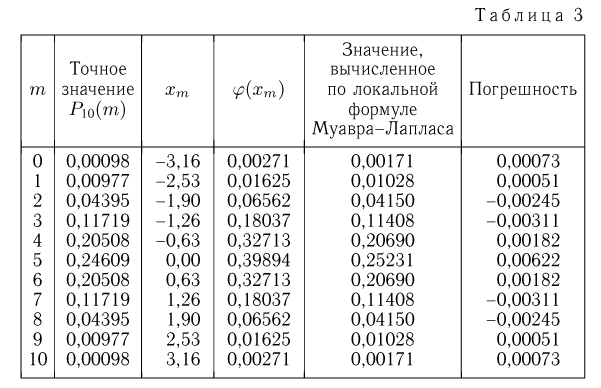
Пример:
Производится 10 подбрасываний симметричной монеты. Найдем вероятность того, что выпадет ровно 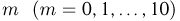 «гербов».
«гербов».
Так же, как и в предыдущем примере, сначала по формуле Бернулли 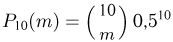 вычислим точные значения этих вероятностей (см. табл. 3, графа «Точное значение
вычислим точные значения этих вероятностей (см. табл. 3, графа «Точное значение 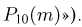
Воспользуемся теперь приближенными формулами. В данном примере 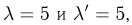 поэтому применим формулу Муавра-Лапласа. Так как нас интересует вероятность выпадения ровно т «гербов», то необходимо применить локальную формулу Муавра-Лапласа, в которой
поэтому применим формулу Муавра-Лапласа. Так как нас интересует вероятность выпадения ровно т «гербов», то необходимо применить локальную формулу Муавра-Лапласа, в которой
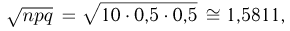
и для m«гербов»
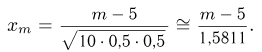
Результаты вычислений также приведены в табл. 3. Из табл. 3 видно, что и в этом случае максимальная абсолютная погрешность 0,00622 по отношению к максимальному значению 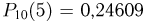 вероятности
вероятности 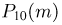 достаточно мала.
достаточно мала.
Читателю советуем самостоятельно применить формулу Пуассона и убедиться в том, что она дает существенно большие погрешности.
Пример:
В тираже «Спортлото 6 из 49» участвуют 10000000 карточек. Найдем вероятность события А — хотя бы в одной из этих карточек зачеркнуты 6 выигрышных номеров (максимальный выигрыш). Естественно сразу же перейти к дополнительному событию 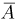 — ни на одну карточку не выпадет максимальный выигрыш. Считая, что в каждой из карточек номера зачеркиваются случайным образом и независимо от остальных, видим, что число карточек, на которые выпал максимальный выигрыш, подчиняется биномиальному закону с параметрами
— ни на одну карточку не выпадет максимальный выигрыш. Считая, что в каждой из карточек номера зачеркиваются случайным образом и независимо от остальных, видим, что число карточек, на которые выпал максимальный выигрыш, подчиняется биномиальному закону с параметрами 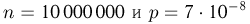 (см. пример 7 в гл. 2). Поскольку
(см. пример 7 в гл. 2). Поскольку 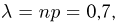 то для определения вероятности
то для определения вероятности 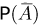 воспользуемся формулой Пуассона. Тогда
воспользуемся формулой Пуассона. Тогда 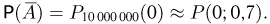 Из табл. 1 приложения имеем
Из табл. 1 приложения имеем 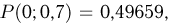 и, значит,
и, значит, 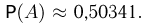 Таким образом, вероятность того, что хотя бы одна из 10000000 карточек окажется выигрышной, чуть больше 1/2.
Таким образом, вероятность того, что хотя бы одна из 10000000 карточек окажется выигрышной, чуть больше 1/2.
Пример:
Для определения числа 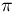 экспериментальным путем (см. пример 12 в гл.2) производится
экспериментальным путем (см. пример 12 в гл.2) производится 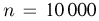 бросаний иглы длиной
бросаний иглы длиной 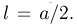 Значение
Значение 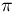 определяется при этом формулой
определяется при этом формулой 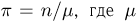 — число пересечений иглой одной из прямых. Найдем вероятность того, что определенное таким образом приближенное значение
— число пересечений иглой одной из прямых. Найдем вероятность того, что определенное таким образом приближенное значение 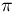 будет заключено в пределах от 3,14 до 3,15 (событие А). Событие А происходит тогда и только тогда, когда число пересечений будет лежать в пределах от
будет заключено в пределах от 3,14 до 3,15 (событие А). Событие А происходит тогда и только тогда, когда число пересечений будет лежать в пределах от 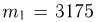 до
до 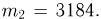 Вероятность успеха (пересечения иглой одной из прямых при
Вероятность успеха (пересечения иглой одной из прямых при 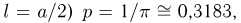 неудачи
неудачи 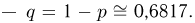 Поскольку п, пр и nq велики, а по условию задачи нас интересует вероятность попадания на интервал, воспользуемся интегральной формулой Муавра-Лапласа, в которой
Поскольку п, пр и nq велики, а по условию задачи нас интересует вероятность попадания на интервал, воспользуемся интегральной формулой Муавра-Лапласа, в которой 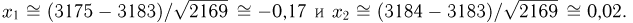
По табл.3 приложения получаем, что 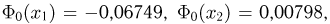 и, значит,
и, значит, 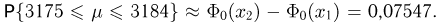 Отсюда можно сделать вывод: 10000 бросаний иглы явно мало для того, чтобы определенное экспериментально число
Отсюда можно сделать вывод: 10000 бросаний иглы явно мало для того, чтобы определенное экспериментально число 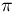 с достаточно большой вероятностью лежало в пределах от 3,14 до 3,15.
с достаточно большой вероятностью лежало в пределах от 3,14 до 3,15.
Пример:
В сосуде содержится 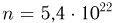 молекул газа. В некоторый момент времени сосуд делят непроницаемой перегородкой на две части одинаковых объемов. Считая, что каждая молекула с одинаковой вероятностью
молекул газа. В некоторый момент времени сосуд делят непроницаемой перегородкой на две части одинаковых объемов. Считая, что каждая молекула с одинаковой вероятностью 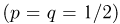 может находиться в любой из двух частей, определим вероятность события А — в одной из частей сосуда будет содержаться молекул по крайней мере на
может находиться в любой из двух частей, определим вероятность события А — в одной из частей сосуда будет содержаться молекул по крайней мере на 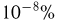 (от общего числа молекул в сосуде) больше, чем в другой. Перейдем к дополнительному событию
(от общего числа молекул в сосуде) больше, чем в другой. Перейдем к дополнительному событию 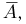 которое, как нетрудно видеть, состоит в том, что число молекул в первой части сосуда заключено в пределах от
которое, как нетрудно видеть, состоит в том, что число молекул в первой части сосуда заключено в пределах от 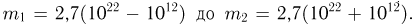 Поскольку п весьма велико, а
Поскольку п весьма велико, а 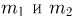 различны, воспользуемся интегральной формулой Муавра-Лапласа, в которой
различны, воспользуемся интегральной формулой Муавра-Лапласа, в которой 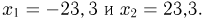 Следовательно,
Следовательно, 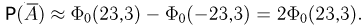 В табл.3 приложения, как и в большинстве других таблиц, значения функции
В табл.3 приложения, как и в большинстве других таблиц, значения функции 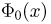 приводятся для х, не превосходящих 5. Учитывая монотонное возрастание функции
приводятся для х, не превосходящих 5. Учитывая монотонное возрастание функции 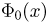 можно сделать следующую оценку для вероятности
можно сделать следующую оценку для вероятности 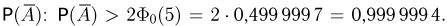 Значит,
Значит, 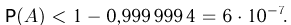 Более точные расчеты показывают, что
Более точные расчеты показывают, что 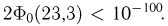 Как мы видим, вероятность числу молекул в одной части сосуда отличаться от числа молекул в другой даже на
Как мы видим, вероятность числу молекул в одной части сосуда отличаться от числа молекул в другой даже на 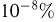 ничтожно мала.
ничтожно мала.
Пример:
Определим, какое число п подбрасываний симметричной монеты надо произвести, чтобы наблюденная частота 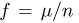 выпадения «герба» отличалась от вероятности
выпадения «герба» отличалась от вероятности 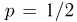 выпадения «герба» не более чем на 0,01 с вероятностью 0.99. Предположим, что мы произвели п испытаний. Тогда число
выпадения «герба» не более чем на 0,01 с вероятностью 0.99. Предположим, что мы произвели п испытаний. Тогда число 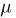 выпадений «герба» должно быть заключено в пределах от
выпадений «герба» должно быть заключено в пределах от 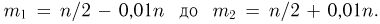 Воспользуемся интегральной формулой Муавра-Лапласа, в которой
Воспользуемся интегральной формулой Муавра-Лапласа, в которой 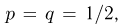
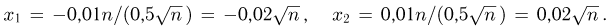
Тогда 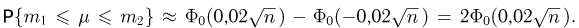 Поскольку из условия задачи известно, что
Поскольку из условия задачи известно, что 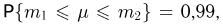 то получаем
то получаем 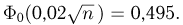 Из табл. 3 приложения находим
Из табл. 3 приложения находим 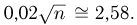 Отсюда следует, что
Отсюда следует, что 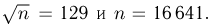 Таким образом, необходимо произвести около 17000 подбрасываний.
Таким образом, необходимо произвести около 17000 подбрасываний.
Определим теперь, сколько нужно произвести подбрасываний симметричной монеты, чтобы частота выпадения «герба» отличалась от вероятности не более чем на 0,005 (а не на 0,01) с той же вероятностью 0,99. Иными словами, считая, что наблюденная частота 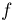 выпадения «герба» является оценкой вероятности р = 1/2 выпадения «герба», мы хотим узнать, во сколько раз нужно увеличить число испытаний, чтобы повысить точность оценки в два раза. Производя аналогичные вычисления, получаем
выпадения «герба» является оценкой вероятности р = 1/2 выпадения «герба», мы хотим узнать, во сколько раз нужно увеличить число испытаний, чтобы повысить точность оценки в два раза. Производя аналогичные вычисления, получаем 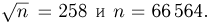 Значит, число подбрасываний нужно увеличить в 4 раза. Если бы мы захотели повысить точность оценки в 3 раза, то нам пришлось бы увеличить число подбрасываний уже в 9 раз. Нетрудно видеть, что выведенный закон присущ схеме Бернулли с любой вероятностью успеха р: оценивая вероятность р с помощью наблюденной частоты
Значит, число подбрасываний нужно увеличить в 4 раза. Если бы мы захотели повысить точность оценки в 3 раза, то нам пришлось бы увеличить число подбрасываний уже в 9 раз. Нетрудно видеть, что выведенный закон присущ схеме Бернулли с любой вероятностью успеха р: оценивая вероятность р с помощью наблюденной частоты 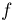 для улучшения оценки в а раз мы должны увеличить число наблюдений в
для улучшения оценки в а раз мы должны увеличить число наблюдений в 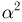 раз.
раз.
Теорема Бернулли
Предположим, что мы произвели большое число п испытаний Бернулли с вероятностью успеха р. По числу полученных успехов 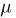 определим наблюденную частоту
определим наблюденную частоту 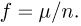 Спрашивается, как сильно может отличаться наблюденная частота успеха
Спрашивается, как сильно может отличаться наблюденная частота успеха 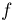 от вероятности успеха р? Ясно, что, вообще говоря, частота
от вероятности успеха р? Ясно, что, вообще говоря, частота 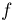 может принимать любые значения от 0 до 1. Так, мы вполне можем получить в n испытаниях одни неудачи. Но, как мы знаем, вероятность такого события равна
может принимать любые значения от 0 до 1. Так, мы вполне можем получить в n испытаниях одни неудачи. Но, как мы знаем, вероятность такого события равна 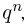 и при больших n она будет весьма мала. Поэтому естественно ожидать, что при больших n частота
и при больших n она будет весьма мала. Поэтому естественно ожидать, что при больших n частота 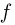 с большой вероятностью группируется вокруг вероятности р, что мы сейчас и установим, исходя из интегральной теоремы Муавра-Лапласа.
с большой вероятностью группируется вокруг вероятности р, что мы сейчас и установим, исходя из интегральной теоремы Муавра-Лапласа.
Пусть 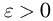 — любое сколь угодно малое число, а событие А заключается в том, что наблюдаемая в п испытаниях частота
— любое сколь угодно малое число, а событие А заключается в том, что наблюдаемая в п испытаниях частота 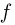 отличается от вероятности по модулю не больше чем на
отличается от вероятности по модулю не больше чем на 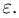 Иными словами, событие А происходит тогда и только тогда, когда число успехов в п испытаниях заключено в пределах от
Иными словами, событие А происходит тогда и только тогда, когда число успехов в п испытаниях заключено в пределах от 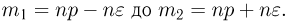 Теперь, если п велико, то мы можем воспользоваться интегральной теоремой Муавра-Лапласа, в которой
Теперь, если п велико, то мы можем воспользоваться интегральной теоремой Муавра-Лапласа, в которой 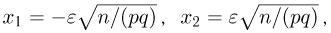 и, значит,
и, значит,
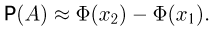
Но с ростом 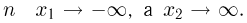 В свою очередь,
В свою очередь, 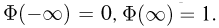 Поэтому, каково бы ни было
Поэтому, каково бы ни было 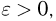 с ростом п вероятность того, что частота
с ростом п вероятность того, что частота 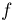 отличается от вероятности р не более чем на
отличается от вероятности р не более чем на 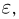 стремится к 1.
стремится к 1.
Установленный нами факт предельного постоянства частоты впервые был обнаружен Я. Бернулли, он носит название (слабого) закона больших чисел или теоремы Бернулли. Закон больших чисел и его многочисленные обобщения являются звеном, позволяющим связать аксиоматическое построение теории вероятностей с эмпирическим законом постоянства частоты, с которого мы начали путешествие в теорию вероятностей. Именно он позволяет обосновать то широкое применение методов теории вероятностей на практике, которое мы имеем в настоящее время.
Однако если произвести более строгий логический анализ, то окажется, что слабый закон больших чисел также не вполне удовлетворяет нашим исходным предпосылкам, поскольку когда мы говорим о стабильности частоты, то имеем в виду процесс, протекающий во времени. Слабый закон больших чисел утверждает только, что при большом, но фиксированном числе испытаний частота мало отличается от вероятности. Слабый закон больших чисел еще не исключает значительных, но редких отклонений частоты от вероятности при последовательном проведении испытаний. Здесь мы пока только отметим, что имеет место усиленный закон больших чисел, который в определенной степени устраняет это логическое несовершенство слабого закона больших чисел.
Более подробно закон больших чисел, как и интегральная теорема Муавра-Лапласа, будут обсуждены нами в гл. 8, посвященной предельным теоремам теории вероятностей.
Вычисление определенных интегралов методом Монте-Карло
В этом параграфе мы рассмотрим применение предельных теорем для вычисления многократных интегралов.
Начнем с повторения материала, излагаемого в любом курсе математического анализа.
Пусть непрерывная элементарная (т. е. выраженная в элементарных функциях) функция 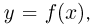 заданная на отрезке
заданная на отрезке 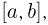 ограничена снизу и сверху числами с и С соответственно, и необходимо вычислить определенный интеграл
ограничена снизу и сверху числами с и С соответственно, и необходимо вычислить определенный интеграл 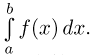 Поскольку линейные замены
Поскольку линейные замены 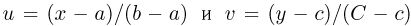 приводят к интегрированию функции, заданной на отрезке [0, 1] и ограниченной снизу нулем и сверху единицей, то в дальнейшем будем считать, что
приводят к интегрированию функции, заданной на отрезке [0, 1] и ограниченной снизу нулем и сверху единицей, то в дальнейшем будем считать, что  и
и 
Для вычисления определенного интеграла 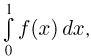 как должно быть известно читателю, необходимо сначала найти какую-либо первообразную F(x) функции
как должно быть известно читателю, необходимо сначала найти какую-либо первообразную F(x) функции 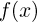 и затем воспользоваться формулой Ньютона-Лейбница, согласно которой
и затем воспользоваться формулой Ньютона-Лейбница, согласно которой 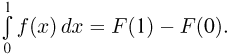 Однако хорошо известно и то, что интеграл далеко не от всякой элементарной функции
Однако хорошо известно и то, что интеграл далеко не от всякой элементарной функции 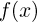 может быть выражен также в элементарных функциях. Тем не менее к настоящему времени разработаны методы приближенного численного интегрирования (простейшими из них являются формулы трапеций и Симпсона), для применения которых нужно вычислить значения функции
может быть выражен также в элементарных функциях. Тем не менее к настоящему времени разработаны методы приближенного численного интегрирования (простейшими из них являются формулы трапеций и Симпсона), для применения которых нужно вычислить значения функции 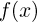 в определенных точках
в определенных точках  (узлах интегрирования) и затем сложить полученные результаты с некоторыми весовыми коэффициентами. Обычно для достижения требуемой точности достаточно взять весьма небольшое число т узлов интегрирования. Пусть, например, m = 10. Тогда, даже если
(узлах интегрирования) и затем сложить полученные результаты с некоторыми весовыми коэффициентами. Обычно для достижения требуемой точности достаточно взять весьма небольшое число т узлов интегрирования. Пусть, например, m = 10. Тогда, даже если 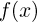 задается сложным аналитическим выражением, современная ЭВМ легко справится с поставленной задачей и почти мгновенно подсчитает значение определенного интеграла.
задается сложным аналитическим выражением, современная ЭВМ легко справится с поставленной задачей и почти мгновенно подсчитает значение определенного интеграла.
Усложним задачу и предположим, что нужно вычислить k-кратный интеграл 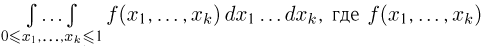 так же заключена между 0 и 1. Теперь уже для применения численных методов необходимо взять т узлов интегрирования
так же заключена между 0 и 1. Теперь уже для применения численных методов необходимо взять т узлов интегрирования  для каждой переменной интегрирования
для каждой переменной интегрирования 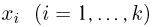 и найти значения функции
и найти значения функции  для всех комбинаций
для всех комбинаций  (общих узлов интегрирования). Поскольку
(общих узлов интегрирования). Поскольку 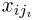 для каждого i может принимать т различных значений, то всего общих узлов интегрирования будет
для каждого i может принимать т различных значений, то всего общих узлов интегрирования будет 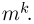
В частности, если т= 10, то для вычисления 10-кратного интеграла необходимо подсчитать значения 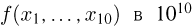 точках, что представляет собой уже весьма трудоемкую задачу даже для самых современных ЭВМ.
точках, что представляет собой уже весьма трудоемкую задачу даже для самых современных ЭВМ.
Попробуем теперь решить те же самые задачи, привлекая вероятностные соображения. Для этого снова вернемся к однократному интегралу 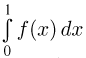 и вспомним, что геометрически он представляет собой площадь области А, ограниченной графиком функции
и вспомним, что геометрически он представляет собой площадь области А, ограниченной графиком функции 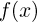 (рис. 1).
(рис. 1).
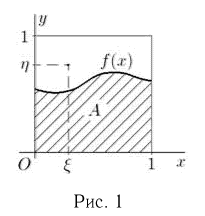
Проведем опыт, заключающийся в бросании случайным образом (т. е. в соответствии с принципом геометрической вероятности) двух точек на отрезок 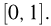 Обозначим координату одной из них через
Обозначим координату одной из них через 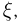 а другой — через
а другой — через 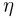 и отложим
и отложим 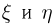 по осям абсцисс и ординат соответственно (см. рис. 1). Проверим выполнение неравенства
по осям абсцисс и ординат соответственно (см. рис. 1). Проверим выполнение неравенства 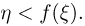 Справедливость этого неравенства означает, что точка
Справедливость этого неравенства означает, что точка 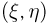 попала в область А. Но в соответствии с принципом геометрической вероятности вероятность Р(А) попадания точки
попала в область А. Но в соответствии с принципом геометрической вероятности вероятность Р(А) попадания точки 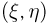 в область А есть отношение площади А к площади единичного квадрата, т.е.
в область А есть отношение площади А к площади единичного квадрата, т.е. 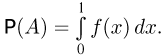
Повторим описанный выше опыт п раз и по результатам наблюдений определим частоту 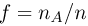 появления события А, т.е. попадания точки
появления события А, т.е. попадания точки 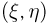 в область А. Поскольку по теореме Бернулли частота
в область А. Поскольку по теореме Бернулли частота 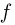 с ростом п стремится к вероятности Р(А), то, подставляя вместо вероятности Р(А) ее значение, получаем приближенное равенство
с ростом п стремится к вероятности Р(А), то, подставляя вместо вероятности Р(А) ее значение, получаем приближенное равенство
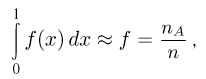
которое и служит для оценки интеграла по результатам случайных испытаний.
Описанный метод приближенного вычисления определенного интеграла носит название метода статистических испытаний или метода Монте-Карло (город Монте-Карло — место сосредоточения всемирно известных игорных домов). Название «метод Монте-Карло» связано с тем, что проводимые испытания очень напоминают подбрасывание монеты, бросание игральной кости или игру в рулетку.
Имеется существенное качественное различие между погрешностями, возникающими при применении методов численного интегрирования и метода Монте-Карло. В первом случае при выполнении соответствующих условий можно дать гарантированную оценку точности, т.е. указать достоверные границы, в которых обязательно будет заключено истинное значение вычисляемого интеграла. Во втором случае гарантированную оценку нельзя дать в принципе, а можно сказать только, что отклонение значения интеграла, вычисленного методом Монте-Карло, от истинного значения этого же интеграла не превосходит некоторой величины с определенной вероятностью.
Для определения количественного значения погрешности при применении метода Монте-Карло обычно пользуются интегральной формулой Муавра-Лапласа. Пусть истинное значение интеграла
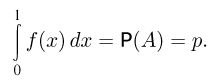
Тогда для заданного 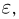 событие {приближенное значение
событие {приближенное значение 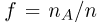 интеграла удовлетворяет неравенству
интеграла удовлетворяет неравенству 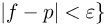 совпадает с событием {число успехов п в схеме Вернул ли с вероятностью успеха р удовлетворяет неравенству
совпадает с событием {число успехов п в схеме Вернул ли с вероятностью успеха р удовлетворяет неравенству 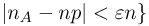 или, что то же самое, с событием {число успехов
или, что то же самое, с событием {число успехов 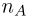 заключено в пределах от
заключено в пределах от 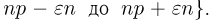 Воспользовавшись теперь интегральной формулой Муавра-Лапласа, получаем, что вероятность
Воспользовавшись теперь интегральной формулой Муавра-Лапласа, получаем, что вероятность 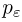 того, что значение интеграла
того, что значение интеграла 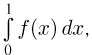 вычисленного методом Монте-Карло, отличается от истинного значения р этого интеграла не более чем на
вычисленного методом Монте-Карло, отличается от истинного значения р этого интеграла не более чем на 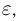 задается выражением
задается выражением
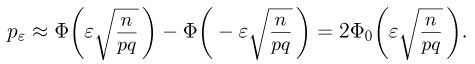
Из последней формулы видно, что если мы хотим уменьшить погрешность  раз с сохранением той же вероятности
раз с сохранением той же вероятности  то мы должны произвести в
то мы должны произвести в  раз больше опытов (см. пример 8).
раз больше опытов (см. пример 8).
При вычислении вероятности 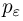 часто возникает затруднение, связанное с тем, что значение р нам неизвестно. В этом случае обычно идут двумя путями. Первый путь заключается в том, что величина pq заменяется ее верхней оценкой 1/4. Второй путь состоит в замене в формуле для
часто возникает затруднение, связанное с тем, что значение р нам неизвестно. В этом случае обычно идут двумя путями. Первый путь заключается в том, что величина pq заменяется ее верхней оценкой 1/4. Второй путь состоит в замене в формуле для 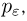 вероятности р ее приближенным значением
вероятности р ее приближенным значением 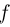 .
.
Более точную оценку погрешности при применении метода Монте-Карло можно получить на основе результатов математической статистики (раздел «Доверительные интервалы»).
Метод Монте-Карло очевидным образом переносится и на тот случай, когда нужно вычислить k-кратный интеграл
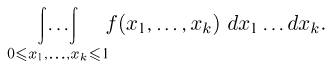
Единственное отличие заключается в том, что на отрезок [0, 1] необходимо бросать уже не две, а k+ 1 точек 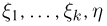 и проверять выполнение неравенства
и проверять выполнение неравенства 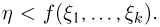 Все остальные результаты, в том числе окончательное выражение
Все остальные результаты, в том числе окончательное выражение
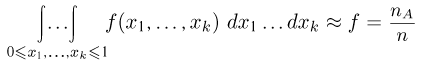
для приближенного значения интеграла и формула для оценки вероятности ре погрешности, полностью сохраняются и в этом случае.
Естественно, возникает вопрос: в каких случаях следует применять методы численного интегрирования, а в каких — метод Монте-Карло? Для этого вернемся к началу параграфа и снова предположим, что для достижения заданной точности вычисления однократного интеграла необходимо взять т= 10 узлов интегрирования 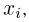 т.е. фактически произвести 10 «обобщенных» операций, состоящих в определении
т.е. фактически произвести 10 «обобщенных» операций, состоящих в определении 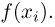 Опыт показывает (см. также пример 8), что для достижения аналогичной точности методом Монте-Карло требуются десятки, а то и сотни тысяч испытаний. Пусть для определенности необходимое число испытаний
Опыт показывает (см. также пример 8), что для достижения аналогичной точности методом Монте-Карло требуются десятки, а то и сотни тысяч испытаний. Пусть для определенности необходимое число испытаний 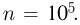 Поскольку, как правило, основное время при вычислениях занимает нахождение значения
Поскольку, как правило, основное время при вычислениях занимает нахождение значения 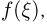 то трудоемкость метода Монте-Карло оценивается
то трудоемкость метода Монте-Карло оценивается 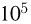 «обобщенными» операциями, т.е. метод Монте-Карло существенно уступает численным методам. Перейдем к вычислению интеграла кратности k. Тогда, как мы уже говорили, при применении численных методов трудоемкость вычислений составит уже
«обобщенными» операциями, т.е. метод Монте-Карло существенно уступает численным методам. Перейдем к вычислению интеграла кратности k. Тогда, как мы уже говорили, при применении численных методов трудоемкость вычислений составит уже 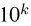 операций. Однако использование метода Монте-Карло ведет лишь к незначительному увеличению трудоемкости. В частности, при вычислении 5-кратного интеграла трудоемкость обоих методов практически совпадает, а при вычислении интегралов большей кратности численные методы уже начинают проигрывать методу Монте-Карло, причем тем больше, чем больше кратность интеграла.
операций. Однако использование метода Монте-Карло ведет лишь к незначительному увеличению трудоемкости. В частности, при вычислении 5-кратного интеграла трудоемкость обоих методов практически совпадает, а при вычислении интегралов большей кратности численные методы уже начинают проигрывать методу Монте-Карло, причем тем больше, чем больше кратность интеграла.
Резюмируя изложенное выше, можно сказать, что применение метода Монте-Карло оправдано только при вычислении кратных интегралов, причем в случае большой кратности метод Монте-Карло просто не имеет конкурентов со стороны методов численного интегрирования.
К достоинствам метода Монте-Карло можно отнести и то, что погрешность при вычислении интеграла с его помощью вообще не зависит от свойств гладкости функции 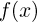 в то время как для получения заданной точности при численном интегрировании необходимо выполнение ограничений на производные функции
в то время как для получения заданной точности при численном интегрировании необходимо выполнение ограничений на производные функции 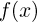 В частности, метод Монте-Карло с одинаковым успехом применим для интегрирования как непрерывных функций, так и функций, терпящих разрывы.
В частности, метод Монте-Карло с одинаковым успехом применим для интегрирования как непрерывных функций, так и функций, терпящих разрывы.
Конечно, при вычислении интегралов методом Монте-Карло никто не производит физического бросания точки на отрезок. Для этой цели служат специальные программы или датчики случайных или, точнее говоря, «псевдослучайных» чисел.
Следует обратить внимание на то, что метод Монте-Карло не позволяет беспредельно уменьшать погрешность вычислений. И дело здесь даже не в том, что необходимо проводить очень большое число испытаний. «Псевдослучайные» числа, как вытекает из их названия, не удовлетворяют полностью свойству случайности. Поэтому, прежде чем использовать какой-либо датчик «псевдослучайных» чисел, обычно производят многочисленные проверки (на отсутствие периодичности, на равномерность, на независимость и т.д.) с помощью различных критериев. Однако даже выдержавшие самые строгие проверки датчики генерируют числа, которые не могут быть отнесены к разряду «случайных» в полном смысле этого слова.
Полиномиальная схема
В заключение скажем несколько слов о так называемой полиномиальной схеме. Если схема Бернулли интерпретируется как подбрасывание несимметричной монеты, то полиномиальную схему можно трактовать как обобщение статистики Максвелла-Больцмана на тот случай, когда вероятности попадания каждой частицы в различные ячейки неодинаковы. Итак, предположим, что опыт состоит из п независимых одинаковых испытаний, в каждом из которых может произойти одно и только одно из m несовместных событий 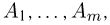 причем событие
причем событие 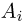 наступает с вероятностью
наступает с вероятностью 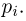 Тогда вероятность
Тогда вероятность 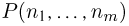 того, что в п испытаниях событие
того, что в п испытаниях событие 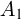 произойдет ровно
произойдет ровно 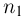 раз…, событие
раз…, событие 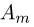 произойдет ровно
произойдет ровно 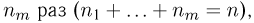 определяется выражением
определяется выражением
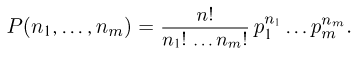
Последняя формула носит название полиномиального распределения. Ее вывод аналогичен выводу формулы Бернулли с учетом комбинаторных соотношений, используемых при рассмотрении статистики Максвелла-Больцмана, и любознательный читатель вполне может провести его самостоятельно. Полиномиальную вероятность  можно получить также как коэффициент при
можно получить также как коэффициент при 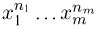 в разложении полинома
в разложении полинома 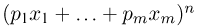 в ряд по степеням
в ряд по степеням 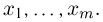
Полиномиальная схема обладает теми же предельными свойствами, что и схема Бернулли. Так, если устремить п к бесконечности, то вероятность  приближенно вычисляется с помощью так называемой многомерной нормальной плотности. Вводя в рассмотрение вектор
приближенно вычисляется с помощью так называемой многомерной нормальной плотности. Вводя в рассмотрение вектор 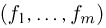 наблюденных частот появлений событий
наблюденных частот появлений событий 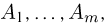 можно доказать, что при большом числе испытаний п этот вектор мало отличается от вектора вероятностей
можно доказать, что при большом числе испытаний п этот вектор мало отличается от вектора вероятностей 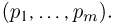
Пример:
В магазине висит 1 костюм второго роста, 2 костюма третьего роста, 3 костюма четвертого роста. Костюм второго роста спрашивается с вероятностью 0,2, костюм третьего роста — с вероятностью 0,3, костюм четвертого роста — с вероятностью 0,5. В магазин обратились 3 покупателя. Найдем вероятность того, что хотя бы один из них ушел без покупки (событие А). Представим событие А в виде суммы несовместных событий:
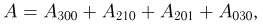
где 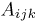 означает, что i покупателей спросили костюм второго роста, j — третьего роста и k — четвертого. Воспользовавшись теперь полиномиальным распределением, получаем
означает, что i покупателей спросили костюм второго роста, j — третьего роста и k — четвертого. Воспользовавшись теперь полиномиальным распределением, получаем
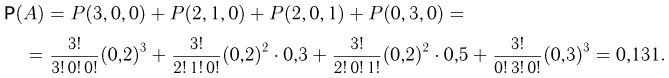
Таким образом, искомая вероятность 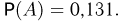
Решение заданий и задач по предметам:
Дополнительные лекции по теории вероятностей:
- Случайные события и их вероятности
- Случайные величины
- Функции случайных величин
- Числовые характеристики случайных величин
- Законы больших чисел
- Статистические оценки
- Статистическая проверка гипотез
- Статистическое исследование зависимостей
- Теории игр
- Вероятность события
- Теорема умножения вероятностей
- Формула полной вероятности
- Теорема о повторении опытов
- Нормальный закон распределения
- Определение законов распределения случайных величин на основе опытных данных
- Системы случайных величин
- Нормальный закон распределения для системы случайных величин
- Вероятностное пространство
- Классическое определение вероятности
- Геометрическая вероятность
- Условная вероятность
- Многомерные случайные величины
- Предельные теоремы теории вероятностей
- Оценки неизвестных параметров
- Генеральная совокупность

