Сечения тор с плоскостями частного положения
Тор является поверхностью вращения 4-го порядка (образующая и направляющая окружности 2-го порядка — порядки умножаются) и кривые ею сечений также являются кривыми 4-ю порядка (кроме круговых сечений).
Тор имеет две системы круговых сечений:
- первая система парных круговых сечений получается во всех плоскостях, проходящих через ось
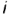 гора на той ею проекции, на которую ось
гора на той ею проекции, на которую ось 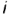 проецируется в точку, — смотри сечение во фронтально-проецирующей плоскости a(av) на фронтальной проекции тора (сечение по образующим окружностям
проецируется в точку, — смотри сечение во фронтально-проецирующей плоскости a(av) на фронтальной проекции тора (сечение по образующим окружностям 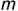 );
); - вторая система круговых сечений получается в плоскостях
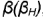 , перпендикулярных оси тора смотри сечение во фронтальной плоскости уровня на горизонтальной проекции тора (сечение по круговым параллелям гора).
, перпендикулярных оси тора смотри сечение во фронтальной плоскости уровня на горизонтальной проекции тора (сечение по круговым параллелям гора).
Тор имеет также третью систему сечений плоскостями уровня, параллельными оси его вращения  .
.
На рис. 4 85 показаны формы кривых в различных сечениях открытого тора плоскостями уровня (ось тора  ).
).
На рис. 4.85, а сечения проведены параллельно оси тора  на его фронтальной проекции и являются горизонтальными плоскостями уровня.
на его фронтальной проекции и являются горизонтальными плоскостями уровня.
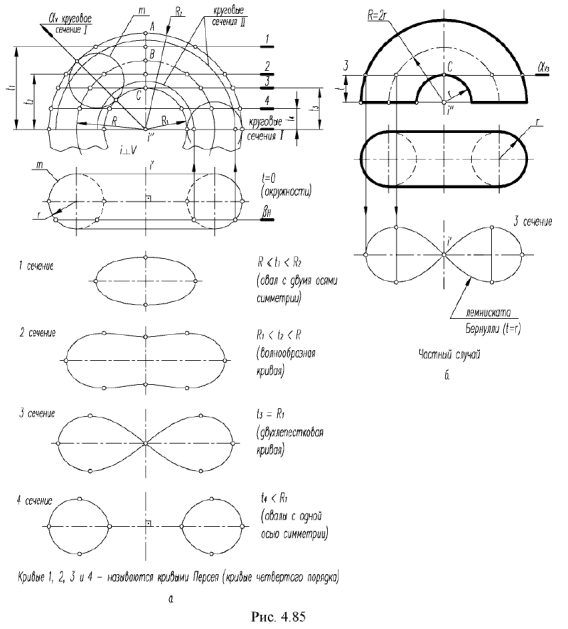
В зависимости от расстояния 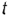 секущей плоскости до оси тора на его поверхности получается 4 вида кривых, объединенных общим названием кривые Персея (геометр Древней Греции):
секущей плоскости до оси тора на его поверхности получается 4 вида кривых, объединенных общим названием кривые Персея (геометр Древней Греции):
1-е сенате. Плоскость сечения на расстоянии 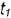 от оси тора образует на его поверхности кривую линию — овал с двумя осями симметрии (для плоскостей между точками
от оси тора образует на его поверхности кривую линию — овал с двумя осями симметрии (для плоскостей между точками 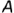 и
и 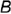 , т.е.
, т.е. 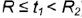 ).
).
2-е сечение. Плоскость сечения на расстоянии 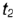 от оси тора образует на его поверхности волнообразную кривую (для плоскостей между точками
от оси тора образует на его поверхности волнообразную кривую (для плоскостей между точками 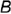 и
и 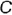 , т.е.
, т.е. 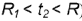 ).
).
3-е сечение. Плоскость сечения на расстоянии 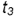 от оси тора образует на его поверхности двух лепестковую кривую (для плоскости, проходящей через точку
от оси тора образует на его поверхности двух лепестковую кривую (для плоскости, проходящей через точку 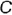 . т.е.
. т.е. 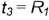 ).
).
4-е сечение.. Плоскость сечения на расстоянии 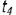 от оси тора образует на его поверхности два овала с одной осью симметрии (для плоскостей ниже точки
от оси тора образует на его поверхности два овала с одной осью симметрии (для плоскостей ниже точки 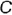 и не проходящих через ось вращения тора
и не проходящих через ось вращения тора 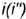 , т.е. когда
, т.е. когда 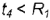 ).
).
На рис. 4.85. в изображена фронтальная и горизонтальная проекции открытого тора, у которого 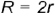 (частный случай). Кривые сечений этого тора называют овалами Кассини , а двухлепестковая кривая в сечении 3 называется лемнискатой Бернулли.
(частный случай). Кривые сечений этого тора называют овалами Кассини , а двухлепестковая кривая в сечении 3 называется лемнискатой Бернулли.
Построение проекции открытого тора со срезами плоскостями частного положения
На рис. 4.86 показан пример построения проекций отрытого тора с комбинированным срезом фронтально-проецирующей плоскостью 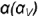 и горизонтальной плоскостью
и горизонтальной плоскостью 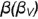
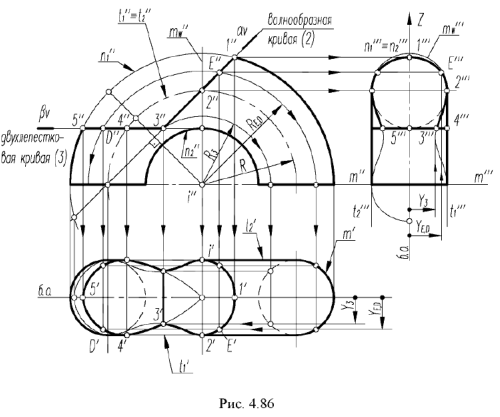
Для построения проекций тора со срезами следует выполнить предлагаемый графический алгоритм, определяющий порядок действий при решении всех подобных задач:
1-е действие. По заданным размерам построить на чертеже тонкими линиями фронтальную, горизонтальную и профильную проекции тора без срезов, а затем выполнить на его фронтальной проекции (или любой другой) заданные по условию срезы фронтально-проецирующей плоскостью 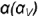 и горизонтальной плоскостью
и горизонтальной плоскостью 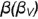 .
.
2-е действие. Обозначить на фронтальной проекции характерные точки и выполнить графо-аналитический анализ сечений:
Фронтально-проецирующая плоскость 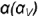 пересекает поверхность тора по участку волнообразной кривой 1-2-3 (сечение 2), часть которой ограничена вырожденной в точку фронтально-проецирующей линией пересечения 3-3 плоскостей среза
пересекает поверхность тора по участку волнообразной кривой 1-2-3 (сечение 2), часть которой ограничена вырожденной в точку фронтально-проецирующей линией пересечения 3-3 плоскостей среза 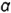 и
и 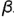 .
.
- Горизонтальная плоскость
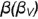 пересекает поверхность тора по участку двухлепестковой кривой 3-4-5 (сечение 3).
пересекает поверхность тора по участку двухлепестковой кривой 3-4-5 (сечение 3).
!!! Поскольку горизонтальная проекция тора имеет вертикальную симметрию, точки обозначены на одной его половине (нижней).
3-е действие. Достроить горизонтальную проекцию гора, построив проекции плоскостей срезов по горизонтальным проекциям отмеченных точек, и определить видимость плоскостей срезов;
- Горизонтальная проекция видимого участка волнообразной кривой в плоскости а построена по проекциям обозначенных точек
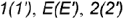 и
и 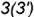 по их принадлежности характерным
по их принадлежности характерным 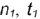 и
и 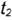 (точки 1 и 2) и вспомогательным (точки
(точки 1 и 2) и вспомогательным (точки 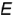 и 3) параллелям.
и 3) параллелям. - Горизонтальная проекция видимого участка двухлепестковой кривой в плоскости
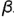 построена по проекциям обозначенных точек
построена по проекциям обозначенных точек 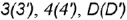 и
и 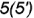 по их принадлежности характерным
по их принадлежности характерным 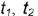 и
и 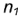 (точки 4 и 5) и вспомогательным (точки
(точки 4 и 5) и вспомогательным (точки 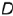 ) параллелям (точки
) параллелям (точки 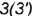 уже построены).
уже построены). - Видимый отрезок
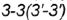 — горизонтальная проекция линии пересечения плоскостей срезов
— горизонтальная проекция линии пересечения плоскостей срезов 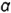 и
и 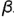 . ограничивающая участки кривых в плоскостях срезов.
. ограничивающая участки кривых в плоскостях срезов.
4-е действие. Выполнить графический анализ построенной горизонтальной проекции тора для определения ее очерка и внутреннего контура:
У. Горизонтальный очерк определяют:
- видимые половины окружностей
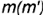 ,
, - участки очерковых параллелей
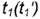 и
и 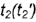 , не существующие между точками
, не существующие между точками 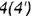 и
и 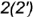
-участки кривых 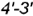 и
и 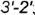
- Внутренний кон гур определяют:
- невидимые половины окружностей
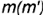 .
. - видимые участки кривых
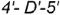 и
и 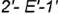
- видимый отрезок
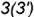 пересечения плоскостей срезов
пересечения плоскостей срезов 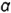 и
и 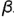 .
.
5-е действие. Достроить профильную проекцию тора, построив проекции плоскостей срезов по профильным проекциям обозначенных точек, и определить видимость плоскостей срезов:
- Профильная проекция видимого участка волнообразной кривой построена по проекциям обозначенных точек
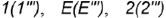 и
и 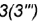 по их принадлежности характерным параллелям
по их принадлежности характерным параллелям 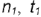 и
и 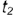 (точки
(точки  и
и  ) и по координатам
) и по координатам 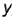 (точки
(точки 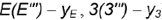 ).
). - Профильная проекция горизонтальной плоскости среза
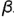 проецируется в видимый горизонтальный отрезок
проецируется в видимый горизонтальный отрезок 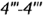 (точки
(точки 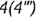 на очерковых линиях
на очерковых линиях 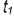 и
и 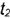 ).
).
6-е действие. Выполнить графический анализ построенной профильной проекции тора для определения ее очерка и внутреннего контура:
6.1 Профильный очерк определяют
- слева и справа проекции очерковых параллелей
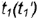 и
и 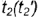 до точек
до точек 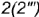
- сверху — видимый участок
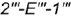 волнообразной кривой;
волнообразной кривой; - снизу — видимые совпадающие проекции образующих окружностей
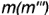
- Внутренний контур определяют:
- видимый горизонтальный отрезок
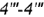 (проекция плоскости среза
(проекция плоскости среза 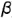 );
);
-видимые участки 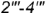 волнообразной кривой;
волнообразной кривой;
- невидимая часть окружности
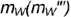 между точками
между точками 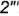 .
.
7-е действие. Оформить чертеж гора, выполнив толстыми сплошными линиями очерки и видимый внутренний контур каждой проекций (оставить тонкими линиями полные очерки проекций и линии построений).
Эта теория взята со страницы задач по начертательной геометрии:
Возможно эти страницы вам будут полезны:
| Построение проекции открытого тора |
| Построение проекции точек, лежащих на поверхности тора |
| Метод проекции и свойства |
| Точка в системе плоскостей проекций h v и w |
