Оглавление:
Последовательность считается заданной, если известен закон, по которому можно вычислить любой ее член 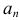 при данном
при данном 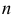 .
.
Определение 1. Числовым рядом называется выражение
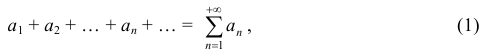
где числа  , называемые членами ряда, образуют числовую последовательность.
, называемые членами ряда, образуют числовую последовательность.
Определение 2. Суммой конечного числа 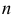 первых членов ряда называется
первых членов ряда называется 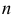 -й частичной суммой ряда:
-й частичной суммой ряда: 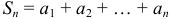 .
.
Определение 3. Числовой ряд (1) называется сходящимся, если существует конечный предел 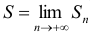 . Этот предел называется суммой сходящегося ряда. Если предел не существует, то ряд (1) называется расходящимся.
. Этот предел называется суммой сходящегося ряда. Если предел не существует, то ряд (1) называется расходящимся.
Свойства сходящихся рядов
1. На сходимость ряда не влияет отбрасывание конечного числа его членов.
2. Если ряд (1) сходится и его сумма равна 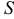 , то ряд
, то ряд  , где
, где 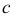 — любое число, также сходится и его сумма равна
— любое число, также сходится и его сумма равна 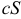 .
.
3. Если ряды (1) и  сходятся и их суммы равны
сходятся и их суммы равны 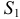 и
и 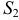 , то ряды
, то ряды 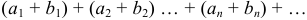 и
и 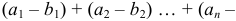
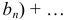 также сходятся и их суммы соответственно равны
также сходятся и их суммы соответственно равны 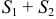 и
и  .
.
Признаки сходимости числовых рядов
Необходимый признак сходимости. Ряд может сходиться лишь при условии, когда общий член ряда 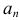 при
при 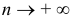 стремится к нулю:
стремится к нулю: 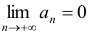 .
.
Следствие. Если общий член ряда 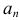 при
при 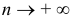 не стремится к нулю, то ряд расходится.
не стремится к нулю, то ряд расходится.
Признак Д’ Аламбера. Если в ряде (1) с положительными членами отношение 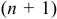 -го члена к
-го члена к 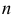 -му при
-му при 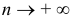 имеет предел
имеет предел 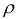 , т.е.
, т.е. 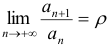 , то при
, то при 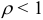 ряд сходится, при
ряд сходится, при 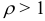 или
или 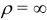 ряд расходится. При
ряд расходится. При 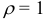 вопрос о сходимости ряда решается с использованием других признаков.
вопрос о сходимости ряда решается с использованием других признаков.
Например, если 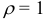 , но отношение
, но отношение 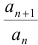 для всех номеров
для всех номеров 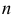 , начиная с некоторого, больше единицы, то ряд расходится.
, начиная с некоторого, больше единицы, то ряд расходится.
Признак сравнения рядов
Если ряд с положительными членами 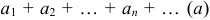 сравнить с другим рядом с положительными членами
сравнить с другим рядом с положительными членами 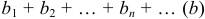 сходимость или расходимость которого известна, и если начиная с некоторого номера
сходимость или расходимость которого известна, и если начиная с некоторого номера 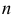 : 1)
: 1) 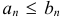 и ряд
и ряд 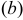 сходится, то и ряд
сходится, то и ряд 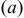 также сходится; 2)
также сходится; 2) 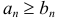 и ряд
и ряд 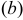 расходится, то и ряд
расходится, то и ряд 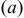 также расходится.
также расходится.
Предельный признак сравнения рядов
Если существует конечный предел неравный нулю 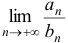 , то ряд
, то ряд 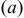 и ряд
и ряд  ведут себя одинаково, т. е. либо оба сходятся, либо расходятся.
ведут себя одинаково, т. е. либо оба сходятся, либо расходятся.
При использовании признака сравнения исследуемый ряд  часто сравнивают или с бесконечной геометрической прогрессией
часто сравнивают или с бесконечной геометрической прогрессией 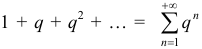 , которая при
, которая при 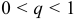 сходится, при
сходится, при 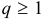 расходится; или с расходящимся гармоническим рядом
расходится; или с расходящимся гармоническим рядом 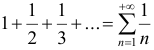 ; или с рядом
; или с рядом 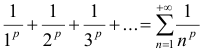 , который сходится при
, который сходится при 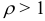 и расходится при
и расходится при 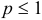 .
.
Ряды вида 
где 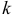 — степень многочлена
— степень многочлена 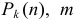 — степень многочлена
— степень многочлена 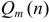 , что следует из предельного признака сравнения с рядом
, что следует из предельного признака сравнения с рядом 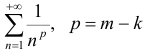 .
.
Радикальный признак Коши
Если для ряда с положительными членами 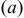 величина
величина 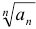 имеет конечный предел
имеет конечный предел 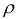 при
при 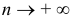 , т. е.
, т. е. 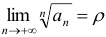 , то при
, то при 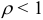 ряд сходится; при
ряд сходится; при 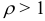 ряд расходится. При
ряд расходится. При 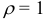 вопрос о сходимости ряда решается с использованием других признаков.
вопрос о сходимости ряда решается с использованием других признаков.
Радикальный признак Коши обычно применяется, когда общий член ряда 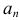 содержит показательно — степенную функцию вида
содержит показательно — степенную функцию вида 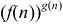 .
.
Интегральный признак Коши. Ряд с положительными убывающими членами 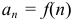 сходится или расходится, смотря по тому, сходится или расходится несобственный интеграл
сходится или расходится, смотря по тому, сходится или расходится несобственный интеграл 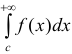 , где
, где 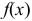 — непрерывная убывающая функция;
— непрерывная убывающая функция; 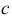 — любое положительное число из области определения
— любое положительное число из области определения 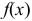 .
.
Этим признаком можно пользоваться, когда выражение общего члена  имеет смысл не только для целых положительных значений
имеет смысл не только для целых положительных значений  . Эффективность признака зависит от сложности вычисления несобственного интеграла.
. Эффективность признака зависит от сложности вычисления несобственного интеграла.
Пример №1
Исследовать сходимость числового ряда 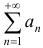 .
.
Решение:
1) 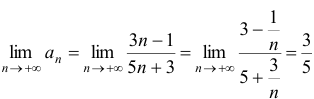 . Необходимый признак сходимости не выполняется. Поэтому этот ряд расходится.
. Необходимый признак сходимости не выполняется. Поэтому этот ряд расходится.
2) Общий член ряда содержит факториал. Поэтому воспользуемся признаком Д’ Аламбера. Найдем 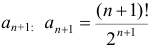 .
.
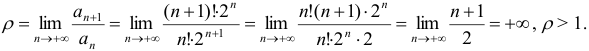 Согласно признаку Д’ Аламбера данный ряд расходится.
Согласно признаку Д’ Аламбера данный ряд расходится.
3) Общий член ряда есть дробь, в числителе находится степенная функция, а в знаменателе показательная функция. Поэтому воспользуемся признаком Д’ Аламбера. Найдем 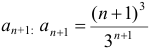 .
.
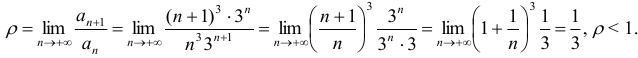
Согласно признаку Д’ Аламбера данный ряд сходится.
4) Каждый член 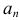 данного ряда меньше соответствующего члена
данного ряда меньше соответствующего члена 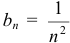 сходящегося ряда. Поэтому, согласно признаку сравнения, данный ряд сходится.
сходящегося ряда. Поэтому, согласно признаку сравнения, данный ряд сходится.
5) Несобственный интеграл от непрерывной и убывающей функции 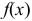 с бесконечным верхним пределом вычислить несложно. Поэтому воспользуемся интегральным признаком Коши при условии, что нижний предел равен двум или любому другому числу большему единице.
с бесконечным верхним пределом вычислить несложно. Поэтому воспользуемся интегральным признаком Коши при условии, что нижний предел равен двум или любому другому числу большему единице.
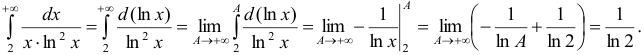
Несобственный интеграл сходится. Поэтому согласно интегральному признаку Коши данный ряд сходится.
6) Общий член ряда содержит показательно — степенную функцию. Поэтому применим радикальный признак Коши:
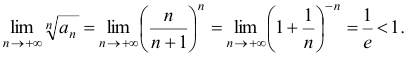 Согласно радикальному признаку Коши ряд сходится.
Согласно радикальному признаку Коши ряд сходится.
Определение 4. Знакочередующимся числовым рядом (знаки членов которого строго чередуются) называется ряд вида
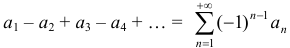 , где числа
, где числа 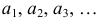 положительны. (2)
положительны. (2)
Признак Лейбница
Если в знакочередующемся ряде (2) члены таковы, что 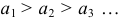 и
и 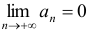 , то ряд (2) сходится, его сумма положительна и не превосходит первого члена.
, то ряд (2) сходится, его сумма положительна и не превосходит первого члена.
Признак Лейбница справедлив, если неравенства выполняются, начиная с некоторого номера 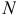 .
.
Ошибка при замене суммы ряда, удовлетворяющего признаку Лейбница, суммой нескольких его первых членов меньше абсолютного значения первого из отброшенных членов.
Определение 5. Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные.
Определение 6. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных значений его членов.
Определение 7. Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится, то данный знакопеременный ряд называется условно или не абсолютно сходящимся рядом.
Свойства абсолютно и условно сходящихся рядов
- Если ряд сходится абсолютно, то он остается абсолютно сходящимся при любой перестановке его членов. При этом сумма ряда не зависит от порядка его членов.
- Если ряд сходится условно, то, какое бы мы ни задали число
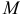 , можно так переставить члены этого ряда, чтобы его сумма оказалась в точности равной
, можно так переставить члены этого ряда, чтобы его сумма оказалась в точности равной 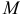 . Более того, можно так переставить члены условно сходящегося ряда, чтобы ряд, полученный после перестановки, оказался расходящимся.
. Более того, можно так переставить члены условно сходящегося ряда, чтобы ряд, полученный после перестановки, оказался расходящимся.
Определение 8. Функциональным рядом называется выражение
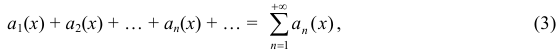
члены которого являются функциями от переменной 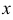 .
.
При различных значениях 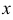 из функционального ряда получаются различные числовые ряды, которые могут быть сходящимися или расходящимися. Совокупность значений
из функционального ряда получаются различные числовые ряды, которые могут быть сходящимися или расходящимися. Совокупность значений 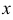 , при которых функциональный ряд сходится, называется его областью сходимости. Суммой функционального ряда называется функция
, при которых функциональный ряд сходится, называется его областью сходимости. Суммой функционального ряда называется функция 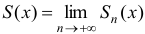 , а разность
, а разность 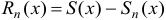 — остатком ряда.
— остатком ряда.
Определение 9. Ряд (3) называется равномерно сходящимся на отрезке 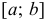 , если для любого
, если для любого 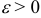 найдется такой номер
найдется такой номер 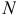 , что при
, что при 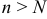 и любом
и любом 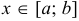 будет выполнено неравенство
будет выполнено неравенство 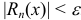 .
.
Для определения области сходимости функциональных рядов обычно вначале используется признак Д’ Аламбера, а затем те значения 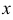 , для которых этот признак не решает вопроса о сходимости ряда, исследуются особо, посредством других признаков сходимости рядов.
, для которых этот признак не решает вопроса о сходимости ряда, исследуются особо, посредством других признаков сходимости рядов.
Определение 10. Степенным рядом называется функциональный ряд
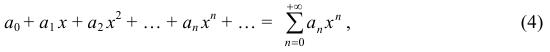
где 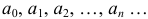 — постоянные числа, называемые коэффициентами ряда.
— постоянные числа, называемые коэффициентами ряда.
Определение 11. Интервалом сходимости степенного ряда называется такой интервал от 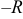 до
до 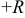 , что для всякой точки
, что для всякой точки 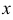 , лежащей внутри этого интервала, ряд сходится и притом абсолютно, а для точек
, лежащей внутри этого интервала, ряд сходится и притом абсолютно, а для точек 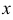 , лежащих вне его, ряд расходится. Число
, лежащих вне его, ряд расходится. Число 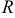 называется радиусом сходимости степенного ряда.
называется радиусом сходимости степенного ряда.
Радиус сходимости 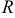 степенного ряда можно определить по признаку Д’ Аламбера
степенного ряда можно определить по признаку Д’ Аламбера
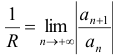 , или по признаку Коши
, или по признаку Коши 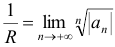 .
.
Теорема Абеля
1) Если степенной ряд сходится при некотором значении 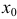 , не равном нулю, то он абсолютно сходится при всяком значении
, не равном нулю, то он абсолютно сходится при всяком значении 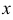 , для которого
, для которого 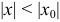 ;
;
2) если ряд расходится при некотором значении 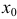 , то он расходится при всяком
, то он расходится при всяком 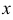 , для которого
, для которого 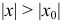 .
.
Степенной ряд в своем интервале сходимости по отношению к операциям дифференцирования и интегрирования ведет себя так же, как многочлен с конечным число членов.
Определение 12. Рядом Тейлора для функции 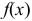 в окрестности точки
в окрестности точки 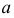 называется степенной ряд относительно двучлена
называется степенной ряд относительно двучлена 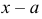
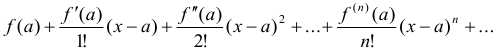
При 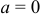 ряд Тейлора есть степенной ряд относительно независимой переменной
ряд Тейлора есть степенной ряд относительно независимой переменной 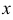 , называемый рядом Маклорена:
, называемый рядом Маклорена:
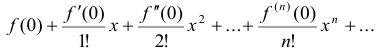
Примеры разложения функции в ряды
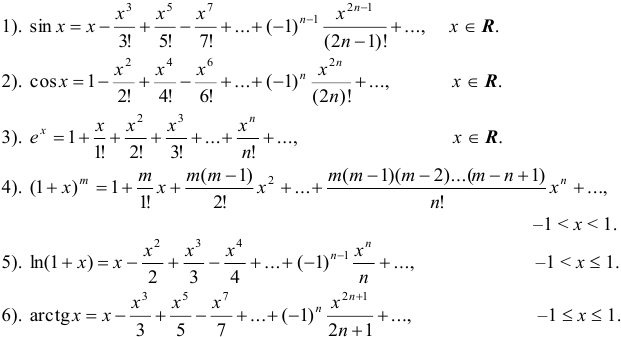
Пример №2
Найти область сходимости степенного ряда 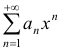 .
.

Решение:
1) Найдем радиус сходимости  степенного ряда:
степенного ряда:
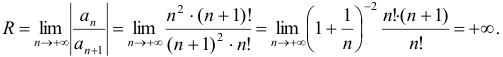
Следовательно, 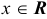 .
.
2) Найдем радиус сходимости 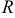 степенного ряда:
степенного ряда:
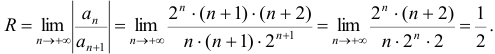
Радиус сходимости 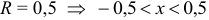 .
.
Согласно признаку Д’ Аламбера при любых значениях 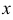 из найденного интервала ряд абсолютно сходится, а при
из найденного интервала ряд абсолютно сходится, а при 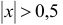 расходится. Граничные точки
расходится. Граничные точки 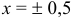 исследуем особо.
исследуем особо.
При  получим числовой знакочередующийся ряд
получим числовой знакочередующийся ряд 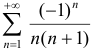 , который сходится согласно признаку Лейбница (члены этого ряда убывают по абсолютному значению, стремясь к нулю).
, который сходится согласно признаку Лейбница (члены этого ряда убывают по абсолютному значению, стремясь к нулю).
При 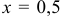 получим числовой ряд с положительными членами
получим числовой ряд с положительными членами 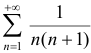 , который сходится, что следует из сравнения его с сходящимся рядом
, который сходится, что следует из сравнения его с сходящимся рядом 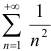 (каждый член исследуемого ряда меньше соответствующего члена сравниваемого ряда).
(каждый член исследуемого ряда меньше соответствующего члена сравниваемого ряда).
Следовательно, интервал сходимости ряда является отрезок 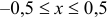 .
.
Пример №3
Вычислить определенный интеграл 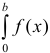 с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.
с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.

Решение:
1) Пользуясь рядом Маклорена для 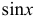 , заменяя в нем
, заменяя в нем 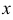 на
на 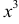 , имеем
, имеем 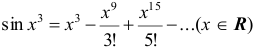 . Интегрируя в пределах от 0 до 1, получим
. Интегрируя в пределах от 0 до 1, получим
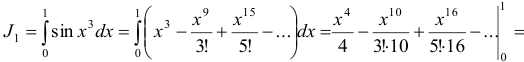
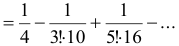
Третий член этого знакочередующегося ряда меньше 0,001. Поэтому для вычисления искомого приближенного значения интеграла достаточно взять сумму двух первых членов ряда: 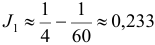 .
.
2) Пользуясь рядом Маклорена для 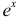 , заменяя в нем
, заменяя в нем 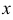 на
на 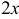 , имеем
, имеем 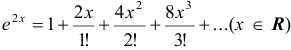 . Умножая полученный ряд на
. Умножая полученный ряд на 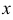 , и интегрируя в пределах от 0 до 0,25, получим
, и интегрируя в пределах от 0 до 0,25, получим
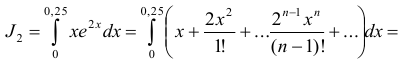
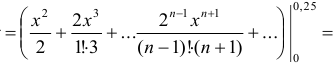
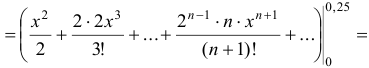
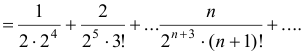
Исследуем сходимость полученного числового ряда по признаку Д’ Аламбера
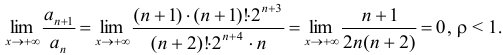
Согласно признаку Д’ Аламбера полученный числовой ряд сходится, причем абсолютно. Поэтому представим 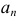 — ый член в виде
— ый член в виде 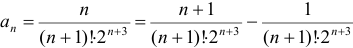 .
.
Тогда 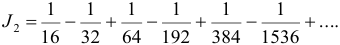
Шестой член этого знакочередующегося ряда меньше 0,001. Поэтому для вычисления искомого приближенного значения интеграла достаточно взять сумму пяти первых членов ряда: 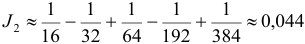 .
.
Пример №4
Найти три первых, отличных от нуля члена разложения в степенной ряд решения 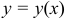 дифференциального уравнения
дифференциального уравнения 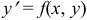 , удовлетворяющего начальному условию
, удовлетворяющего начальному условию 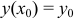 .
.

Решение:
1) Пусть искомая функция 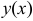 разложена в ряд Маклорена
разложена в ряд Маклорена 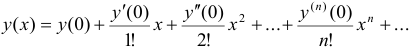 , где
, где 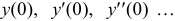 являются значениями функции
являются значениями функции 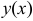 и ее производных при
и ее производных при 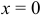 .
.
Согласно начальному условию первый коэффициент 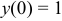 . Второй получим при подстановке известных величин в данное уравнение,
. Второй получим при подстановке известных величин в данное уравнение, 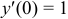 . Третий коэффициент найдем путем дифференцирования данного уравнения:
. Третий коэффициент найдем путем дифференцирования данного уравнения: 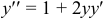 . Отсюда при
. Отсюда при 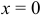 получим:
получим: 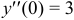 .
.
Подставляя эти значения коэффициентов в ряд Маклорена, получим 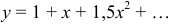
2) Применяя тот же способ, что и в решении предыдущей задачи, получим:
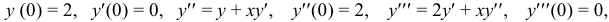
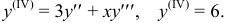
Подставляя эти значения коэффициентов в ряд Маклорена, получим
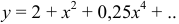
Примечание. Если 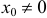 , то искомую функцию
, то искомую функцию 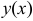 ищем в виде разложения в ряд Тейлора по степеням
ищем в виде разложения в ряд Тейлора по степеням 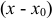 .
.
Определение 13. Функциональный ряд вида
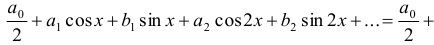
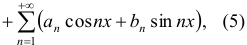
называется тригонометрическим рядом. Постоянные числа 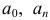 и
и 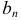
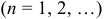 называются коэффициентами тригонометрического ряда.
называются коэффициентами тригонометрического ряда.
Если ряд (5) сходится, то его сумма есть периодическая функция 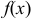 с периодом
с периодом 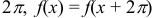 .
.
Определение 14. Рядом Фурье для функции 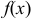 в интервале от
в интервале от 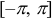 называется тригонометрический ряд (5), если его коэффициенты
называется тригонометрический ряд (5), если его коэффициенты 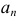 и
и 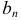 вычислены по формулам Фурье:
вычислены по формулам Фурье:
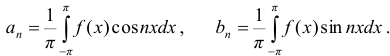
Теорема Дирихле (достаточные условия разложимости функции в ряд Фурье). Если в интервале 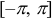 функция
функция 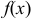 кусочно монотонная и ограниченная, то ее ряд Фурье сходится во всех точках этого интервала, т.е. имеет сумму
кусочно монотонная и ограниченная, то ее ряд Фурье сходится во всех точках этого интервала, т.е. имеет сумму 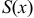 . При этом: 1) в точках непрерывности функции
. При этом: 1) в точках непрерывности функции 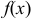 он сходится к самой функции,
он сходится к самой функции, 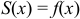 ; 2) в каждой точке разрыва
; 2) в каждой точке разрыва 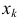 функции — к полусумме односторонних пределов функции слева и справа,
функции — к полусумме односторонних пределов функции слева и справа, 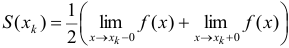 ; 3) в обоих граничных точках интервала
; 3) в обоих граничных точках интервала 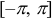 — к полусумме односторонних пределов функции при стремлении
— к полусумме односторонних пределов функции при стремлении 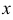 к этим точкам изнутри интервалов,
к этим точкам изнутри интервалов, 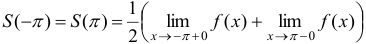 .
.
Для четной функции 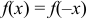 ряд Фурье не содержит синусов
ряд Фурье не содержит синусов
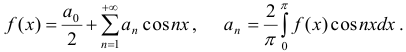
Для нечетной функции 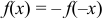 ряд Фурье содержит только синусы
ряд Фурье содержит только синусы
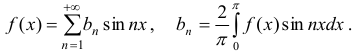
Для периодической функции 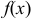 с периодом
с периодом 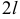 в интервале
в интервале 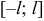 ряд Фурье имеет вид
ряд Фурье имеет вид
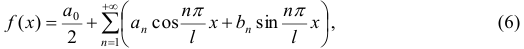
где
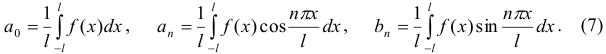
При разложении функции 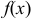 в ряд Фурье в интервале
в ряд Фурье в интервале 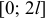 пределы интегралов в формулах (7) будут 0 и
пределы интегралов в формулах (7) будут 0 и 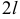 , а в случае произвольного интервала
, а в случае произвольного интервала 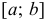 длины
длины 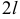 эти пределы будут
эти пределы будут 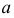 и
и 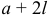 .
.
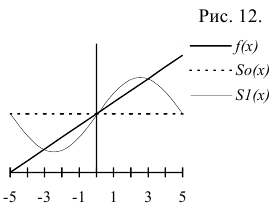
Пример №5
Разложить данную функцию 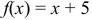 в ряд Фурье в интервале (-5; 5). Построить графики функции
в ряд Фурье в интервале (-5; 5). Построить графики функции 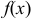 и частичных сумм
и частичных сумм 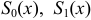 ряда Фурье в указанном интервале.
ряда Фурье в указанном интервале.
Решение:
Данная функция является ни четной и ни нечетной, поэтому вычислим ее коэффициенты Фурье по общим формулам (6) и (7):
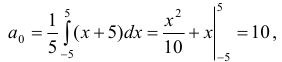
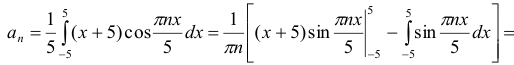
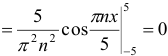
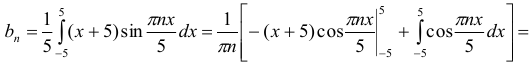
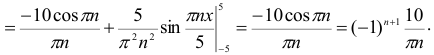
При вычислении интеграла применена формула интегрирования по частям. Искомое разложение данной функции в ряд Фурье в интервале (-5; 5) имеет вид
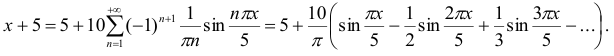
На рис. 12 показаны графики функций 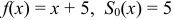 и
и 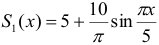 в интервале (-5; 5).
в интервале (-5; 5).
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Криволинейный интеграл |
| Векторный анализ: основные понятия и пример с решением |
| Определители матрицы: алгоритм, примеры вычисления |
| Матрицы. Операции над матрицами |

