Резонанс напряжений
Если в цепи синусоидального тока с последовательно соединенными конденсатором ёмкостью 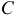 и катушкой с сопротивлением
и катушкой с сопротивлением 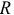 и индуктивностью
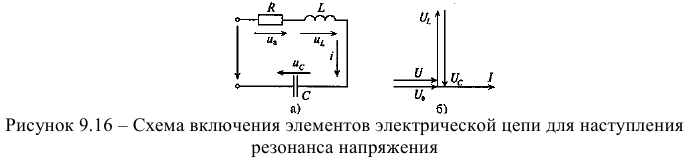
и индуктивностью 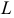 (рис. 9.16 а) равны реактивные сопротивления, то в цепи наступает резонанс напряжений. Равенство реактивных сопротивлений является условием резонанса напряжений.
(рис. 9.16 а) равны реактивные сопротивления, то в цепи наступает резонанс напряжений. Равенство реактивных сопротивлений является условием резонанса напряжений.
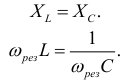
тогда частота резонанса определяется выражением
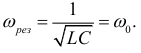
Резонанс напряжений имеет место в неразветвленной цепи с 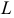 и
и 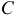 тогда, когда частота вынужденных колебаний (частота источника)
тогда, когда частота вынужденных колебаний (частота источника) 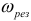 , будет равна частоте собственных колебаний резонансного контура
, будет равна частоте собственных колебаний резонансного контура 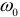 .
.
Следовательно, добиться резонанса напряжений можно изменением частоты источника 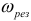 или изменением параметров колебательного контура
или изменением параметров колебательного контура 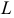 или
или 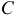 , т.е. изменением частоты собственных колебаний
, т.е. изменением частоты собственных колебаний 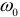 .
.
Полное сопротивление цепи (рис. 9.16 а) при резонансе напряжений определяется по формуле: 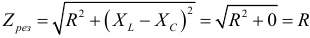 , так как,
, так как, 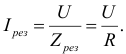 .
.
Ток в неразветвленной цепи при резонансе напряжений максимальный:
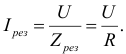
Реактивные сопротивления при резонансе напряжений равны между собой, т. е.
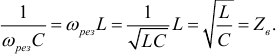
Таким образом, реактивные сопротивления при резонансе напряжений равны (каждое) волновому сопротивлению 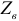 , которое называют характеристическим сопротивлением:
, которое называют характеристическим сопротивлением:
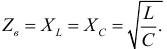
Напряжения на индуктивности 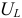 и на емкости
и на емкости 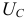 при резонансе напряжений равны между собой, так как равны сопротивления.
при резонансе напряжений равны между собой, так как равны сопротивления.
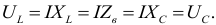
Данное равенство определяет название «резонанс напряжений» Так как 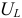 и
и 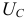 изменяются в противофазе, то напряжение в резонансном режиме равно напряжению на активном сопротивлении
изменяются в противофазе, то напряжение в резонансном режиме равно напряжению на активном сопротивлении 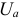 , т. е.
, т. е. 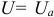 , что видно на векторной диаграмме (рис. 9.16 б).
, что видно на векторной диаграмме (рис. 9.16 б).
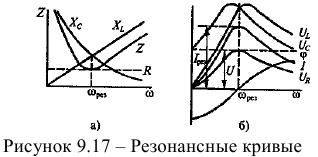
На резонансных кривые чётко просматриваются значения этих параметров при частоте резонанса 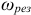 (рис. 9.17).
(рис. 9.17).
Резонанс токов в цепи параллельным включением катушки и конденсатора (в различных ветвях) возникает при равенстве реактивных проводимостей в ветвях: 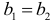 или
или 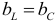 .
.
Данное выражение является условием резонанса током в разветвленных цепях синусоидального тока.
Полная проводимость при этом условии
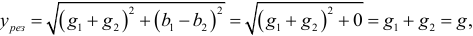
так как 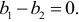
Ток в неразветвленной части цепи при резонансе токов имеет минимальную величину: 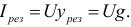
Реактивные токи в ветвях при резонансе токов равны между собой
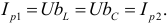
Это равенство и определяет название «резонанс токов».
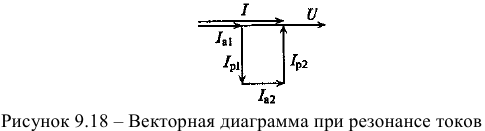
Векторная диаграмма при резонансе токов (рис. 9.18). Реактивные токи находятся в противофазе, поэтому ток в неразветвленной части цепи 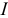 при резонансе токов равен активному току
при резонансе токов равен активному току 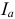 , и совпадает по фазе с напряжением, т. е.
, и совпадает по фазе с напряжением, т. е. 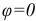 , a
, a 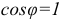 . Следовательно, вся мощность цепи
. Следовательно, вся мощность цепи 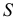 при резонансе токов является активной
при резонансе токов является активной 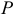 :
: 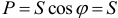 .
.
Частота при резонансе токов определяется:
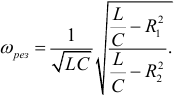
Эта страница взята со страницы лекций по предмету теоретические основы электротехники (ТОЭ):
Предмет теоретические основы электротехники
Возможно эти страницы вам будут полезны:

