Оглавление:
Прежде чем изучать готовые решения по экономико математическим методам, нужно знать теорию, поэтому для вас я подготовила краткую теорию по предмету «Экономико математические методы» и решения с примерами.
Эта страница подготовлена для студентов.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Экономико-математические методы
Термин экономико-математические методы понимается как обобщающее название комплекса экономических и математических научных дисциплин, объединенных для изучения социально-экономических систем и процессов. Под социально-экономической системой будем понимать сложную вероятностную динамическую систему, охватывающую процессы производства, обмена, распределения и потребления материальных и других благ.
Основным методом исследования систем и процессов является метод моделирования, т. е. способ теоретического анализа и практического действия, направленный на разработку и использование моделей. При этом под моделью будем понимать образ реального объекта (процесса) в материальной или идеальной форме (т. е. описанный знаковыми средствами на каком-либо языке), отражающий существенные свойства моделируемого объекта (процесса) и замещающий его в ходе исследования и управления. В дальнейшем мы будем говорить только об экономикоматематическом моделировании, т. е. об описании знаковыми математическими средствами социально-экономических систем.
Практическими задачами экономико математического моделирования являются:
- анализ экономических объектов и процессов;
- прогнозирование развития экономических процессов;
- выработка управленческих решений на всех yровнях хозяйственной иерархии.
Постановка задачи линейного программирования
Задача линейного программирования (ЛП) в общем виде записывается следующим образом (1.1)—(1.4). Каждой задаче ЛП может быть поставлена в соответствие другая вполне определенная задача ЛП, такая, что при решении одной из них одновременно решается и другая. Эти задачи названы парой взаимодвойственных задач. Любой задаче ЛП (1.1)—(1.4) можно поставить в соответствие двойственную задачу вида (1.5)—(1.8):
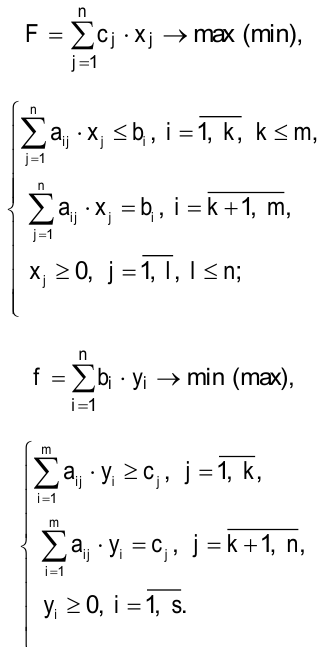
где 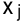 — неизвестные величины;
— неизвестные величины;
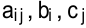 — заданные действительные числа;
— заданные действительные числа;
(1.1), (1.5) — целевые функции (ЦФ);
(1.2), (1.3), (1.6), (1.7) — основные ограничения задачи;
(1.4) — не основные ограничения;
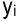 имеет произвольный знак для
имеет произвольный знак для 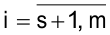 .
.
Для решения задач ЛП может быть использован графический метод, симплекс-метод, метод искусственного базиса, модифицированный симплекс-метод и двойственный симплекс-метод.
Правила составления двойственных задач:
1) число неизвестных одной задачи равно числу ограничений второй;
2) матрицы коэффициентов системы ограничений получаются одна из другой путем транспонирования;
3) знаки неравенств в системе ограничений заменяют на противоположные, например, < на >, и наоборот;
4) свободные члены ограничений исходной задачи становятся коэффициентами целевой функции двойственной задачи и, наоборот, коэффициенты целевой функции исходной задачи преобразуются в свободные члены ограничений двойственной;
5) критерий оптимальности целевой функции заменяется на противоположный, например, max на min.
Возможно эта страница вам будет полезна:
| Предмет экономико-математические методы (ЭММ) |
Анализ линейных моделей на чувствительность (устойчивость)
Анализ линейных моделей на чувствительность — это процесс, реализуемый после нахождения оптимального решения. При таком анализе рассматривается комплекс линейных оптимизационных моделей. Это придаст задаче определенную динамичность, что позволяет проанализировать влияние возможных изменений исходных данных на полученное ранее оптимальное решение.
Неизбежное колебание значений таких экономических параметров, как цены на продукцию и сырье, запасы сырья, спрос на рынке и т. д., может привести к нсоптимальности или непригодности прежнего режима работы. Для учета подобных ситуаций проводится анализ чувствительности, т. е. анализ того, как возможные изменения параметров исходной модели повлияют на полученное ранее оптимальное решение задачи ЛП.
Отсутствие такого анализа может привести к тому, что полученное оптимальное решение устареет еще до своей реализации.
Основные задачи анализа на чувствительность’.
- Анализ изменения запасов ресурсов позволяет ответить на вопросы:
- на сколько можно увеличить запас некоторого дефицитного ресурса с целью улучшения значения целевой функции;
- на сколько можно уменьшить запас некоторого недефицитного ресурса с сохранением полученного ранее оптимального значения целевой функции.
Если ресурс израсходован полностью, его относят к разряду дефицитных. Ресурс в избытке называют недефицитным. Объем недефицитного ресурса можно уменьшить на величину избытка без изменения значения целевой функции. Объем дефицитного ресурса не следует увеличивать сверх того предела, когда соответствующее ему ограничение становится избыточным.
- Определение наиболее выгодного ресурса позволяет ответить на вопрос, какому из дефицитных ресурсов следует отдать предпочтение при вложении дополнительных средств. Вводится характеристика ценности единицы ресурса:
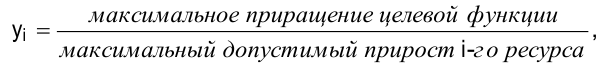
где 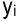 — теневая цена ресурса.
— теневая цена ресурса.
Теневая цена показывает, на сколько изменится значение целевой функции при изменении запаса ресурса на единицу.
Теневая цена позволяет определить статус ресурса. У недефицитного ресурса теневая цена равна нулю, положительное значение теневой цены говорит о дефицитности данного ресурса.
Значение теневой цены ресурсов — это решение задачи, двойственной к данной.
- Определение пределов изменения коэффициентов ЦФ позволяет ответить на вопросы:
- каков диапазон изменения того или иного коэффициента ЦФ, при котором не происходит изменение оптимального решения;
- на сколько следует изменить тот или иной коэффициент ЦФ, чтобы сделать дефицитный ресурс недефицитным, и наоборот.
Возможно эта страница вам будет полезна:
| Экономико-математические методы задачи с решением и примерами |
Экономическая интерпретация решения задач
Задача №1.1.
Предприятие изготавливает два вида продукции — 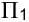 и
и 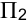 . Для производства продукции используется два вида сырья — А и Б. Максимально возможные запасы сырья, расход сырья на единицу приведены в таблице.
. Для производства продукции используется два вида сырья — А и Б. Максимально возможные запасы сырья, расход сырья на единицу приведены в таблице.

Опыт работы показал, что суточный спрос на продукцию 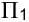 никогда не превышает спрос на продукцию
никогда не превышает спрос на продукцию 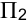 больше, чем на единицу. Спрос на продукцию
больше, чем на единицу. Спрос на продукцию 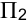 не превышает 2-х единиц в сутки. Цена реализации
не превышает 2-х единиц в сутки. Цена реализации 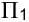 составляет 3 денежные единицы,
составляет 3 денежные единицы, 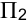 — 4 денежные единицы.
— 4 денежные единицы.
Какой объем продукции каждого вида должно выпускать предприятие, чтобы максимизировать свой суточный доход?
Решение:
Введем переменные: 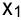 — объем выпуска продукции
— объем выпуска продукции 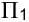 ;
; 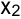 — объем выпуска продукции
— объем выпуска продукции 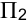 . Математическая модель задачи и задача в каноническом виде имеют следующий вид:
. Математическая модель задачи и задача в каноническом виде имеют следующий вид:
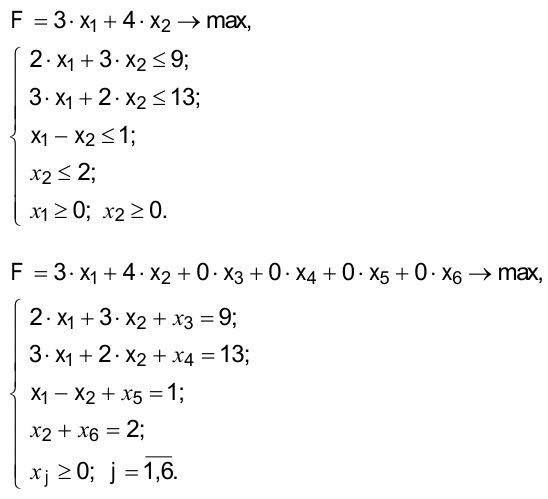
Дополнительные переменные (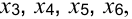 которые прибавили к левым частям соответствующих неравенств) имеют экономический смысл: они показывают величину неиспользованного ресурса. Так, в данном примере
которые прибавили к левым частям соответствующих неравенств) имеют экономический смысл: они показывают величину неиспользованного ресурса. Так, в данном примере 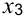 показывает величину неиспользованного сырья А,
показывает величину неиспользованного сырья А, 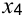 — сырья Б,
— сырья Б, 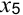 показывает неиспользованную разницу в спросе на продукцию
показывает неиспользованную разницу в спросе на продукцию 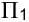 и
и 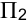 ,
, 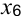 — невостребованное количество продукции
— невостребованное количество продукции  .
.
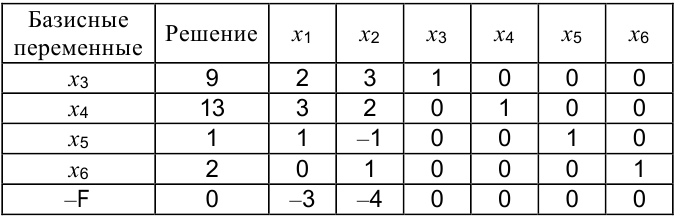
Составим исходную симплекс-таблицу:
Решая задачу симплекс-методом, получим следующую итоговую симплекс-таблицу:
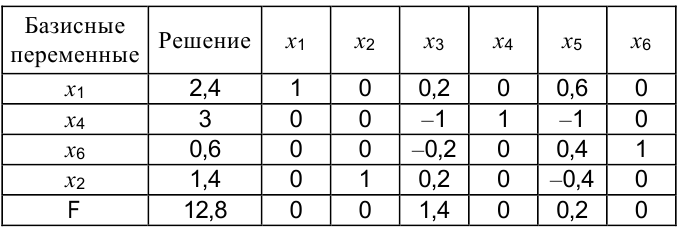
Итоговая симплекс-таблица позволяет ответить на ряд вопросов, касающихся анализа на чувствительность:
- Остаточные (балансовые или дополнительные) переменные
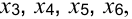 позволяют определить статус ресурсов. Если значение остаточной переменной равно нулю (
позволяют определить статус ресурсов. Если значение остаточной переменной равно нулю (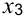 и
и 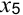 ), то ресурс израсходован полностью, т. е. является дефицитным.
), то ресурс израсходован полностью, т. е. является дефицитным.
Положительное значение остаточной переменной (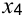 = 3,
= 3, 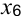 = 0,6) говорит о недефицитности соответствующего ресурса. Это и есть величина избытка. Соответствующие ресурсы можно уменьшить на полученную величину без изменения значения ЦФ.
= 0,6) говорит о недефицитности соответствующего ресурса. Это и есть величина избытка. Соответствующие ресурсы можно уменьшить на полученную величину без изменения значения ЦФ.
- Теневая цена ресурсов указана в последней строке симплекс-таблицы. Наиболее выгодный — первый ресурс (сырье А, ему соответствует переменная
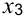 ), т. к. он имеет наибольшую теневую цену
), т. к. он имеет наибольшую теневую цену 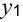 = 1,4. Поэтому дополнительные капиталовложения в первую очередь следует направлять на увеличение запаса сырья А (первый ресурс) и лишь затем — на формирование разницы в спросе на продукцию
= 1,4. Поэтому дополнительные капиталовложения в первую очередь следует направлять на увеличение запаса сырья А (первый ресурс) и лишь затем — на формирование разницы в спросе на продукцию 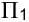 и
и  .
. - Максимальное изменение запаса ресурса.
Пусть запас первого ресурса (сырье А) изменится на величину 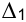 , тогда результирующая симплекс-таблица примет следующий вид:
, тогда результирующая симплекс-таблица примет следующий вид:
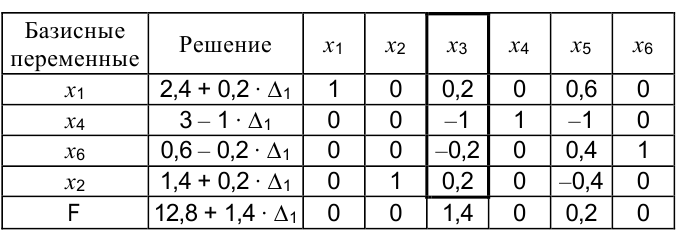
Так как изменение величины ресурса сказывается только на элементах столбца «Решение», то это может повлиять только на допустимость решения, поэтому должна выполняться система

Решая систему неравенств, получим: -7 < 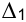 < 3. Таким образом, уменьшение запаса сырья А (первый ресурс) более чем на 7 единиц или увеличение более чем на 3 единицы приведет к недопустимости полученного решения и новой совокупности базисных переменных. Внутри указанного интервала решение будет действительным. Запас сырья А должен быть в следующих пределах:
< 3. Таким образом, уменьшение запаса сырья А (первый ресурс) более чем на 7 единиц или увеличение более чем на 3 единицы приведет к недопустимости полученного решения и новой совокупности базисных переменных. Внутри указанного интервала решение будет действительным. Запас сырья А должен быть в следующих пределах:
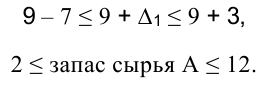
Вывод: запас сырья А можно увеличить на 3 единицы с 9 до 12, это приведет к увеличению ЦФ с 12,8 до 17 единиц (12,8+1,4-3 = 17).
- Анализ на чувствительность оптимального решения к изменению коэффициентов ЦФ.
Пусть доход, получаемый с единицы продукции 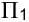 , изменится на величину
, изменится на величину 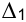 , тогда итоговая симплекс-таблица примет следующий вид:
, тогда итоговая симплекс-таблица примет следующий вид:
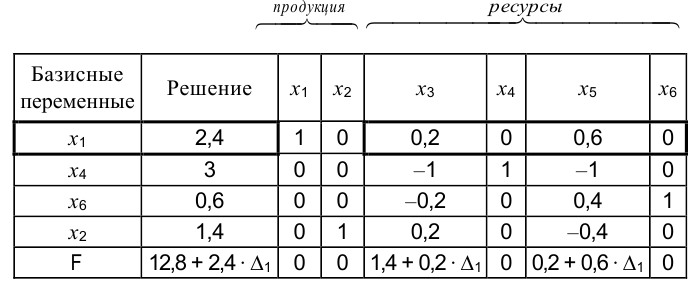
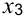 и
и 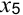 не вошли в базис, должно выполняться:
не вошли в базис, должно выполняться:
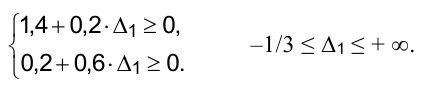
При изменении цены на первый вид продукции от 8/3 до 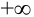 оптимальные значения переменных останутся неизменными:
оптимальные значения переменных останутся неизменными:
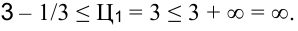
Возможно эта страница вам будет полезна:
| Решение задач по ЭММ |
Экономическая интерпретация двойственности
Задача, двойственная к задаче об ассортименте продукции, рассмотренной в примере 1.1, имеет вид:
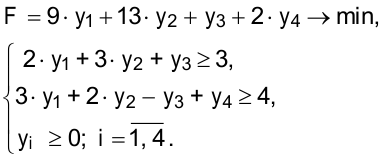
Аналогично как и для прямой задачи, двойственную задачу представляют в каноническом виде, т. е. вводят дополнительные переменные  которые прибавляют к левым частям соответствующих неравенств. В целевую функцию все дополнительные переменные вводят с коэффициентами, равными нулю.
которые прибавляют к левым частям соответствующих неравенств. В целевую функцию все дополнительные переменные вводят с коэффициентами, равными нулю.
Решая двойственную задачу симплекс-методом, получим следующую итоговую таблицу:
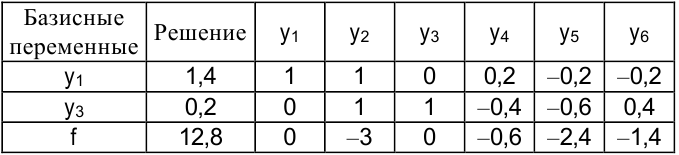
Переменные 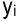 двойственной задачи называют двойственными оценками, они представляют собой теневые цены соответствующих ресурсов прямой задачи.
двойственной задачи называют двойственными оценками, они представляют собой теневые цены соответствующих ресурсов прямой задачи.
Анализ на чувствительность оптимального решения базируется на следующих свойствах двойственных оценок (ДО):
- ДО характеризуют дефицитность ресурсов: чем больше значение ДО, тем более дефицитным является ресурс. Для не-дефицитных ресурсов
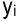 = 0.
= 0. - ДО показывают, как влияют изменения в правой части ограничений (запасов ресурсов) на значение ЦФ.
Практический интерес представляет верхняя и нижняя границы изменения ресурсов, в которых значения оценок остаются неизменными.
Для дефицитных ресурсов:
нижняя граница:
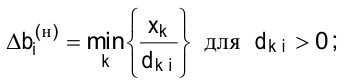
верхняя граница:
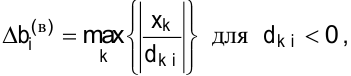
где 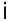 — номер ресурса;
— номер ресурса;
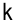 — индекс базисной переменной;
— индекс базисной переменной; 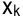 — оптимальное значение базисной переменной;
— оптимальное значение базисной переменной; 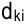 — элементы матрицы коэффициентов при базисных переменных в итоговой симплекс-таблице прямой задачи.
— элементы матрицы коэффициентов при базисных переменных в итоговой симплекс-таблице прямой задачи.
Для примера 1.1 для дефицитных ресурсов (см. итоговую табл. пункта 1.3):
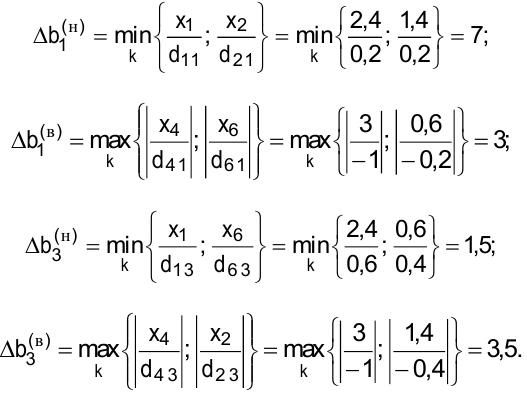
Для недефицитных ресурсов верхняя граница интервала устойчивости определяется исходными данными, а нижняя равна величине фактически израсходованных ресурсов.
Таким образом, интервалы устойчивости оценок по отношению к изменению ресурсов будут равны:

Если изменения запасов ресурсов находятся в пределах устойчивости двойственных оценок, их раздельное влияние на значение ЦФ равно произведению двойственной оценки и величины изменения запасов ресурса.
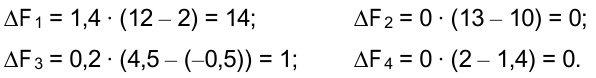
Суммарное возможное увеличение ЦФ составит:
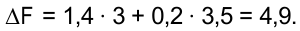
- ДО являются показателем эффективности производства отдельных видов продукции с точки зрения критерия оптимальности. С этой позиции в оптимальный план может быть включена лишь та продукция, для которой выполняется условие
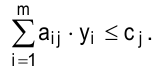
Например, введение в план третьего вида продукции с технологическими коэффициентами 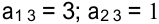 и ценой
и ценой 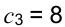 выгодно, поскольку выполняется условие:
выгодно, поскольку выполняется условие:
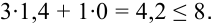
Математическая модель задачи примет следующий вид:
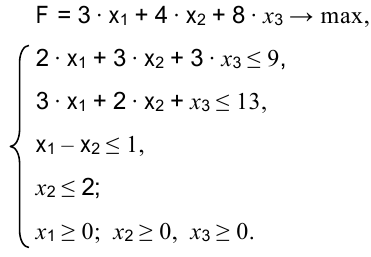
- ДО позволяют производить сравнение суммарных условных затрат и результатов. Так, например, приобретение двух единиц первого ресурса (сырье А) по цене
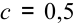 денежных единиц целесообразно, т. к.:
денежных единиц целесообразно, т. к.:
а) изменение ресурса находится в пределах устойчивости ДО;
б) 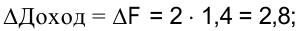
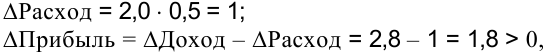
т. е. прибыль увеличивается.
Возможно эта страница вам будет полезна:
| Помощь по экономико математическим методам |
Задача №2
На предприятии выпускают 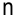 видов продукции
видов продукции 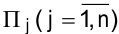 . При ее изготовлении используются ресурсы
. При ее изготовлении используются ресурсы 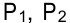 и
и 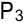 . Размеры допустимых затрат ресурсов ограничены соответственно величинами
. Размеры допустимых затрат ресурсов ограничены соответственно величинами 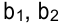 и
и  . Расход ресурса
. Расход ресурса 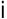 -го вида
-го вида 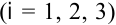 на единицу продукции
на единицу продукции 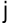 -го вида составляет
-го вида составляет  денежных единиц. Цена единицы продукции
денежных единиц. Цена единицы продукции 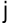 -го вида равна
-го вида равна 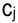 денежных единиц.
денежных единиц.
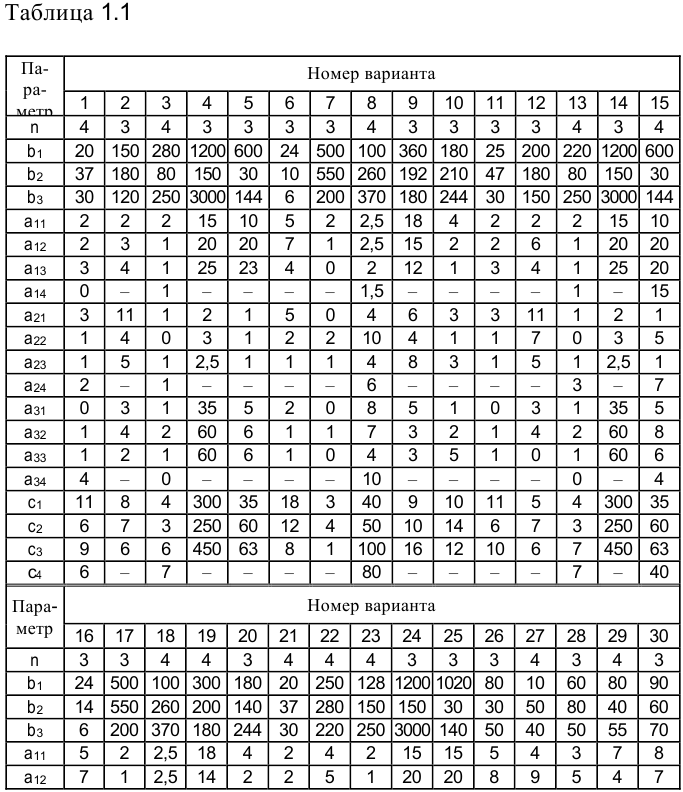
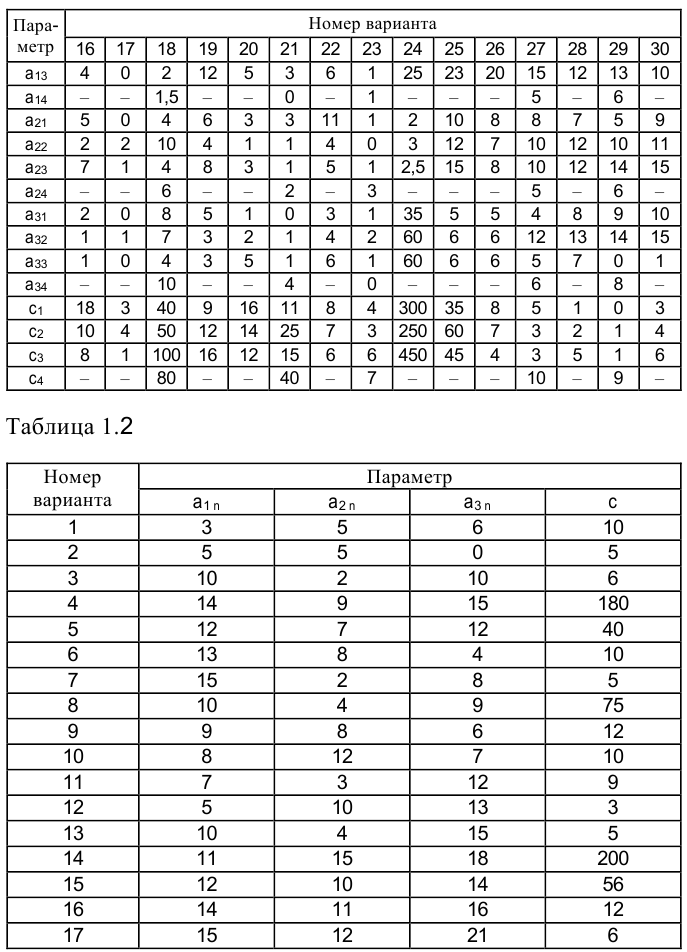
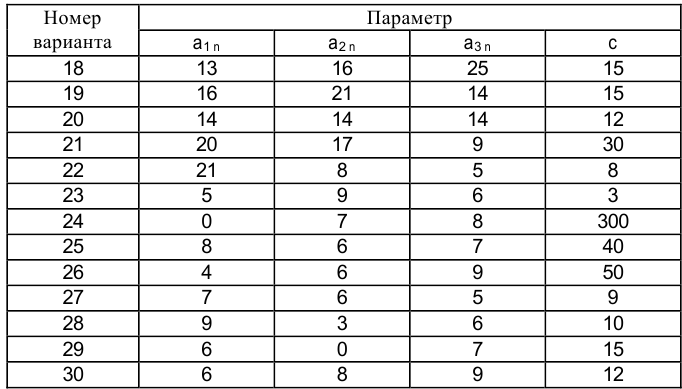
Задание, соответствующее номеру варианта (по порядковому номеру в списке группы), приведено в таблицах 1.1, 1.2.
Требуется:
1) составить математическую модель задачи, позволяющую найти сбалансированный план выпуска продукции, обеспечивающий предприятию максимальный доход;
2) найти оптимальный план выпуска продукции каждого вида симплекс-методом (дать содержательный ответ, раскрыв экономический смысл всех переменных, приведенных в решении задачи);
3) составить математическую модель двойственной задачи и определить ее решение по итоговой симплекс-таблице исходной задачи;
4) определить статус ресурсов и теневую цену всех ресурсов, найти наиболее выгодный ресурс;
5) определить максимальное изменение запаса каждого ресурса;
6) определить пределы изменения каждого коэффициента целевой функции;
7) с помощью двойственных оценок определить верхнюю и нижнюю границы изменения запаса каждого ресурса (найти 14 интервалы устойчивости оценок по отношению к изменению ресурсов);
8) определить, выгодно ли введение в план производства нового вида продукции с технологическими коэффициентами 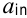 и ценой
и ценой 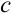 , представленными в таблице 1.2.
, представленными в таблице 1.2.
Возможно эта страница вам будет полезна:
| Курсовая работа по экономико математическим методам |
Транспортные модели. Транспортная задача и ее особенности
При планировании перевозок однородных грузов от поставщика к потребителям, что широко используется в энергетике, возникают вопросы наиболее рациональной их организации.
Часто требуется найти такой план перевозок, при котором стоимость перевозок была бы минимальной. Такая задача называется транспортной задачей (ТЗ) по критерию стоимости.
В общем виде транспортная задача формулируется так: имеется 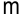 поставщиков и
поставщиков и 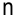 потребителей однородного груза. Запасы
потребителей однородного груза. Запасы 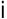 -го поставщика обозначим
-го поставщика обозначим 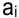 , спрос
, спрос 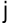 -го потребителя —
-го потребителя — 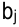 . Если обозначить
. Если обозначить 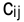 — стоимость перевозки единицы груза, а
— стоимость перевозки единицы груза, а 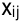 -количество перевозимого груза от
-количество перевозимого груза от 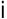 -го поставщика
-го поставщика 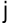 -му потребителю, то математическая модель задачи будет иметь следующий вид:
-му потребителю, то математическая модель задачи будет иметь следующий вид:
1) суммарные запасы на перевозку должны быть минимальные:
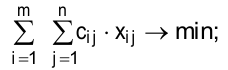
2) объем поставок 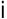 -го поставщика равен его запасу:
-го поставщика равен его запасу:
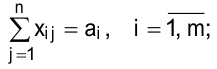
3) объем поставок 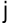 -му потребителю равен его спросу:
-му потребителю равен его спросу:
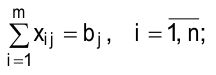
4) неотрицательность переменных:
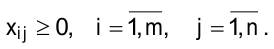
Вместо матрицы затрат 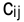 может задаваться матрица расстояний
может задаваться матрица расстояний 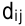 .
.
Если суммарный объем отправляемых грузов равен потребности в этих грузах, то ТЗ называется закрытой (сбалансированной):
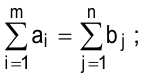
иначе — открытой.
Если имеет место открытая ТЗ, ее нужно свести к закрытой форме следующим образом:
1) если спрос превышает предложение, то вводят фиктивного поставщика с недостающим объемом спроса; тарифы 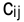 , связывающие фиктивные пункты с реальными, равны штрафам за недопоставку продукции;
, связывающие фиктивные пункты с реальными, равны штрафам за недопоставку продукции;
2) если спрос меньше предложения, то вводят фиктивного потребителя с недостающим объемом потребления; элементы матрицы 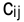 , связывающие фиктивные пункты с реальными, равны стоимости хранения единицы нераспределенного груза.
, связывающие фиктивные пункты с реальными, равны стоимости хранения единицы нераспределенного груза.
Если указанные в п. 1, 2 затраты неизвестны, то соответствующие элементы 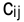 = 0.
= 0.
Транспортная задача решается в два этапа. Сначала необходимо найти исходный опорный план, а затем производится последовательно его улучшение до получения оптимального плана. На первом этапе для распределения ресурсов можно использовать правило «северо-западного угла» (здесь не учитываются тарифы и план далек от оптимального) или правило «минимального элемента», при котором необходимо осуществлять максимальные поставки ресурсов в клетки с минимальными тарифами. На втором этапе можно применить распределительный метод или метод потенциалов.
Возможно эта страница вам будет полезна:
| Контрольная по экономико математическим методам |
Метод потенциалов
Каждому поставщику (ограничению по запасам) поставим в соответствие потенциал 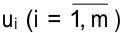 , а каждому потребителю (ограничению по спросу) — потенциал
, а каждому потребителю (ограничению по спросу) — потенциал 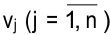 .
.
Согласно теореме о потенциалах, каждой занятой клетке будет соответствовать уравнение 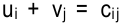 . Так как всех занятых клеток должно быть
. Так как всех занятых клеток должно быть 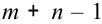 , т. е. на единицу меньше числа потенциалов, то для определения чисел
, т. е. на единицу меньше числа потенциалов, то для определения чисел 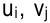 необходимо решить систему из
необходимо решить систему из 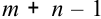 уравнений с
уравнений с 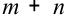 неизвестными:
неизвестными: 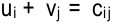 . Одному из потенциалов задают обычно значение, равное нулю.
. Одному из потенциалов задают обычно значение, равное нулю.
Для исследования плана на оптимальность по каждой свободной клетке проверяется условие 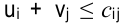 . Если хотя бы одна свободная клетка не удовлетворяет данному условию, то опорный план не является оптимальным, его можно улучшить за счет загрузки этой клетки. Если таких клеток несколько, то наиболее перспективной для загрузки является клетка, для которой разность (оценка) между тарифом клетки и суммой потенциалов наименьшая, т. е.
. Если хотя бы одна свободная клетка не удовлетворяет данному условию, то опорный план не является оптимальным, его можно улучшить за счет загрузки этой клетки. Если таких клеток несколько, то наиболее перспективной для загрузки является клетка, для которой разность (оценка) между тарифом клетки и суммой потенциалов наименьшая, т. е.
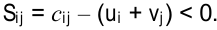
Например, для клеток 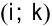 и
и 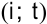 имеем оценки:
имеем оценки: 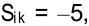
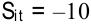 . Здесь наиболее потенциальной является клетка
. Здесь наиболее потенциальной является клетка 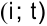 . Экономически оценка показывает, на сколько денежных единиц уменьшатся транспортные издержки от загрузки данной клетки единицей груза. Эффективность плана от загрузки потенциальной клетки грузом в
. Экономически оценка показывает, на сколько денежных единиц уменьшатся транспортные издержки от загрузки данной клетки единицей груза. Эффективность плана от загрузки потенциальной клетки грузом в 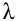 единиц составит
единиц составит 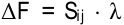 денежных единиц. Если для всех свободных клеток оценки
денежных единиц. Если для всех свободных клеток оценки 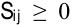 , то опорный план перевозок является оптимальным.
, то опорный план перевозок является оптимальным.
Итак, если для опорного плана перевозок указанное условие оптимальности не выполняется, то за счет загрузки свободной клетки с отрицательной оценкой план перевозок улучшается. Для наиболее перспективной свободной клетки строится замкнутый цикл с вершинами в загруженных клетках. Вершинам этого цикла условно приписываются знаки: свободной клетке — плюс, следующей по часовой или против часовой стрелки занятой клетке — минус, следующей — снова плюс и т. д. Из поставок в клетках цикла с «отрицательными» вершинами выбирается наименьшее количество 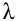 груза, которое и перемещается по клеткам этого цикла: прибавляется к поставкам в положительных вершинах и вычитается из поставок в отрицательных вершинах, в результате чего баланс цикла не нарушится.
груза, которое и перемещается по клеткам этого цикла: прибавляется к поставкам в положительных вершинах и вычитается из поставок в отрицательных вершинах, в результате чего баланс цикла не нарушится.
Сформулируем алгоритм решения ТЗ методом потенциалов:
1) построить опорный план по одному из правил;
2) вычислить потенциалы поставщиков и потребителей 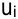 и
и 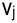
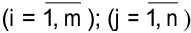 , решив систему уравнений вида
, решив систему уравнений вида 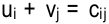 ;
;
3) вычислить оценки 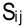 для всех свободных клеток по формуле
для всех свободных клеток по формуле 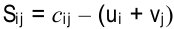 . Если все
. Если все 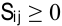 , то полученный план является оптимальным. При этом если все
, то полученный план является оптимальным. При этом если все 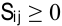 , то полученный оптимальный план единственный. В случае, если хотя бы одна оценка
, то полученный оптимальный план единственный. В случае, если хотя бы одна оценка 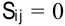 , имеем бесчисленное множество оптимальных планов с одним и тем же значением целевой функции.
, имеем бесчисленное множество оптимальных планов с одним и тем же значением целевой функции.
Возможно эта страница вам будет полезна:
| Заказать работу по экономико математическим методам |
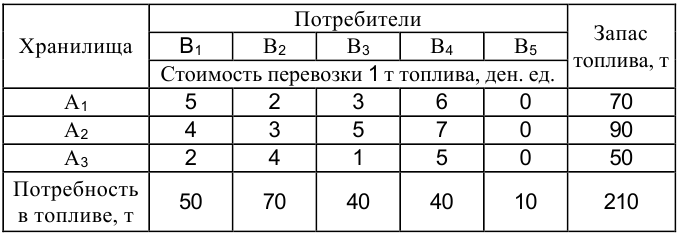
Задача №2.1.
В трех хранилищах 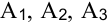 имеется соответственно 70, 90 и 50 т топлива. Требуется спланировать перевозку топлива четырем потребителям
имеется соответственно 70, 90 и 50 т топлива. Требуется спланировать перевозку топлива четырем потребителям 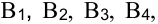 спрос которых равен соответственно 50, 70, 40 и 40 т, так, чтобы затраты на транспортировку были минимальны. Стоимость перевозки 1 т указана в таблице.
спрос которых равен соответственно 50, 70, 40 и 40 т, так, чтобы затраты на транспортировку были минимальны. Стоимость перевозки 1 т указана в таблице.
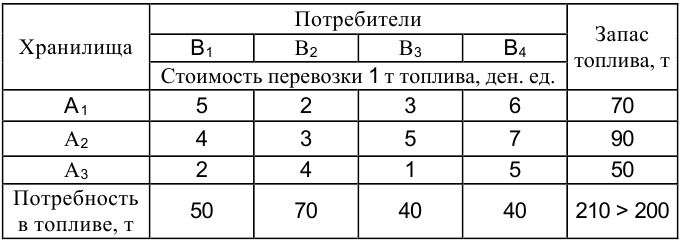
Решение:
Поскольку запасы топлива в хранилищах превышают спрос потребителей, задача является открытой, вводится фиктивный потребитель, спрос которого 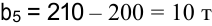 .
.
Все затраты для фиктивного потребителя 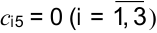 . После введения фиктивного потребителя открытая модель задачи преобразовалась в закрытую, а распределительная таблица принимает следующий вид:
. После введения фиктивного потребителя открытая модель задачи преобразовалась в закрытую, а распределительная таблица принимает следующий вид:
Исходный опорный план получим, например, по правилу «минимального элемента». Так как наименьшими являются нулевые тарифы для клеток (1; 5), (2; 5), (3; 5), то загрузим первой, например, клетку (1; 5), 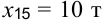 . Второй загружаем клетку (3; 3),
. Второй загружаем клетку (3; 3), 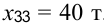 . Далее загружаем клетки (1; 2), (3; 1), (2; 2), (2; 4), Полагая
. Далее загружаем клетки (1; 2), (3; 1), (2; 2), (2; 4), Полагая
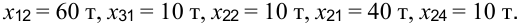
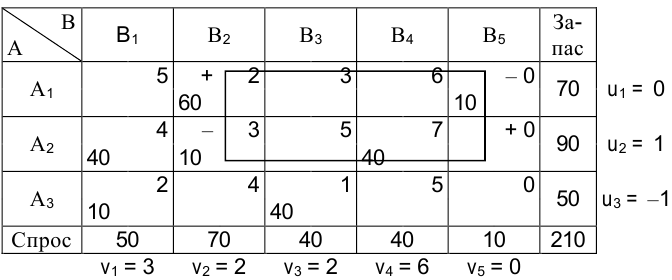
В результате распределения топлива по потребителям получили невырожденный план: условие для занятых клеток
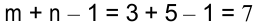
выполняется.
Для определения потенциалов составляем уравнения для занятых клеток:
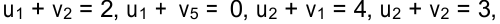
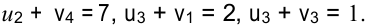
Положим, например,
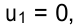
тогда
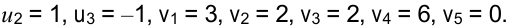
Определим оценки свободных клеток:
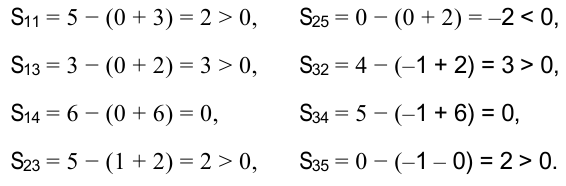
Определив потенциалы, устанавливаем, что среди оценок свободных клеток одна отрицательная: 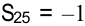 , следовательно, план перевозок можно улучшить за счет загрузки клетки (2; 5). Цикл для нее выделен линией в предыдущей таблице.
, следовательно, план перевозок можно улучшить за счет загрузки клетки (2; 5). Цикл для нее выделен линией в предыдущей таблице.
Наименьшее количество топлива в отрицательных вершинах цикла равно 10 т. После смещения по циклу 10 т получаем новый план перевозок. Полученный план является вырожденным. Поставим число 0, например, в клетку (2; 2).
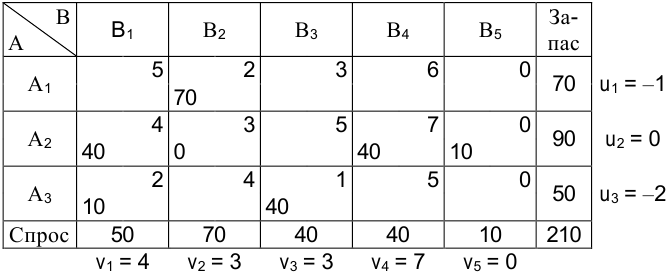
Для нового плана определяем новые потенциалы и находим оценки свободных клеток:
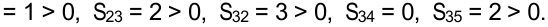
Оценки всех свободных клеток 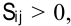 следовательно, получен оптимальный план. Поскольку среди оценок имеются равные нулю, то за счет загрузки клеток (1; 4), (3; 4) можно получить новые планы, но значение целевой функции не изменится. Это случай бесчисленного множества оптимальных планов.
следовательно, получен оптимальный план. Поскольку среди оценок имеются равные нулю, то за счет загрузки клеток (1; 4), (3; 4) можно получить новые планы, но значение целевой функции не изменится. Это случай бесчисленного множества оптимальных планов.
Итак, в предыдущей таблице получили оптимальный план

для которого значение целевой функции равно
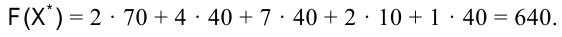
Десять тонн топлива, находящегося в хранилище 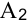 , осталось нераспределенным.
, осталось нераспределенным.
Транспортные задачи в усложненной постановке
Рассмотренная выше постановка ТЗ в экономике предприятия встречается редко. Для того, чтобы свести задачу к задаче транспортного типа, приходится учитывать ряд дополнительных ограничений:
- Отдельные поставки от определенных поставщиков некоторым потребителям должны быть исключены из-за отсутствия необходимых условий хранения, чрезмерной загрузки транспортных коммуникаций и т. д. Это достигается путем искусственного завышения тарифов в тех ячейках транспортной таблицы, перевозки через которые следует запретить.
- На предприятии необходимо оценить суммарные затраты на производство и транспортировку продукции. С подобной задачей сталкиваются при планировании размещения производственных объектов. С этой точки зрения может оказаться экономически более выгодным поставлять сырье из более отдаленных регионов, но по меньшей его себестоимости. В таких задачах в качестве критерия оптимальности принимают суммарные затраты на транспортировку и производство продукции (в транспортной таблице к стоимости перевозки добавляется себестоимость изготовления продукции).
- Ряд транспортных маршрутов, по которым необходимо доставить груз, имеет ограничения по пропускной способности (ограничение «не более чем»).
Например, если по маршруту 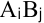 можно доставить не более чем
можно доставить не более чем 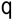 единиц груза, столбец
единиц груза, столбец 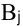 разбивается на два столбца:
разбивается на два столбца: 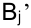 и
и 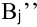 . В первом спрос равен
. В первом спрос равен 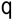 , во втором —
, во втором — 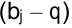 .
.
Несмотря на то, что транспортные затраты в обоих столбцах одинаковы и равны исходным, ячейка 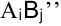 блокируется (в ней ставится завышенный тариф).
блокируется (в ней ставится завышенный тариф).
- Поставки по определенным маршрутам обязательны и должны войти в план поставок независимо от того, выгодно это или нет (ограничение «не менее чем»). В этом случае уменьшают запас груза и спрос у соответствующих поставщиков и потребителей на величину обязательных поставок и решают задачу относительно тех поставок, которые необязательны. После чего задачу корректируют с учетом обязательных поставок.
- Необходимо максимизировать целевую функцию в ТЗ. Для этого надо изменить знак в тарифах на противоположный.
Задача №3
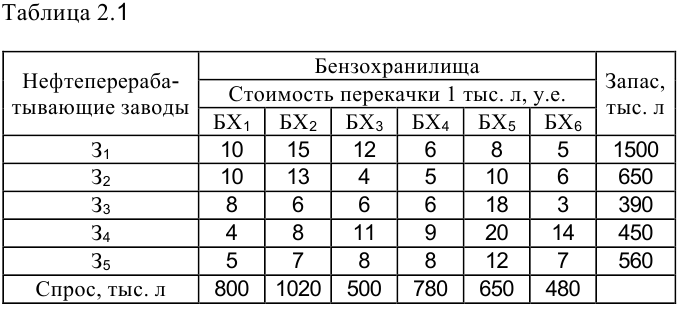
Задание, соответствующее номеру варианта (по порядковому номеру в списке группы), приведено в таблицах 2.1, 2.2.
Нефтеперерабатывающие заводы 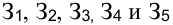 ежедневно производят бензин, который направляется в бензохранилища
ежедневно производят бензин, который направляется в бензохранилища 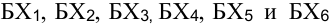 . Объем производства бензина и вместимость бензохранилищ представлены в таблице 2.1. Все бензохранилища связаны с заводами трубопроводами, по которым и перекачивается бензин. Стоимость перекачки 1 тыс. л бензина с заводов в бензохранилища приведена в таблице 2.1. Себестоимость 1 тыс. л бензина на нефтеперерабатывающих заводах соответственно равна 7, 4, 5, 8, 8 у. е.
. Объем производства бензина и вместимость бензохранилищ представлены в таблице 2.1. Все бензохранилища связаны с заводами трубопроводами, по которым и перекачивается бензин. Стоимость перекачки 1 тыс. л бензина с заводов в бензохранилища приведена в таблице 2.1. Себестоимость 1 тыс. л бензина на нефтеперерабатывающих заводах соответственно равна 7, 4, 5, 8, 8 у. е.
При этом необходимо учитывать, что из-за ремонтных работ временно нет возможности перевозить бензин с некоторых заводов в бензохранилища. В таблице 2.2 это показано в столбце «Запрет поставки» в формате [№ завода х № бензохранилища]. Например, «2×3» обозначает, что нельзя перевозить бензин с завода № 2 в бензохранилище № 3.
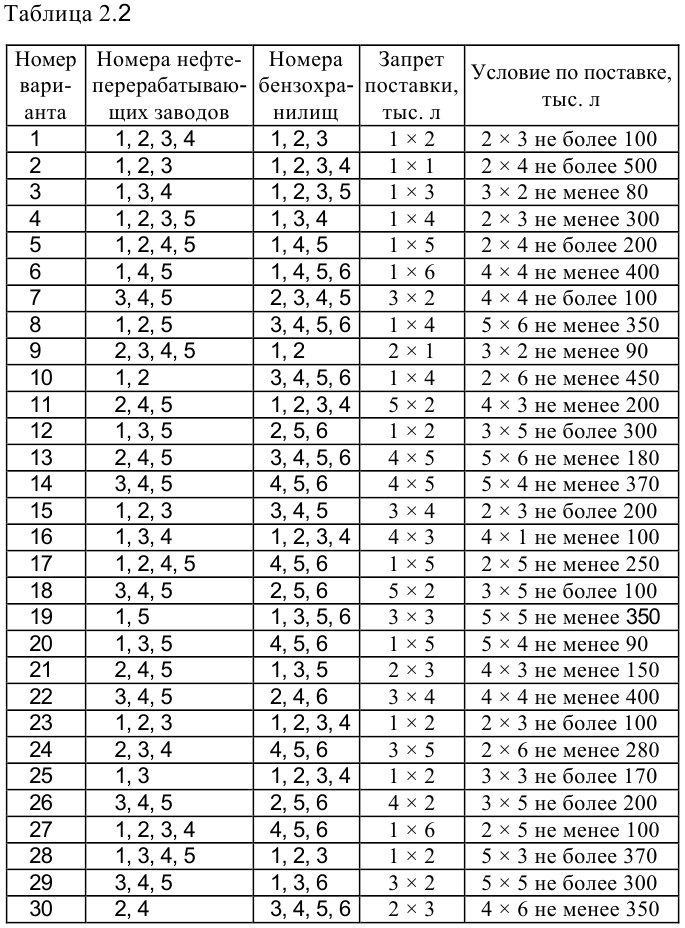
Кроме того, необходимо учесть, что некоторые бензохранилища имеют договоры на гарантированную поставку бензина с определенных заводов в определенных объемах (условия «не более» или «не менее»), В таблице 2.2 это показано в столбце «Условие по поставке» в формате [№ завода х № бензохранилища «не более» / «не менее» объем поставки]. Например, «1×4 не менее 40» обозначает, что между заводом № 1 и бензохранилищем № 4 заключен договор на поставку не менее 40 тыс. л бензина.
Требуется составить план перекачки бензина с заводов в бензохранилища, обеспечивающий минимальные затраты.
Необходимо:
- составить транспортную таблицу, позволяющую найти план перевозки бензина с заводов
 в бензохранилища
в бензохранилища 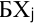 , отразив в ней все дополнительные условия ‘,
, отразив в ней все дополнительные условия ‘, - найти исходный опорный план перевозки бензина;
- решить задачу методом потенциалов, сформулировать вывод относительно распределения поставок бензина;
- вычислить величину
 минимальных суммарных затрат на производство и доставку бензина;
минимальных суммарных затрат на производство и доставку бензина; - назвать пункты, в которых остается нераспределенная продукция, и указать объемы такой продукции.
Методы сетевого планирования и управления (мспиу). Построение сети проекта
При планировании сложных комплексов взаимосвязанных работ актуально использование МСПиУ.
Основой МСПиУ является сетевой график (сетевая модель), которая отражает логическую взаимосвязь и логическую взаимообусловленность всех входящих в проект элементарных операций (работ).
Различают три вида событий: исходное — соответствует началу выполнения проекта, не имеет предшествующих работ; завершающее — соответствует достижению конечной цели, не имеет последующих работ; промежуточное — все остальные события.
Пока не будут завершены все входящие в событие работы, не может свершиться само событие и, следовательно, не может быть начата ни одна из выходящих из этого события работа. Событие — это момент времени, когда завершаются одни работы и начинаются другие.
Событие представляет собой результат проведенных работ и, в отличие от работ, не имеет протяженности во времени.
Существует три вида работ (операций):
 действительная: работа, которая требует затрат
действительная: работа, которая требует затрат
времени и ресурсов, например, разработка проекта, выполнение СМР и т. д.;
2)  операция ожидания: процесс, требующий только затрат времени, например, затвердевание бетона, естественная сушка краски и т. д.;
операция ожидания: процесс, требующий только затрат времени, например, затвердевание бетона, естественная сушка краски и т. д.;
3)  фиктивная работа или логическая зависимость:
фиктивная работа или логическая зависимость:
отражает ресурсную или логическую зависимость при выполнении некоторых операций. Фиктивная работа имеет нулевую продолжительность.
Работа называется критической, если она должна начинаться и заканчиваться в строго отведенное время, т. е. не имеет резерва времени своего начала и окончания, который не влиял бы на продолжительность выполнения всего проекта.
Для некритических работ возможен некоторый сдвиг времени их начала, но в определенных пределах, которые не влияют на срок выполнения всего проекта.
При построении сетевого графика необходимо следовать правилам: длина стрелки не зависит от времени выполнения работы; стрелка может не быть прямолинейным отрезком; для действительных работ используются сплошные, а для фиктивных — пунктирные стрелки; каждая операция должна быть представлена только одной стрелкой; между одними и теми же событиями не должно быть параллельных работ, т. е. работ с одинаковыми кодами; следует избегать пересечения стрелок; не должно быть стрелок, направленных справа налево; номер начального события должен быть меньше номера конечного события; не должно быть висячих событий (т. е. не имеющих предшествующих событий), кроме исходного; не должно быть тупиковых событий (т. е. не имеющих последующих событий), кроме завершающего; не должно быть циклов.
Анализ проектов методом критического пути. Расчет временных параметров сетевого графика. График Ганта
Введем следующие обозначения:
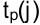 — самое раннее возможное время свершения
— самое раннее возможное время свершения 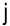 -го события;
-го события;
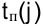 — самое позднее возможное время свершения
— самое позднее возможное время свершения 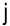 -го события;
-го события;
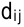 — длительность работы
— длительность работы 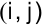 .
.
Расчет временных параметров сетевого графика проходит в два этапа:
- Вычисляются ранние сроки свершения событий.
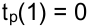 . Для узла
. Для узла 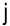 определим узлы
определим узлы 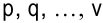 , которые связаны с узлом
, которые связаны с узлом 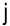 работами
работами 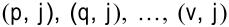 и для которых уже вычислены самые ранние сроки свершения начальных событий, тогда
и для которых уже вычислены самые ранние сроки свершения начальных событий, тогда
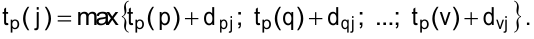
Первый этап заканчивается, когда будет вычислен 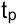 последнего
последнего 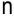 -го события.
-го события. 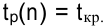 . Критический путь — наибольший путь от начального события до завершающего.
. Критический путь — наибольший путь от начального события до завершающего.
- Вычисляются поздние сроки свершения событий.
Полагаем, что
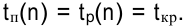
Для узла 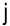 определим узлы
определим узлы 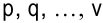 , которые связаны с узлом
, которые связаны с узлом 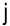 работами
работами 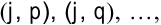
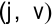 и для которых уже вычислены самые поздние сроки свершения соответствующих событий
и для которых уже вычислены самые поздние сроки свершения соответствующих событий
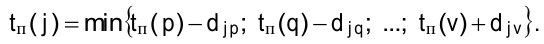
Второй этап заканчивается, когда будет вычислено
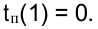
Резервы времени событий:
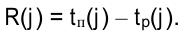
Рассчитанные численные значения временных параметров записываются прямо в вершины сетевого графика (рисунок 3.1).
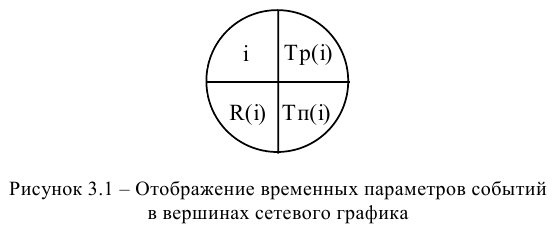
Для критических работ должна получиться непрерывная последовательность от начального события до завершающего. Сумма продолжительностей работ, лежащих на критическом пути, равна минимальному сроку выполнения проекта и равна 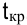 .
.
Резервы времени событий, лежащих на критическом пути, равны нулю. Для сетевого графика может быть несколько критических путей.
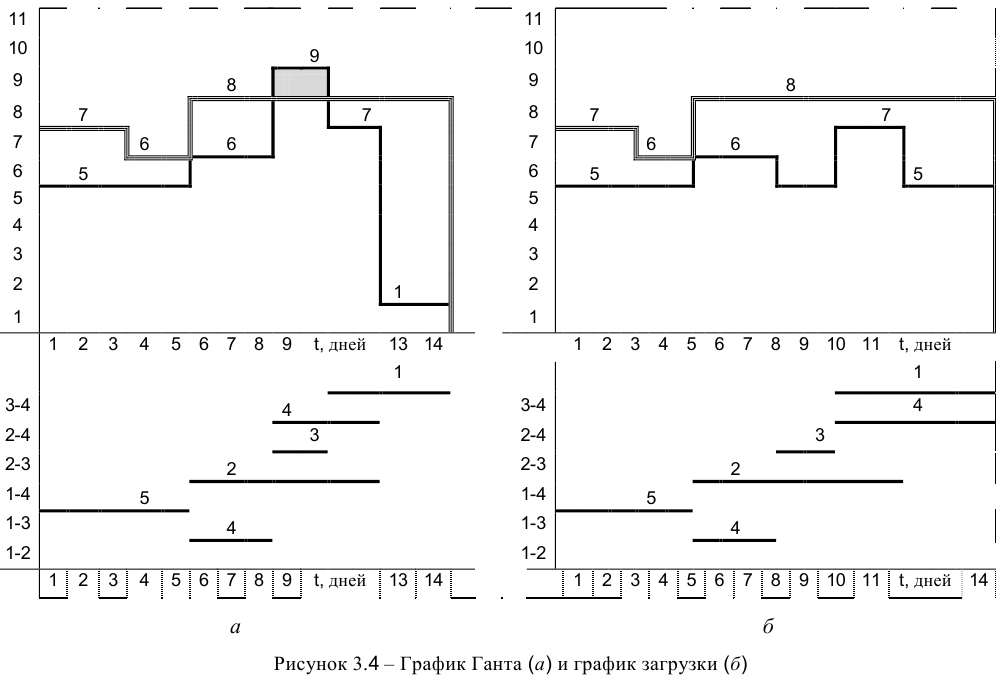
Удобным дополнением к сетевому графику является линейный график (график Ганта). На таком графике каждая работа изображается горизонтальным отрезком в привязке к оси времени, длина которого равна продолжительности выполнения работы. Начало каждой работы совпадает с ранним сроком свсршсния ее начального события. Критические работы образуют на графике Ганта непрерывный путь от начала выполнения проекта до его завершения без временных зазоров и перекрытий. Их суммарная длительность равна длительности выполнения всего проекта.
Некритические работы предпочитают начинать в самый ранний возможный срок, в этом случае остается запас времени, который можно использовать для решения неожиданно возникающих в ходе выполнения проекта проблем. Вместе с тем, можно перенести начало выполнения какого-либо некритического процесса.
Оптимизация сетевых моделей по ресурсам (исполнителям)
При оптимизации использования ресурса рабочей силы чаще всего сетевые работы стремятся организовать таким образом, чтобы количество одновременно занятых исполнителей было минимальным; выровнять потребность в людских ресурсах на протяжении срока выполнения проекта.
Суть оптимизации загрузки сетевых моделей по ресурсам заключается в следующем: необходимо таким образом организовать выполнение сетевых работ, чтобы количество одновременно работающих исполнителей было минимальным. Для проведения подобных видов оптимизации необходимо построить и проанализировать график привязки (график Ганта) и график загрузки.
График Ганта отображает взаимосвязь выполняемых работ во времени и строится на основе данных о продолжительности работ. По вертикальной оси графика привязки откладываются коды работ, по горизонтальной оси — длительность работ.
На графике загрузки по горизонтальной оси откладывается время, например в днях, по вертикальной — количество человек (ресурсов), занятых работой в каждый конкретный день.
Описанные виды оптимизации загрузки выполняются за счет сдвига во времени некритических работ, т. е. работ, имеющих полный и/или свободный резервы времени. Полный и свободный резервы любой работы можно определить без специальных расчетов, анализируя только график привязки. Сдвиг работы означает, что она будет выполняться уже в другие дни (т. е. изменится время ее начала и окончания), что в свою очередь приведет к изменению количества исполнителей, работающих одновременно (т. е. уровня ежедневной загрузки сети).
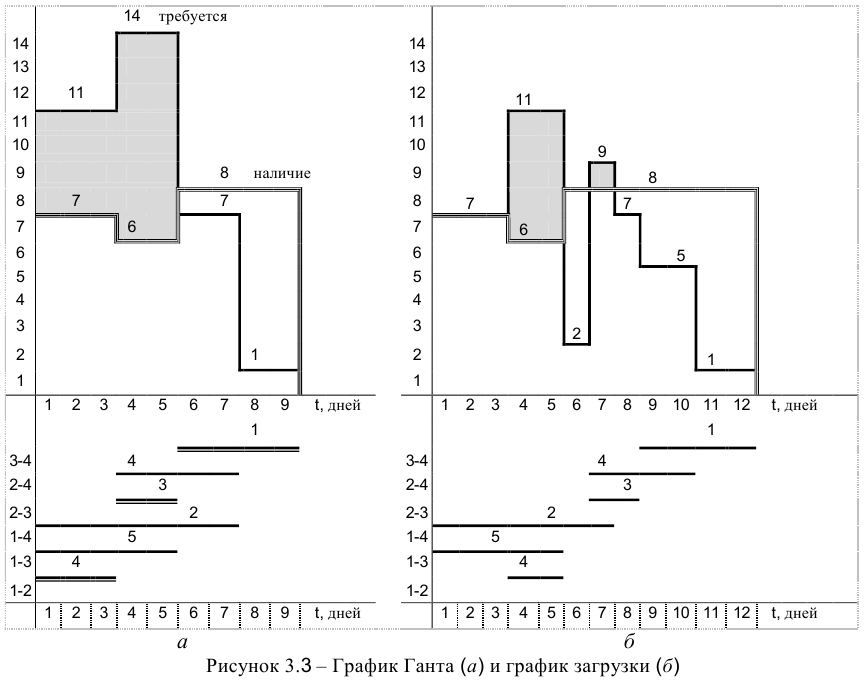
Задача №3.1.
Для выполнения комплекса операций по ремонту энергетического оборудования предприятие в первые три дня выделяет 7 единиц ресурсов (ед. рос.), в 4 и 5 дни -6 ед. рес., в последующие — 8 ед. рсс. Сетевой график представлен на рисунке 3.2. Каждой работе графика приписаны два числа: 1) временная оценка, дней; 2) интенсивность потребления ресурса, ед. рос. Работа (1, 2) — 3; 4; (1, 3) — 5; 5; (1,4)- 7; 2; (2, 3) — 2; 3; (2, 4) — 4; 4; (3, 4) — 4; 1. Определить сроки выполнения операций таким образом, чтобы завершить весь комплекс работ за минимальное время, при условии, что операции не допускают перерывов в выполнении.
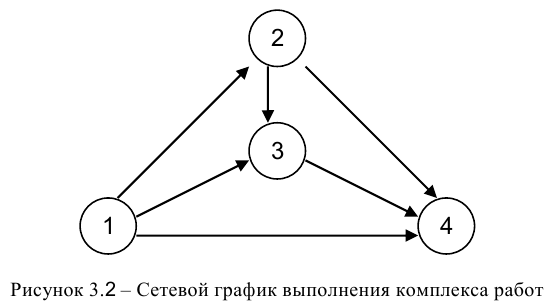
Решение:
- Рассчитав временные параметры сетевого графика, определили, что весь проект может быть выполнен за
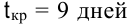 .
.
На критическом пути лежат работы (1, 2), (2, 3), (3, 4). Представим график Ганта и график загрузки на рисунке 3.3, а. Из графика загрузки видно, что в первые пять дней потребность в ресурсах больше их наличия (на графике выделено серым цветом).
Следовательно, выполнить проект за девять дней невозможно, поэтому необходимо провести оптимизацию по ресурсам, чтобы выполнить работы с помощью имеющихся ресурсов.
- Проецируем на ось времени начало и окончание каждой работы. Проекцию, совпадающую с началом координат, обозначим
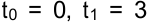 — окончание работы (1, 2). Определим полные резервы времени
— окончание работы (1, 2). Определим полные резервы времени 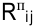 операций, расположенных на промежутке от
операций, расположенных на промежутке от 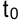 до
до 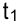 , нумеруем эти операции в порядке возрастания полных резервов. Операции с одинаковыми резервами времени нумеруют в порядке убывания интенсивности.
, нумеруем эти операции в порядке возрастания полных резервов. Операции с одинаковыми резервами времени нумеруют в порядке убывания интенсивности. 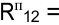
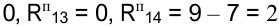 дня. Нумеруем работы по важности:
дня. Нумеруем работы по важности:
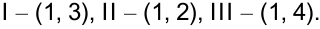
- Последовательно суммируем интенсивности работ, расположенных над промежутком от
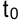 до
до 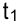 в порядке возрастания их номеров и сравниваем полученные суммы с заданной величиной имеющихся ресурсов
в порядке возрастания их номеров и сравниваем полученные суммы с заданной величиной имеющихся ресурсов 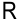 . Все операции, сумма интенсивностей которых не превышает наличие ресурсов
. Все операции, сумма интенсивностей которых не превышает наличие ресурсов 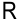 , оставляем в первоначальном положении. Если после добавления интенсивности какой-либо операции окажется, что суммарное потребление ресурсов больше
, оставляем в первоначальном положении. Если после добавления интенсивности какой-либо операции окажется, что суммарное потребление ресурсов больше 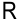 , то эту операцию сдвигают вправо на величину рассматриваемого промежутка. Переходят к добавлению интенсивности следующей операции, расположенной на промежутке от
, то эту операцию сдвигают вправо на величину рассматриваемого промежутка. Переходят к добавлению интенсивности следующей операции, расположенной на промежутке от 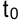 до
до 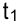 . Результатом выполнения этого действия будет новый график Ганта, момент
. Результатом выполнения этого действия будет новый график Ганта, момент 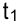 которого считаем началом оставшейся части комплекса операций (рисунок 3.3, б). Операции
которого считаем началом оставшейся части комплекса операций (рисунок 3.3, б). Операции 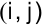 , расположенные над промежутком от
, расположенные над промежутком от 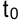 до
до 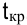 , изображают так, чтобы их начала совпадали с новыми сроками свершения событий.
, изображают так, чтобы их начала совпадали с новыми сроками свершения событий.
- Проецируем на ось времени начало и окончание операций, расположенных на промежутке от
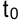 до
до 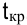 . Ближайшую к
. Ближайшую к 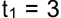 проекцию обозначим
проекцию обозначим 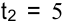 дней. Определим полные резервы операций, расположенных на промежутке от
дней. Определим полные резервы операций, расположенных на промежутке от 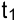 до
до 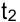 и нумеруем их. Сначала нумеруют операции, начатые левее момента
и нумеруем их. Сначала нумеруют операции, начатые левее момента 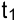 согласно возрастанию разностей между полными резервами времени этих операций и длительностью от начала до
согласно возрастанию разностей между полными резервами времени этих операций и длительностью от начала до 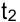 . Операции с одинаковыми разностями нумеруют в порядке убывания интенсивностей. Все остальные операции нумеруют как в п. 2. Выполняют действия, аналогичные действиям из п. 3. Если сдвигается операция, начатая левее
. Операции с одинаковыми разностями нумеруют в порядке убывания интенсивностей. Все остальные операции нумеруют как в п. 2. Выполняют действия, аналогичные действиям из п. 3. Если сдвигается операция, начатая левее 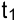 , начало се устанавливают в
, начало се устанавливают в 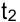 .
.
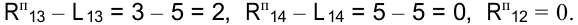
Нумеруем работы по важности:
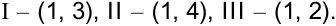
Отмечаем работы на новом графике Ганта согласно данной нумерации (рисунок 3.4, а).
Далее аналогично рассматриваем промежутки от 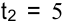
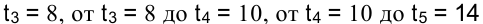
и выполняем действия пп. 2-4 (рисунок 3.4, б). После каждого графика Ганта необходимо провести проверку графика загрузки, чтобы определить, достаточно ли имеющихся ресурсов для выполнения комплекса работ.
Кстати дополнительная теория из учебников по экономико математическим методам тут.
Задача №3.2.
Задание, соответствующее номеру варианта (по порядковому номеру в списке группы), приведено в таблицах 3.1, 3.2.
Дана последовательность работ по разработке стенда.
Необходимо:
1) на основании данных таблицы 3.1 составить сетевой график комплекса работ;
2) рассчитать временные параметры графика работ, определить критический путь, назвать работы, лежащие на критическом пути;
3) построить график Ганта и график загрузки;
4) провести оптимизацию комплекса работ по ресурсам (исполнителям).