Разыскание наибольших и наименьших значений

Разыскание наибольших и наименьших значений

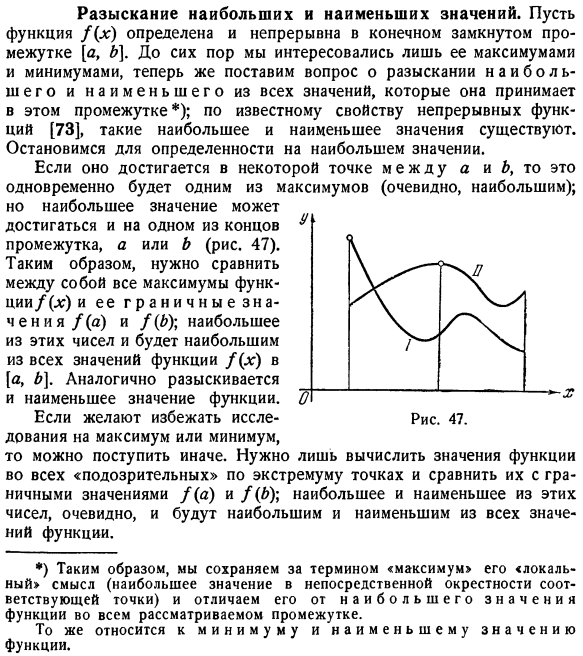
Разыскание наибольших и наименьших значений. Предположим, что функция f (q) определена и непрерывна с конечным замкнутым интервалом[a, b.Раньше его интересовали только его максимальные и минимальные значения. По известным характеристикам непрерывных функций[73] существуют такие максимумы и минимумы. Давайте подумаем об этом, чтобы прояснить максимумы. если вы достигнете в какой-то момент между a и b, это одновременно будет 1 из максимума (очевидно, максимум).Однако, максимальное значение также может быть достигнуто с помощью A или B, который является 1 на конце интервала(рис. 47). Поэтому вам нужно сравнить все максимумы функции/() и ее граничные значения/(a) и/(/)). Максимальное значение этих чисел будет максимальным значением всех значений функции/(q) из[a, b.Аналогично получается минимальное значение функции.

Таким образом, мы сохраняем термин «максимум», который обозначает значение «локальный» (максимальное значение в непосредственной близости от соответствующей точки), и отличаем его от максимального значения функции на всем рассматриваемом интервале. Людмила Фирмаль

• Если вы хотите избежать максимального или минимального опроса, вы можете сделать это в другом way. It остается только вычислить значения функций во всех «подозрительных» точках по экстремуму и сравнить их с граничными значениями f (a) и f (b).Максимальные и минимальные значения этих чисел, очевидно, являются максимальными и минимальными значениями всех значений функции. * ) То же самое относится к минимальному и минимальному значениям функции. Задача здесь мы поговорим о некоторых вопросах из разных областей. Это решение ограничивается поиском максимального или минимального значения функции. Однако во многих случаях вас интересуют сами эти значения, а не точки, которые предоставляет функция (значение аргумента).

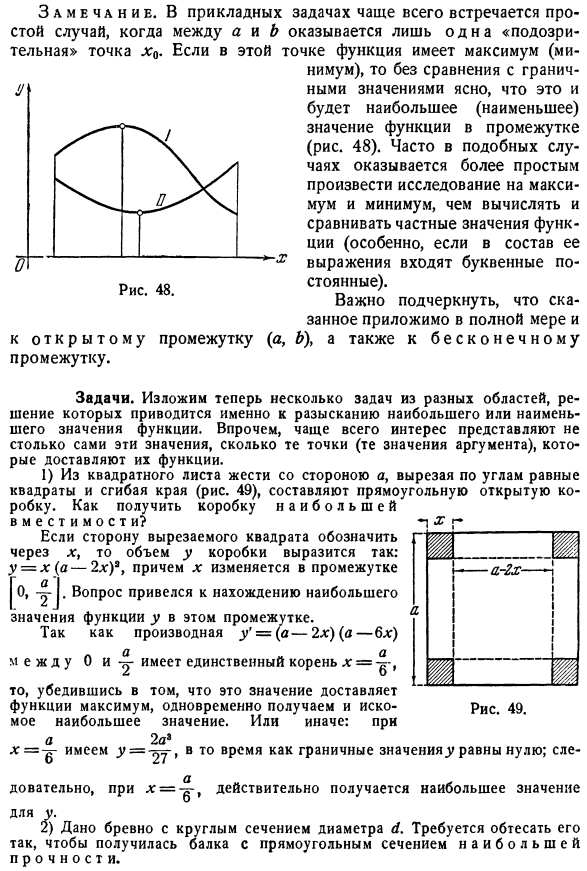
1) из квадратного листа жести на стороне а вырежьте равные квадраты по углам, отогните края(рис.49) и сделайте прямоугольную открытую коробку. Как получить коробку максимальной емкости? один： ш р р в -а-2л—! Один Один Один Один Один Один Один Я Один ш 1ш Рисунок 49. a-2n:)*, и x разнесены по-разному. Вопрос самый лучший Remarks. In в прикладной задаче наиболее часто встречаются простейшие случаи, когда между a и A имеется только 1″подозрительная» точка xy B. At в этой точке функция имеет максимум（ Понятно, что это будет максимальное (минимальное) значение функции в интервале (рис. 48), без сравнения с границей value. In во многих случаях легче найти максимальное и минимальное значения (особенно если выражение содержит символьную константу), чем вычислить и сравнить частичные значения функции.

• Важно подчеркнуть, что сказанное может быть применено в полном объеме i) и бесконечно. Открытый промежуток(а, пробел. Если стороны вырезанного квадрата обозначены xy, то объем коробки представляется следующим образом: Г = ЛГ К Значение функции y на этом интервале. Дифференциал/ =(д-2х) (о — 6Н:) С 0 до 1 корня x = Или, если нет： а 2 а * существует y= -^ -, но граничное значение равно zero. So, в случае*= фактически получается максимальное значение Y. 2) бревно с круглым поперечным сечением диаметром D было given. It необходимо обрезать его так, чтобы получилась балка прямоугольного сечения максимальной прочности. Отметим, в теории сопротивления материалов было установлено, что прочность прямоугольных балок пропорциональна произведению bH%.

Где b-основание прямоугольника балочной части, а A-его высота. = L2, то есть речь идет о максимальном значении выражения y = bH * = b(4 * br), кроме того, «независимая переменная» b изменяется с интервалами(0, 4). Производная y ’= 4 * 3b * исчезает в этом интервале на 1 раз. Поскольку производная B = 2-го порядка равна 6&0, она достигает максимального значения в указанной точке и становится максимальным значением. 4 \ H \ L-Y 3:: ^ 2: 1.Из рисунка 50 видно, как сделать необходимые прямоугольники(диаметр делится на 3 равные части, а вертикаль восстанавливается в точке деления). 3) позвольте лампочке двигаться по вертикальной прямой линии OB(например, по блоку) (рис. 51).

Далее мы проверяем, что это значение обеспечивает максимальную функцию, и в то же время получаем желаемое максимальное значение. Людмила Фирмаль

• На каком расстоянии от горизонтальной плоскости ОА должна быть расположена, чтобы получить наилучшее освещение в точке А этой плоскости? Примечание: освещение Y пропорционально$ l и обратно пропорционально расстоянию r = 2 от AB. \ \ \ \ c зависит от интенсивности света лампы накаливания. Для независимой переменной, выберите = $ ВН = р> ’ р = уя * \ АР Н −2 Диаграмма 51. * И тогда-C ’(A * + a») r>тогда производная (0 а + ОО). Л = с О * 2А *(а * + А2)6 /> 。 31Р. 消失 = -т===исчезают при 0,7 а и меняют знак при прохождении через это Вю. Значение от плюса до минуса.. Это самое выгодное расстояние. Замечания. По этому поводу обратите внимание читателя на следующее situation. To найти максимальное или минимальное значение.

Смотрите также:

Решение задач по математическому анализу

Построение графика функции.	Неопределенности вида 0/0.
Использование высших производных.	Неопределенности вида оо/оо.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.