Если разлагаемая на отрезке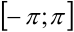 
в ряд Фурье функция 
является чётной или нечётной, то это отражается на формулах коэффициентов Фурье (вычисление их упрощается) и на виде самого ряда (он становится так называемым неполным).
Если функция — чётная, то её ряд Фурье имеет вид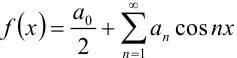 
,
где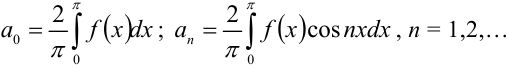 
Таким образом, ряд Фурье для чётной функции содержит свободный член и только члены с косинусами. Ряд Фурье для чётной функции называется неполным тригонометрическим рядом или рядом по косинусам.
Если функция — нечётная, то её ряд Фурье имеет вид 
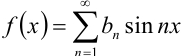, где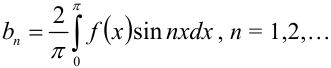 
Таким образом, ряд Фурье для нечётной функции содержит только члены с синусами. Ряд Фурье для нечётной функции называется неполным тригонометрическим рядом или рядом по синусам.
Разлагать в ряд Фурье можно и периодические функции с периодом, отличным от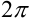 
.
Пусть функция , определённая на отрезке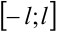 
, имеет период 
(
, 
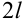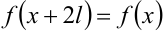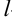— произвольное положительное число) и удовлетворяет на этом отрезке условиям теоремы Дирихле.
Тогда её разложение в ряд Фурье на отрезке 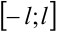имеет вид:
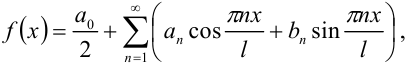
где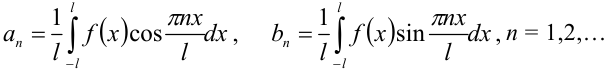 
Пример №37.3.
Разложите функцию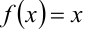 
на интервале (-4;4) в ряд Фурье.
Решение:
Функция 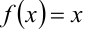удовлетворяет условиям теоремы Дирихле, поэтому она разложима в ряд Фурье. В силу нечётности функции, её ряд Фурье будет рядом по синусам. Учитывая ещё и то, что функция 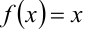— периодическая с периодом, равным 8 
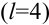, получим её разложение в ряд Фурье: 
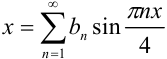, где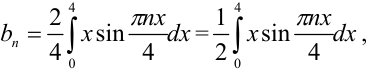 
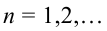Вычислим отдельно определённый интеграл 
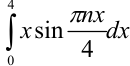методом интегрирования по частям:
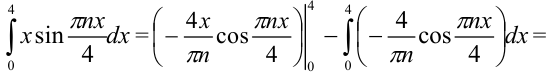
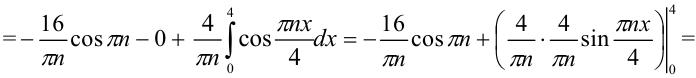
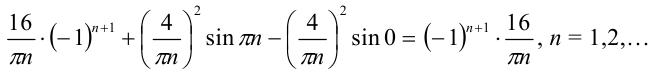
В итоге,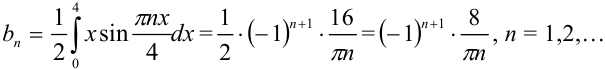 
Таким образом, разложение в ряд Фурье функции 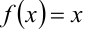имеет вид:
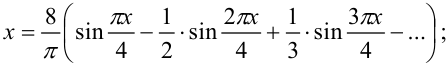
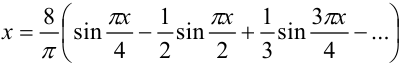
Ответ: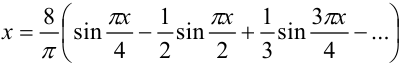
Если функция является непериодической, определённой на всей числовой оси, то она нс может быть разложена в ряд Фурье, так как сумма ряда Фурье есть функция периодическая и, следовательно, нс может быть равна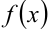 
для всех 
. Однако непериодическая функция может быть представлена в виде ряда Фурье на любом конечном промежутке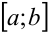 
, на котором она удовлетворяет условиям теоремы Дирихле.
Теория разложения функций в тригонометрические ряды Фурье называется гармоническим анализом. Под практическим гармоническим анализом понимается представление конкретных функций, возникающих при решении практических задач, в виде ряда Фурье, коэффициенты которого, как правило, вычисляются приближенным образом. В большинстве случаев функции, описывающие исследуемый процесс, представлены экспериментальными данными или графиками. В подобных ситуациях коэффициенты Фурье вычисляются при помощи приближенных методов интегрирования.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Тригонометрический ряд Фурье. |
| Разложение в ряд Фурье периодических функций с периодом 2п. |
| Понятие дифференциального уравнения. |
| Простейшие дифференциальные уравнения первого порядка. |
