Определение. Многочленом (полиномом) от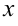 
называется функция вида:
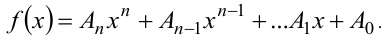
Здесь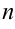 
— целое положительное число, 
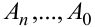— коэффициенты, действительные или комплексные. Число 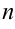называется степенью многочлена.
Корнем (нулем) многочлена называется такое значение 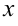, при котором он обращается в нуль.
Многочлен с действительными коэффициентами разлагается на множители с действительными коэффициентами первой и второй степени. Множители первой степени соответствуют действительным корням многочлена. Среди действительных корней могут быть кратные (одинаковые). Множители второй степени не имеют действительных корней, их дискриминант отрицательный. Множители второй степени также могут быть кратными.
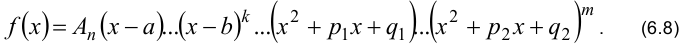
В записанном выражении (6.8)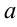 
— действительный простой корень, 
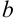— действительный корень кратности 
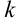, множител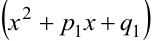и 
и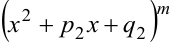 
не имеют действительных корней.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Интегрирование подстановкой |
| Интегрирование простейших рациональных дробей |
| Разложение рациональной дроби на сумму элементарных дробей |
| Интегралы от иррациональных функций |
