Разложение движения элементарного объема сплошной среды на поступательное, вращательное и деформационное (теорема Гельмгольца)

Разложение движения элементарного объема сплошной среды на поступательное, вращательное и деформационное (теорема Гельмгольца)

Разложение движения элементарного объема сплошной среды на поступательное, вращательное и деформационное (теорема Гельмгольца). Поле скоростей определяет характер изменения размеров и формы малого объема сплошной среды (жидкости) в процессе movement. As показано на рисунке. 3.11, при перемещении объема жидкости, ограниченного поверхностью A, отрезок ab через время D1 менял длину, поворачивался на определенный угол и принимал положение a’b*.Другие сегменты различаются по положению и длине. Вы будете Рассмотрим изменение положения, формы и размера объема сплошной среды за короткий промежуток времени. Поэтому подумайте, если вы хотите путешествовать на короткое расстояние.

При таком расстоянии изменение поля скоростей можно оценить по значению 1-й производной проекции скорости, предполагая, что вклад 2-й производной пренебрежимо мал. Людмила Фирмаль

• Из первых таких работ Вода из 3 составляющих скорости (каждая из них по 3 координатам (x, y, z), yy, yy|) будет равна 9.Прежде чем писать их, рассматривая поле определенной скалярной величины P (например, плотность Р, давление Р) колебаний φ вблизи фиксированной точки в пространстве характеризуется 3 производные φ для 3 координаты(ф/х/, д/, д/, ф/, ф/, ф/, ф/).Эти 3 производные считаются проекциями на соответствующие координатные оси и перемещаются в векторное поле величин ep, называемое скалярным градиентом： Поэтому, если вы знаете векторное поле полега3известно, вы можете вычислить, как скалярная характеристика EP изменяется вблизи любой точки в этом поле. Для анализа характера движения базового объема удобнее использовать Тензор ОГАСА! Этот тензор симметричен и Асимметричная часть и ее представление $ Тензор о симметричной части рептилии называется скоростью деформации Tensor.

It можно легко проверить, непосредственно вычисляя, что симметричная часть тензора 8 и асимметричная часть A определяются формулой. Вычислить тензоры$и A. Для удобства графических изображений мы предполагаем это явление в плоскости (xOy), то есть u2 = 0 и dich / dx = diu / dx = 0, с целью дальнейшего анализа движения и деформации определенного объема жидкости в пространстве. То есть рассмотрим плоское движение объема. Очевидно, что в этом случае только компоненты 3 и A внутри пунктирных прямоугольников (3.43) и (3.44) будут non-zero. In кроме того, в плоскости (xOy) для большей наглядности рассмотрим смещение и деформацию жидкости (сплошной среды), заключенной в первый момент в квадрат abcd (рис.3.12-3.15). Для упрощения анализа выберите декартову (x, y, z) движущуюся систему, скорость которой в точке a равна zero.

• В этом случае смещение и скорость точек, принадлежащих отрезкам-ab, bc, cd и hell относительно точки a, можно считать абсолютными. Заметим, что смещение (вращение) ребра aB в течение 6X относительно вершины a обусловлено изменением скорости u x вдоль оси Y. Производные, недиагональные компоненты тензора реберные кости будут адом. Подчеркните Сима Несимметричная часть Матрицы 3 и тензорный стержень, и、 Краевые перемещения ab и ab определяют компоненты тензора 3 и A в ячейках матрицы, соответствующих ячейкам матрицы качания. —And. So, да о^ АБ во рту происходит за счет ингредиентов И поверните туз! Комплектующие Тензор 3 и A соответственно. Дальнейшее упрощение последующего анализа с учетом несжимаемости fluid.

Рассмотрим вклад отдельных компонент тензора 8 и А В смещение во времени Д1 объема жидкости, ограниченного квадратом abcd. 1.Деформация растяжения-сжатия (линейная деформация).Диагональная составляющая тензора 3 сделана ненулевой、 0,> 0(рис. 3.12). в этом случае скорость всех точек на ребре bc Станьте позитивными и переместите дистанцию параллельно оси X. Ребро r движется в отрицательном направлении расстояние от оси Х-ас! 61, следовательно, наличие ненулевого Oh Zi и> 0 указывает, что квадрат abcd расширяется в направлении оси y и сжимается в направлении оси X.

В этом случае при различных смещениях ребер площадь квадрата, характеризующего объем жидкого элемента, остается постоянной. Людмила Фирмаль

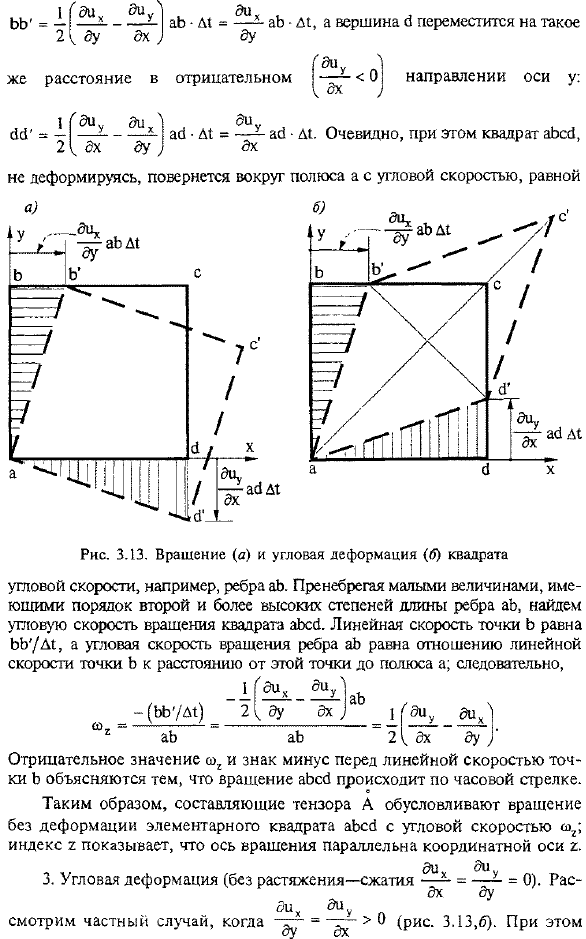
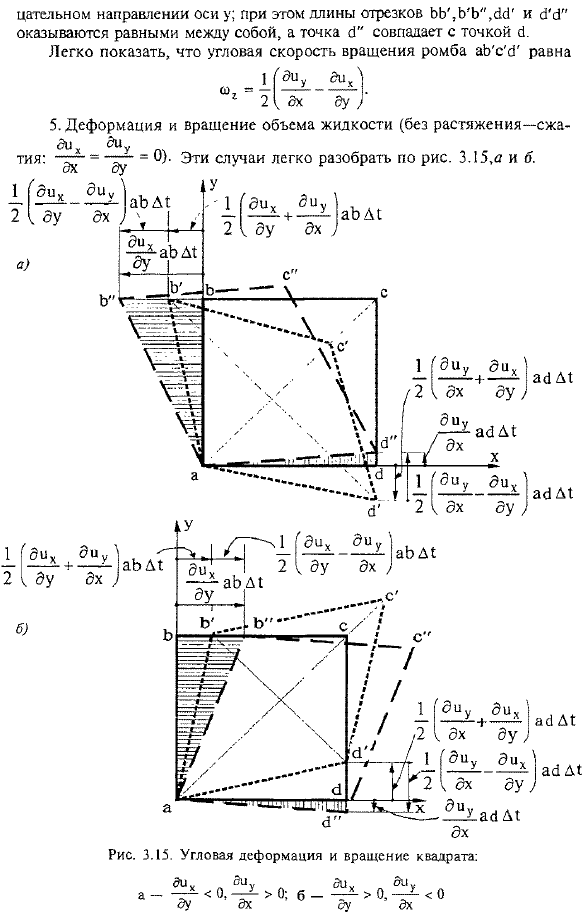
• Поэтому диагональная составляющая ３ вызывает изменение линейных размеров движущегося объема. 2.Вращение (вращение без натяжения, сжатия： Все компоненты тензора 5 равны Перемещение происходит только за счет недиагональной составляющей A (рис. 3.13). Топ-Коммерсантъ движется между D1 Положительный. > 0 x направление оси по расстоянию ab * D1 = ab * D1, и вершина a движется так Отрицательное же расстояние хо ’ Ай * Λ1—Ай-посетители Вращается вокруг полюса без деформации, но угловая скорость равна 0 направление оси y： Рисунок 3.13.Квадратный поворот (А) и угловая деформация(6） отрицательный знак перед отрицательным значением co2 и линейной скоростью точки b.

Смотрите также:

Примеры решения задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Гидромеханическая интерпретация теоремы Остроградского-Гаусса.
2. Векторная форма теоремы Остроградского-Гаусса.
3. Субстанциальная производная.
4. Потенциал скорости и функция тока при плоском безвихревом движении.