Оглавление:

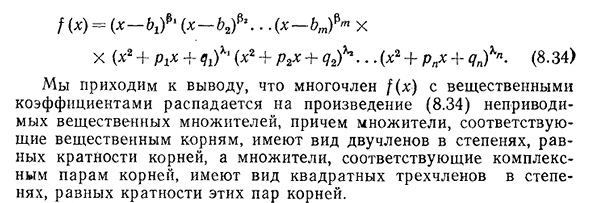

Разложение алгебраического многочлена с вещественными коэффициентами на произведение неприводимых множителей
- Факторизация алгебраических многочленов с вещественными коэффициентами в произведении неприводимых множителей. В
будущем нам придется иметь дело с многочленами от переменных, которые принимают значения E s e t l и W l как e s E S t e n s E.
Таким образом, эта переменная обозначается буквой X, а не З. Используя Людмила Фирмаль
теорему 8.3, находим разложение многочлена с вещественным коэффициентом f (x) в произведение неприводимого вещественного множителя. Многочлен f (x) состоит из множества pi, P2, Pm и корней
bi, b2, BT соответственно.\И AI A2 и A2, чтобы иметь комплексно сопряженную пару…L L2, соотношение AP и AP…, CP каждой пары соответственно. Тогда, согласно результатам п. 2, многочлен f (x)
- равен/(x)=(x-B^'(x-B ^ ‘ (X-B2? г.(X-HT)&t x x x(X-a^(x-a^{x-a2l(x-A2) 7’2. . .(ч—») СР (х-АП)^. (8.32) — корень AK (fe=l, 2,…. n) * через m и vk соответственно, т. е. пусть=+тогда AK=IK-ivk. Преобразуйте в любое & =1,2…, P выражение (x-AA)* * (x-ak)^=[(x-ak) (x-ak)]^=[(- uk-ivk) (x-u
k+wA)f== * [—uk) 2+v2k] * =(x2+p * x+qk)(8.33) где pk= — 2uk,qk=Uk v2k. В (8.33)используйте(8.32), чтобы разложить многочлен/(x) в произведение фактического неприводимого множителя: 312 Глава 8. Первичные и неопределенные интегралы /(x)=(x-b rf1(x-b2f2.. X(x2+Pxx4-f t/1 (x2+P2X+q2) K… (x2+R » x+<?4 (8.34) мы приходим
к выводу, что многочлен f (x) с вещественными коэффициентами распадается на произведение неприводимого целого числа (8.34, Людмила Фирмаль
Множители, соответствующие действительным корням, имеют вид степени интерактивности, равной кратности корней, а множители, соответствующие сложным парам корней, являются ступенями пары этих корней.
Смотрите также:

