Оглавление:

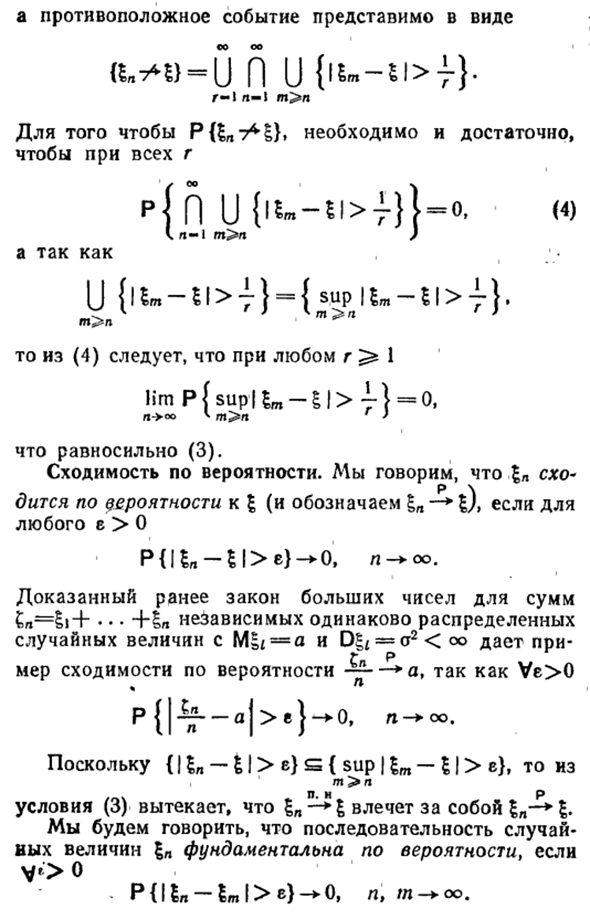



Различные виды сходимости случайных величин
- Сходимость различных типов случайных величин Почти определенная конвергенция. Последовательность почти наверняка сходится (Bp) Запись в случайную переменную, если P {Iim ln = l} = \, P-> OO Т.е. вероятность события {co: lim | i (<) Φ1 (<)) / 1-X » Равно нулю т-р бп Сходимость 1n-> I указывает на то, что каждый e> 0. lim P {co: sup Tm- £ 1> e} = »0. (3) p-> oo t> p
- Фактически, событие 1} может быть записано как 1 Oh Oh Oh u „->!} = n UП {lu-iK ^}, r-1 n- \ m ^ n Противоположное событие может быть выражено как 00 р-лрт-1 м> н Для PUrtT4 ^}, «Все г p {h U {lU- $ l> 7 -}} — 0 (4) I. n— 1 m> n) И так как U {l £ «» 6l> 7} ™ {sup ^ IU -SI> 7-}. м> н Тогда любое r> 1 из (4) lim P [sup I £ m-EI> m «} = 0, Это эквивалентно (3). Вероятность сходимости.
Скажем, вероятность сходится к k £ (и представляет ln►fc) P {ll „- | l> e} — * 0, A2 ° deg. Людмила Фирмаль
Ранее было доказано, что многочисленные законы независимы и одинаково распределены с суммой £ f «= £ i + ••• Mh — случайные величины с учетом a и Dh = a2 a, Ve> 0 p {| ¥ >> eb0 ‘ {| ln-11> e} s {sup | lm-11> e}, тогда м> л Условие (3) означает — ^ — l означает * Последовательность случайной величины В можно назвать основой вероятности. V> o Шπη — >> e} -> 0, n, m- + oo.
Для выполнения теоремы 2. Достаточно того, что последовательность является основой вероятности. р Доказательство. тогда из неравенства Означает основную {* „}. Для доказательства этого достаточно использовать следующую лемму. Лемма 2. Если последовательность является вероятностно базовой, то вы можете выбрать подпоследовательность, сходящуюся к a.s.
Доказательство. установите ii = 1 и определите nk как минимум N> ni по индукции, Для всех rt s ^ N 4 к Поэтому в лемме Бореля — Кантелли число событий, которые происходят с вероятностью 1, ограничено. о ~~ CI> «ЗГ # Поэтому ряд +] Г (Ц + | -Ц) будет сходиться L —I о Предполагая вероятность 1 и t = + 2-bpc) Получите g ^ fil ^ g, чтобы ряд сходился к нулю в оставшихся точках. Лемма доказана. Теорема 2 оказалась достаточной.
- Если вероятность является основной, то по лемме будет случайная величина ξ и подпоследовательность lnk, но в этом случае если-. »•» » P {I In -11> c) y} + P {Ib. Докажите еще один результат сходимости вероятности -5. Для теоремы 3.ξ функция распределения F \ n (x) слабо сходится к функции распределения F \ (x). Доказательство. Показывает событие {| £ л — 8} = An. о) от е / 1л
Тогда для любого х {| <* — in} = {£ i <} и Rn С каких пор P {$ < — e} -P (Jft) «e * Обратное верно, если F * (x) слабо сходится к вырожденному распределению. Теорема 4. 1n A c, если F \ и F \ вырождены в точке c. Доказательство. F \ n (c + e) 1 и Fin (c-e) -> 0, поэтому P {c-e <+ e} 1, -c |> e} — * 0, если необходимо.
Следующий пример показывает, что сходимость n сильнее вероятностной сходимости. Людмила Фирмаль
Пусть базовое пространство событий — это интервал Q = [Otl], событие — это борелевское множество, а вероятность — мера Лебега. Определите, если 2 * e> 0 P {I £ rt I> e} » Но в то же время 740} = 1. Средняя сходимость. В следующем случае говорят, что последовательность сходится со средним порядком r> 0. M | -i 0 0, n- * 0. (6) Когда r = 2, сходимость (b) называется средней сходимостью второго порядка.
Средняя сходимость порядка r определяется неравенством Чебышева. P {and— 11> e} <M | -‘G 8 Следуйте, что означает конвергенция Я Рисунок 13. Связь между различными типами случайной сходимости Количество. Таким образом, мы установили отношения между различными типами сходимости случайных величин (см. Рисунок 13).
Смотрите также:
Решение задач по математической статистике
Если вам потребуется заказать решение математической статистики вы всегда можете написать мне в whatsapp.

