Оглавление:




Расчёты балок конечной длины
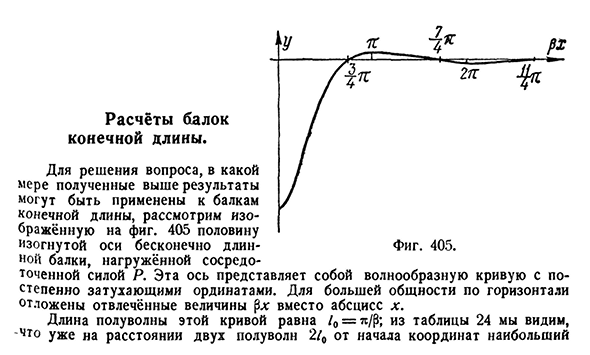
- Расчет конечной длины балки. волнообразная кривая- Рассмотрим, что показано на рисунке, чтобы решить вопрос, в какой степени приведенные выше результаты могут быть применены к балке конечной длины. 405 половина изогнутой оси бесконечно длинного луча-это сосредоточенная сила P. эта ось представляет собой сильно зависящие ординаты. Для увеличения общности горизонтальная ось
представляет абстрактное значение px с x-X. Длина полуволны этой кривой равна/0=te / P; из таблицы 24 видно, что она находится уже на расстоянии двух полуволн от начала наибольшего 2/0пучка на упругом основании[CH]. XXV Отклонение составляет^O только, 2°/o от отклонения под нагрузкой. Таким образом, практически отклонение равно нулю при x=2/0, а не x=OO.
Итак, полученную формулу можно смело использовать при расчете симметричной Людмила Фирмаль
балки длиной Z^4Z0, и если учесть, что отклонение No/0 составляет 4% от максимума, то балка Z^=2Z0 будет равна нулю. Для более короткого луча может быть применен метод последовательного приближения. Для этого нужно уметь вычислять M (x) и Q (x), когда бесконечно длинная балка нагружается с одного конца силой Около — \^T777777777777777777777777777777777777777777 И Фигура. 406. Пару Мес. Начало координат берется на нагруженном конце, а направление осей остается прежним(рис. 406). Начальным условием(25.4),
определяющим константы для выражения, является: 1) Когда x=Oo отклоняет y=0; следовательно, A=B=0; 2) когда d2v x=0 изгибающий момент M (x)= = EJ=3) x=0 боковая сила Q (x) Опустите промежуточный расчет. ~2^EJ’ И из третьего условия D=2EJ^ Тогда M (x)=-^~[Ro sin fix-MJ}(cosφ.Т+Син? х)]= — г[Ро-м м, (25.18)и Q (х) = — г-р[Ро (потому что исправить-грех Эд+2A4O8sin Эд=-[П^+2М^.].(25.19) весь прибор готов к расчету балки любой длины на упругом основании при интенсивных нагрузках. Рассмотрим пучок AB длины Z<2Z0, нагруженный концентрацией P на расстоянии от левого и от правого края B(рис. 407, а). Чтобы вычислить такой луч, замените его
- бесконечно длинным лучом(рис. 407, б). Для таких балок можно найти напряжение любого поперечного сечения, включая поперечное сечение DX и сечение, соответствующее кромке короткой балки. Таким образом, средняя часть A^B^(рис. 407, в) бесконечно длинная балка будет находиться под действием силы Р и силы на участке DX и по — § 155] расчет конечной длины 481 балки Направления усилий, показанные нами на чертежах B и Qa>Qb\, соответствуют их положительным значениям. Для того чтобы работа выбранной части балки AJ h совпала с работой данной балки AB, необходимо использовать сечение Ai: сила-Qa и пара-M a, а сечение B^-Q & I с
внешними силами. Таким образом, в первом приближении напряжение балки AB можно рассчитать как сумму напряжений в точках трех балок I и III сечений A^B^(рис. 407). Раздел 1П, П изгибающего момента и поперечной силы Для левой части знак y должен быть изменен на счет M «(x) и Q»(x) для второго луча, а для 406 эти формулы относятся к-правая часть луча I равна W=+jp-ребро Q i=. Поэтому, ЛГ’(х)=+р-1+г ВВ-з Но) И М»(х)= Для Третьего Луча следует поставить AG0=—и P0==+Qa., В) г)? м°\р щ а, З\4, л г»(л-) ф Н…? Одиннадцать. И » (Х)=-[ / — А————————— ( т. Стоимость
Пхи-g407. В сечениях А и в они численно равны изгибающему моменту и боковой силе этих сечений. Если в их расчетах используется Людмила Фирмаль
таблица 24, то необходимо изменить знак За счет поперечной силы сечения А. Таким образом, если вы используете таблицу 24 для расчета модификаций M»(x), M»(x), Q»(l) и Q»(x) и N p u, то дальний луч должен быть рассчитан из той же таблицы MA, и новые ошибки допускаются при расчете модификаций X=a и m, поэтому к сечению a l луча N и сечению B сила B не применяется. получается, но меньше, но равно нулю Расчет этой задачи был осуществлен многими советскими учеными, проводившими исследование упругого основания от академика А. Н. Н. Крылова до профессора А. Н. Крылова. П. Пузыревский, П. Л. Пастернак, В. В. Кречмер часть АСС ’ * д. Дутов,
профессор Н. К. Снитко, Б. Г. Коренев, В. А. Киселев, А. А. Уманский, С. С. Голушкевич, Л. В. Канторович, К. С. Завриев П. Ф. Папович Я. П Коробова с соавт. 482 Валки на эластичном основании[гл. XXV Разработан эффективный метод расчета (1923), который позволяет обойтись без описанного здесь метода последовательных приближений, он называется методом начальных параметров и отклоняется y (x).)、 Остальное легко получить дифференцированием, поэтому мы даем только уравнение y (x (25.20 )) Исследование изгибных балок, не подчиняющихся закону (25.20), проводили профессор Г. Е. Проктор, Н. м. Герсеванов, Я. А. Мачерет, Б. Н. Жемочкин, М. И. Горбунов-посадов, А. П. Филиппов, И. Г. Альперин, М. М. Филоненко-Бородич и другие
Смотрите также:
| Учёт массы упругой системы, испытывающей удар | Вычисление напряжений и деформаций. |
| Способ сравнения деформаций | Учет собственного веса и сил инерции |

