Оглавление:


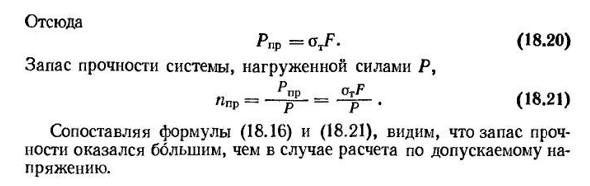

Расчеты при растяжении и сжатии
- Расчет на растяжение и сжатие Если растягивающие и сжимающие напряжения равномерно распределены по площади поперечного сечения стержня. В результате расчет прочности статической определяемой системы для допустимого напряжения и критического состояния дает те же результаты. Для статически
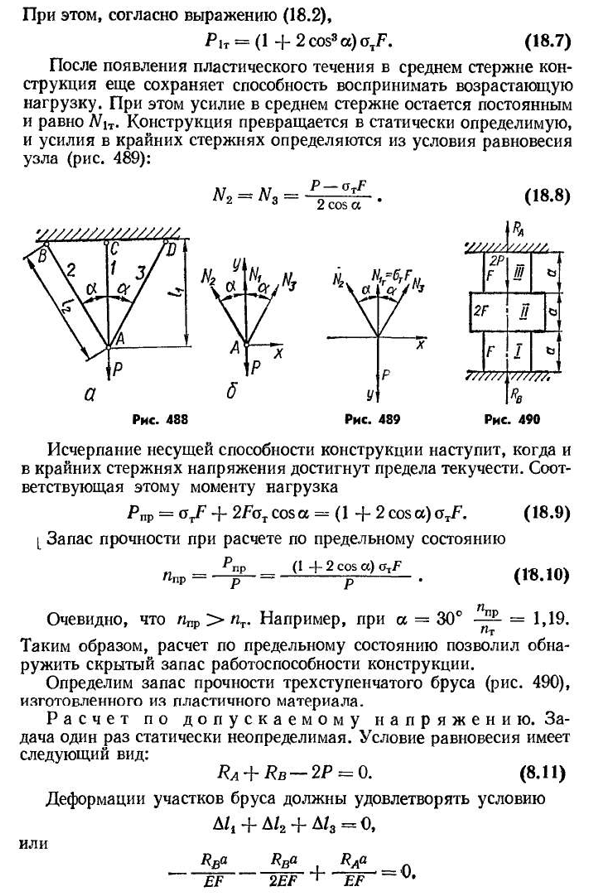
индетерминированных систем результаты вычислений различны. Давайте возьмем пример. Определяет запас прочности три-штанга подвески(рис. Нагруженный с усилием R 488, a), площадь поперечного сечения стержня одинакова.
Материал имеет предел текучести из пластика. Применение за-дача ’ один раз статически Людмила Фирмаль
неопределимо. Его решение рассматривается в статье 37. Когда FT-F2 коэффициенты k=I и далее из уравнений(5.50)и(5.51) получаем — 4-2С Ф р р’ Н2=Н3=а * К1-Ф-2cos3a П. (18.2) (18.3) Очевидно, что всегда L>LG2=M3, т. е. большая сила возникает в среднем полюсе. Таким образом, центральный стержень будет иметь самое высокое напряжение: Л’1 1Р з ф О Р»1_|2cos3A Ф • Запас прочности при расчете допустимого напряжения (1 4-2cos3a) F A T п (18.5) Это позволяет
повысить производительность вашего приложения. Конечное состояние конструкции характеризуется истощением несущей способности, которое происходит, когда стержень со всеми напряжениями достигает предела текучести. Найдите предельную нагрузку на конструкцию. Поскольку напряжение в стержне во время упругой операции неравномерно (в промежуточном стержне, чем в крайнем случае), напряжение текучести не достигается
- одновременно на всех стержнях. Во-первых, под нагрузкой P1t пластическая деформация происходит в среднем полюсе. Усилия в этом направлении ЛД-г-OjF•(18.6) 490 при этом, согласно формуле (18.2), P1T=(1+2cos3a) o TF. (18.7) после появления пластического течения в среднем полюсе конструкция все еще сохраняет способность воспринимать возрастающие нагрузки. В этом случае, мощность центрального стержня остается постоянной и равна # его. Структура становится статически определимой, и сила крайнего стержня определяется из состояния равновесия узла (рис. Четыреста восемьдесят девять): П-gTF2cos в * Рис четыреста
восемьдесят девять (18.8) У/ / / / / » Uhul… 2Р F W 2Ф Ч<Ш F I b 77/77 7/7 ///, * В Рис четыреста девяносто Истощение несущей способности конструкции произойдет, когда напряжение на крайнем стержне достигнет предела текучести. Соответствующая нагрузка P PR=gtF+2FaT cos a=(1+2cos a) oTF. (18.9) L запас прочности для предельных предельных состояний (1 4-2cos a) (18.10)) Понятно, что в Ипре>например, −30°-1,19. Таким образом, расчет предельного состояния позволил выявить скрытые резервы
эффективности конструкции. Определите запас прочности трехступенчатой балки (рис. 490) изготовлен из пластика. Людмила Фирмаль
Р а с Ч Е Т О Д О П У С А М О М у Н А П Р и Ф Е Н И я. задача не раз определялась статически. Равновесное состояние выглядит следующим образом: Ra+Rb-2P=0. (8.11)деформация поперечного сечения стержня должна соответствовать условию D/(4-D / 2 4-D / 3=O), Или РБА РБА/РБА д EF2EF+ее-в’ -И из этого следует, что РА=^ — р б.(18.12) Подставляя значение RA в выражение (18.11), можно увидеть следующее Rb Реакция верхней фиксации Ile=4-р. (18.13) (18.14) Четыре. Секция / и II балки сжимается силой Nj-MC — — — ^P, а секция III растягивается силой N m — ^P. Максимальное напряжение возникает в верхнем поперечном сечении. Это напряжение Ojij-nii&п ф-5Ф (18.15)) Запас прочности по пределу текучести Из 5o^Ф P t~ ~ ^g~ ~ V~R’(18.16) R A C h e t p o p R e d e n o m u s S o S t o I n i u. во-первых, давайте посмотрим, каково предельное состояние рассматриваемой
системы. Из приведенных расчетов следует, что она находится в диапазоне упругости l/>O/>O//. Таким образом, при увеличении нагрузки предел текучести сначала достигает верхней части. Это состояние не приводит к истощению несущей способности системы, так как нижняя секция, находящаяся в упругом состоянии, сопротивляется повышенной нагрузке. Сила, которая воспринимается верхней частью, при этом всегда: NFP= = OTF. (18.17) Фаза I и II сжимаются силой УУ/= = р б=2Р-Ра-2Р-О. Ф(18.18) При дальнейшем увеличении нагрузки пластическое состояние возникает в нижней секции, напряжение больше, чем в секции II, промежуточная секция между областями пластической деформации увеличивает
сопротивление движению. Таким образом, предельное состояние системы характеризуется появлением текучести одновременно в верхнем и Нижнем сечениях. Предельная нагрузка определяется из условий Но _ ЗНП__з пр т U/НР-ф » ф — О Дж.(18.19). HRD-OjF Запас прочности для систем С усилием R, п — Что? PR-RT UK Р-Р-Р-Р-Р-Р-Р-Р-Р-Р-Р-Р-Р-Р * (18.20 )) (18.21) Сравнивая формулы (18.16) и(18.21), можно видеть, что запас прочности больше, чем при расчете допустимого напряжения.
Смотрите также:

