Оглавление:







Расчет вращающихся дисков
- Расчет вращающегося диска Вращающийся диск широко используется в паровых и газовых турбинах, компрессорах, вентиляторах и машинах в химической промышленности. Диск подвергается воздействию нагрузок, которые растягиваются или изгибаются, а также высоких температур. Центробежная сила необходима. Как правило, поля нагрузки и температуры симметричны относительно оси диска, а напряжение является
функцией только расстояния от оси вращения. Мы попытаемся ограничиться рассмотрением диска определенной толщины, нагруженного силой, параллельной его центральной плоскости и равномерно распределенной по его толщине, а также рассмотрим нагрев диска по линейному закону изменения температуры вдоль радиуса. Будем считать, что диск тонкий, не изменяется в результате этого напряжения на его толщину и не существует в
направлении, параллельном оси (og=0). В этой постановке задача определения Людмила Фирмаль
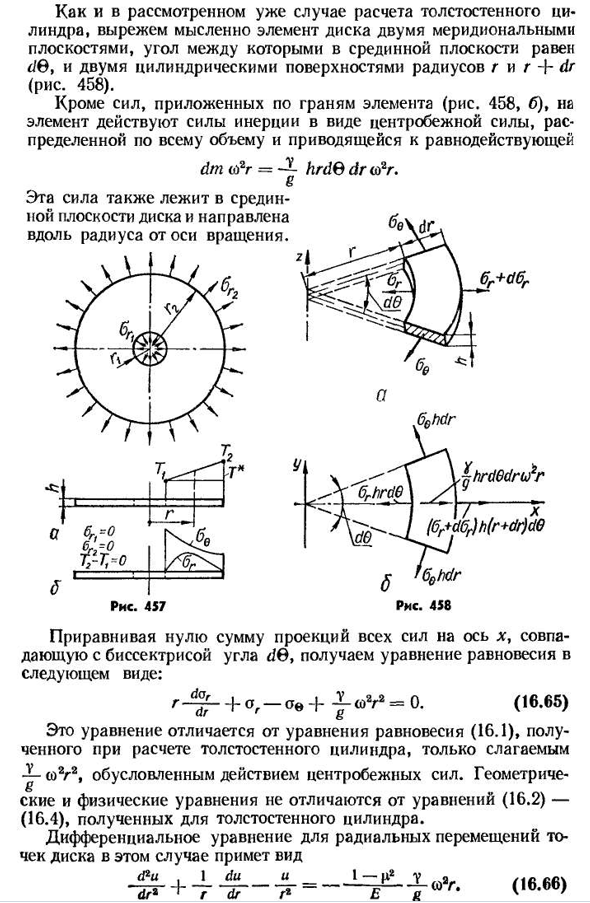
напряжений в диске относится к так называемой плоской задаче теории упругости, то есть задаче о плоском напряженном состоянии. Рассмотрим вращающийся диск определенной толщины/г с центральным отверстием(рис. 457, а). Кроме обозначения фигуры, возьмем следующее: Y-удельный вес материала диска; И если вы интегрируете его дважды подряд с = + ©2А(16.68) Введение этого решения в уравнение для напряжения (16.4) дает следующее уравнение ОГА==а+4—Т-«(16-6) ) 8г (16.70) Куда? A=4,A B= — — — — —
константы BP A и B (следовательно, A) и BJ определяются из граничных условий. Наиболее известны радиальные напряжения на наружном и внутреннем контурах диска. Тогда g-VG — =og1, а g=G2AG = OGG. Согласно выражению (16.69), эти условия дают два выражения: Ноль. «=л+ — ^ — А±В4.л;; О G. — A+B .2 2. 8 8 8 3+П-В fn2r2G2 8Т Вт R2 решена в отношении б, с G2a ««я с-О Г,—— , 1, + G2h Г2-ч р» г ’ Г2 «Г2-G2Gft Г2-Г2°г’ 8£ч? Если отсутствует внешняя и внутренняя цепи диска напряжения G1g2H y, т. е. SGG=0 и=0, то В-(16.74) Подставляя последние значения A и B в выражения (16.69)и (16.70),
- получаем l [(З+П)0+4+^ К +(16.71) (16.72) (16.73)) (16.75) а » =4-Ф®2. (16.76)) 461полагая для краткости 1+3 / H. 3+R (16.77)) Формулы(16.75) и (16.76) могут быть записаны как og-C[1-M2 (1—P2];o«=C[1+k2 (1 4—mp2]). (16.78) (16.79) Напряжение og положительное и, как легко видеть, достигает своего максимального значения при p=V-k=тогда (Og)max=C (1-L)2. (16.80)напряжение ov при всех значениях p также положительно, достигая наибольшего значения на внутренней кромке диска (p=k): (®e) max~S[2+(l-m) k2]. Сравнивая формулы(16.81) (16.80) и (16.81), убедитесь, что (OE)max всегда больше (og) max. Поэтому при проверке прочности диска в соответствии с энергетической теорией изменения формы условие прочности
следует записать в виде Osbbiv — (OO) max-C/2 (1— / I) k2][o [(16.82) в случае хрупких материалов испытание следует проводить по теории Мора, а в случае O3-0-og 82 по той же формуле (16). Характер распределения напряжений от радиуса диска с отверстиями K=0,2 и p-0,3 показан на рисунке. 457, б. Формула для напряжения твердого диска (без отверстий) может быть найдена из уравнений (16.69) и (16.70), в оси диска (g—0) напряжение должно иметь конечное значение, для того чтобы удовлетворить этому условию, константа B должна быть равна нулю.: = (16.83) О — =А-Ш Н. ^2. (16.84)найти константу A из граничного условия на внешнем контуре (в g-G2).
Если диск подвергается воздействию только инерционных сил Людмила Фирмаль
собственной массы, вызванных вращением, и во внешнем контуре отсутствует внешняя нагрузка, т. е. ОГА-0, то формула(16.83), А=<ОЧ(16.85) 463поставляя значение этого выражения A (16.83) и(16.84), которое имеет приблизительно>=with(1-P2); (16.86) A0=with(1-/PR2). (16.87)оба напряжения положительны для всех значений p и увеличиваются по мере приближения к оси диска. На оси диска, легко определить смещение и деформацию диска от давления найденного в p-O (<СТГ-1xae)+А Г ; т. (16.92) Что= — гр(0Е-Р-ОЖ — | — в. И если мы решим эти уравнения вместе、 г=•г » ПГ Тер+РЗЭ — (1 4-с) А71; (16.93)) o » =1 1ee+—(1+и) 464читывая формулы(16.2) и (16.3), имеем г г И. Г (16.94) Ов=-Т^Г-[^+С-^-(1+я) » т]. T=T2-7(См. Рис. 457, а). С изменением температуры линейным вдоль радиуса диска T-T*—~G1, etc.- G3G1 Форма этих выражений «=tchg [- г-+п-г-(|+н) » г -^]: (‘М5>
(16.96) Предполагается, что модуль упругости и коэффициент Пуассона постоянны, не зависят от температуры и равны этим значениям при средней температуре диска. Подставляя уравнения(16.95) и (16.96)в уравнение равновесия (16.91), получаем следующее дифференциальное уравнение для определения смещения температурной задачи:, 1_ _ L. 1+и y * dr*+g dr g * ~G2-g/l (16.97) (16.98) Затем закрепите его дважды последовательно и мы получим решение для перемещения: С-CfT4— + 1 +м3(гг — <я) Т * А (£16.99)) Подставляя это решение для формул напряжений (16.95)и(16.96), получим (16.100) (16.101) Куда? g>D2T— Константы C и D можно определить
из граничных условий: g=g в\OG напряжении,-0g-OG напряжении в gg=0. Если вращающийся диск нагревается неравномерно, то давление от давления центробежной силы и температуры следует суммировать. При линейном изменении температуры 46sradius, добавьте правую часть формулы(16.69)и(16.100), а также Формулы(16.70)и(16.101), которые мы имеем. K+ «V -» Eg (16.102) «b-K-4-C — t A e E g’ <|s -, (13>где K=A+C, L=B+D-новая константа, которая также определяется из граничного условия. Пример 73. Определите вращение определенной толщины с центральным отверстием и напряжения в неравномерно нагретом диске. Наружный диаметр
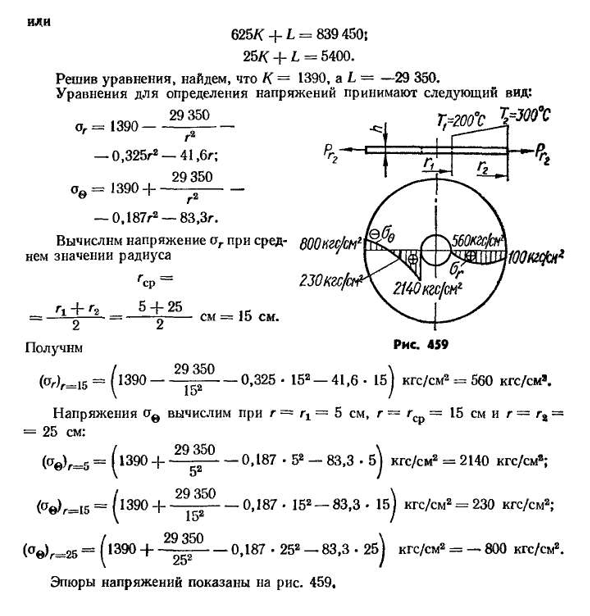
500 мм, Внутренний диаметр −100 мм, толщина диска и число оборотов на единицу длины наружного контура диска n=3000 мм, наружный контур диска RG*=100 и внутренний контур RG=100=температура внутреннего контура 71=200°С, а наружные изменения вдоль материала диска — £ =2 * 10E килограммов/см2 стали; p,=0,3; u=7,85•10 «3kgs/cm8»; a=125•10-7. Рассчитаем суммарные напряжения, вызванные центробежной силой и неравномерным нагревом. Для этого используйте формулы (16.102) и (16.103). Попробуем вычислить значения, содержащиеся в этих формулах: Подставляя эти значения в выражения (16.102)и (16.103), получаем следующее выражение З+н в СО2=• 3,3 0,00785 1 3,14 ■
3000U8 8 981\30 1 1+3^1y6V2—- 1,9 0,00785 ( 3,14 • 3000 \ 8 8 981 30 ) Тонны* — И что же?»»=» Сто. 125•10-7. 2. Один. 3(Г2-Г1)3(25-5) 2г * £2 = 100 125 ю-7 ″ 2.Один. Файлы 3g2-В3 25-5 Л ИГ==с+—0, 325g2-41.6 г; Г2 Л =К — — — 0, 187г2-83,3 г. Константы K и L найдены из граничных условий: g=q=5см ОГА=о ф с j=0; g=G2=25 см РГ, 100 Q Р =Gf= — T5 — — — кгс / см2=100 кгс / см2. h I эти условия дают следующие два уравнения: 1″»’ Я Я Или 625/(+L=839); 25 / < + L=5400. б Решая уравнение, находим K-1390, L-29 350. Уравнения для определения напряжений принимают вид: 29 350. ОГА=1390 — Г2 −0, 325т2-41,6 г;29 350 И в =1 3 9 0 + —— — — 0, 187т2-83,3 г. Вычислите напряжение IG со средним значением радиуса В
Смотрите также:
| Температурные напряжения в толстостенных цилиндрах | Элементы теории тонкостенных оболочек Введение |
| Примеры расчетов толстостенных цилиндров | Напряжения в осесимметричной оболочке |

