Оглавление:



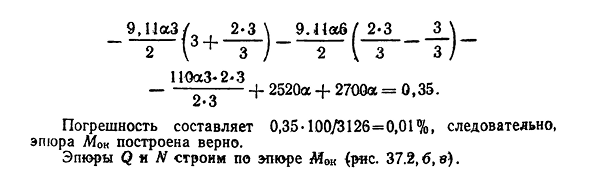

Расчет рамы на тепловое воздействие
- Расчет каркаса на тепловое воздействие, помимо силовой нагрузки от собственного веса, веса технического оборудования, снега и др. В статически определимых системах коэффициент внутренней силы не
возникает из-за теплового воздействия, а только деформация системы происходит из-за удлинения и кривизны осей стержня,а в статически неопределимых системах возникновение деформации из-за тепловых эффектов предотвращается чрезмерной связью, и в этих системах возникают внутренние силы.
При определении внутренней Людмила Фирмаль
силы в статической неопределенной системе от теплового воздействия методом силы начальный этап расчета аналогичен расчету внешней нагрузки:в данной системе эта разность появляется в нормальном уравнении. Смещение нагрузки главной системы заменено смещением ДД, 447ванными тепловыми ударами в
направлении отбрасываемых избыточных связей. Например, для системы дважды статически неопределенной канонические уравнения при расчете теплового эффекта записываются следующим образом: 4 * ^12 4″^lt=0;1^21X f4 — ^22 4 » &2t-0J Так как каждое каноническое уравнение запрещено в данной системе в этом направлении, то из действия всех неизвестных Xj и тепловых
- эффектов можно получить падение в основной системе. Движение Ajt (свободного члена) определяется формулой Максвелла-Мора Где Mj-график изгибающего момента в первичной системе от силы Xj=l; a—коэффициент линейного растяжения материала;/Vj-мощность XJ=L-коэффициент линейного растяжения в первичной системе. Так как отсутствует фигура изгибающего момента вследствие теплового воздействия основной системы, то конечная фигура изгибающего момента данной системы определяется найденным значением неизвестного. МОК=Ml Xi+M2X2. Универсальный кинематический
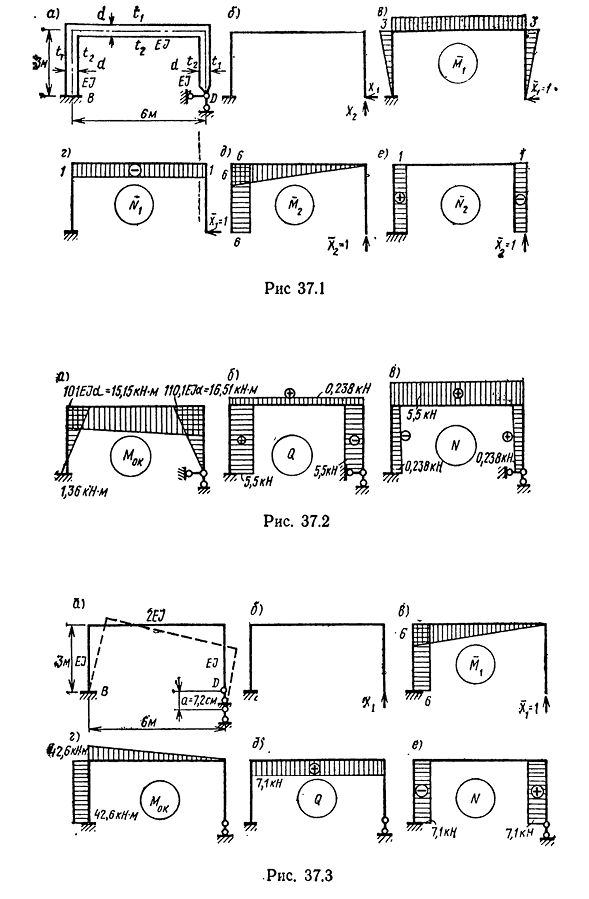
тест эпюры конечного изгибающего момента показывает совместное действие силы xj и направления падения связи от теплового воздействия, которое должно быть равно нулю.: МОК MD ds EJ Графики Q и N строятся таким же образом, как и расчет внешних нагрузок. Например. Участок M, Q, N в кадре(рис. 37.1, а), наружные волокна стержня нагреваются до/1=50°С, внутренние волокна нагреваются до/2=10 ° С,£7=15мн-м2, a=10-5 и высота поперечного сечения всех стержней d=0,4 м., 448,2 37,1 б) Рис 37,2 Л б) М’ Рис 37.3 решения. Степень статической неопределенности данного кадра равна: L=Cqn+W-ZD= 5 + 0 -3 1 =2. Опустите опорный
стержень в опору D и выберите основную систему. 37.1, 6). Запишите Людмила Фирмаль
каноническое уравнение: ^11 + ^12 %2 + = 0″ 1 ^21 4″ ^12 %2 + &2t=0. }Force Xi=L и X i=l при непрерывном нагружении основной системы она создает график изгибающего момента Mi и M2 и график вертикальной силы L^2. 37.1, 8). Рассчитаем коэффициент неизвестности для решения с учетом только изгибающего момента: =V G 45_,__. — — EJ=2-3£V+EJ+2 3, 3, 6, 3, 6, 3, 6, 3 3-3-2 3 3 3-6-3 2. 6-3-6 6-6-2 6 180 Эдж’ Вычислить свободные члены канонических уравнений Di=(50-10)AZ-Z0, 4-2 (50-10)АЗ-6 0,4 (50-10)AZ-Z-0.4-2 + (5 0+10) AB- — ——-= 2520а;2 д (50-10)A6-3 (50-10)A6’3 , (5 0 + 1 0 )А Z0,4 0,4-2 + 3 0,4-2 (5 0+10) AZ= — 2700A. Два. Подставляя полученные значения коэффициентов для неизвестных и свободных членов в нормальное уравнение,
получаем 72xx-81X2+2520-7a=0; 1-81Xj+18X2-2700EJa=0.J когда мы решаем это уравнение, мы находим X i=-36, 7EJa и x2==-15,19 EJa. Найденные отрицательные значения сил Xi и x2 указывают на то, что их действительное направление противоположно первоначально принятому направлению. Создайте окончательный график изгибающего момента(рис. 37.2, а). МОК=Mi Xi+m X2. . Мы делаем универсальную кинематическую экспертизу построенного МОК <b+d+ , Фаза A2t= — r “ 4509 ,121 0 3(/ 3 + 23-3 \ / 29 .N(a B3 / 2-3Z3 \/ Номер 110.-2-3 — — ——+ 2520a+2700A=0,3 5. Л’о. Ошибка составляет 0,35*100/3126=0,01%, поэтому график МОК построен правильно. Участок Q n n построить на участке МОК{рис. 37.2, б).
Смотрите также:
Примеры решения задач технической механике
| Статический способ построения линий влияния в однопролетной балке с консолями | Кинематический способ построения линий влияния |
| Прогибы при косом изгибе | Линии влияния при узловой передаче нагрузки |
Если вам потребуется помощь по технической механике вы всегда можете написать мне в whatsapp.

