Оглавление:











Расчет балок переменного сечения на прочность и жесткость
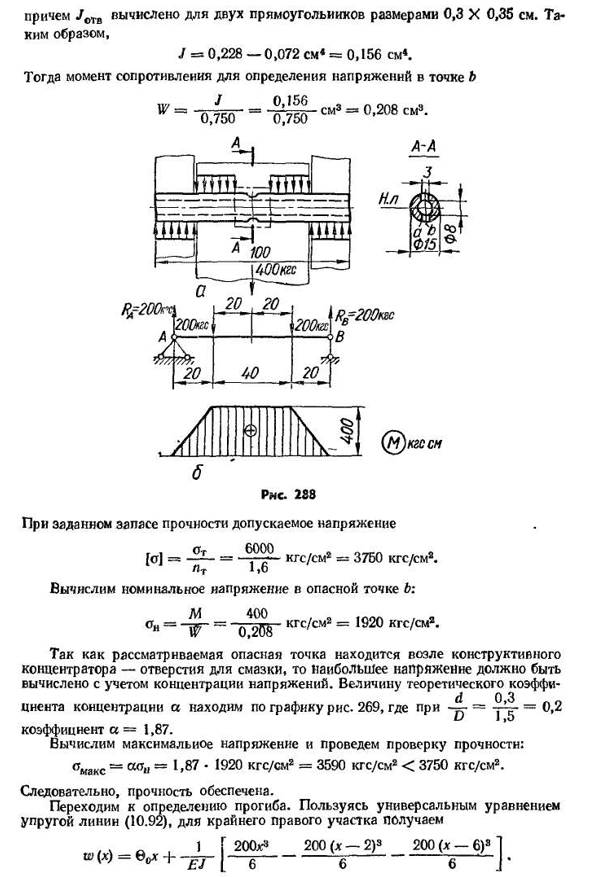
- Расчет балок переменного сечения на прочность и жесткость До сих пор расчет изгибного стержня учитывался, но деталь оставалась постоянной под давлением. Такие стержни, особенно при их значительной длине, нельзя считать разумными с точки зрения веса, и далее, по конструктивным причинам, изгибающиеся стержни, такие как размеры секций, часто имеют конусность, отверстия, углубления, неровности и т. д. По этим причинам на практике широко распространены стержни нефиксированной длины сечений. С точки зрения расчета прочности и жесткости все такие стержни можно разделить на три основные группы: а) сечение 287, которое
имеет локальное изменение в виде а) сечения а) ступени а) стержня переменного сечения (фиг. В) размер непрерывно изменяется по длине и поперечному сечению стержня(иногда фасонного) (рис. 287, в). И размер 287, b): 295º существует множество деталей, сочетающих в себе различные виды нарушения размеров и формы поперечного сечения. В этом случае при расчете прочности и жесткости необходимо учитывать все особенности, присущие тому или иному виду нарушения формы и размеров. Перейдем к рассмотрению каждой группы в отдельности. Локальные изменения формы и размера сечения
. Другие нарушения формы и размеров отверстий, углублений и сечений вызывают резкие и значительные Людмила Фирмаль
изменения в характере распределения напряжений и деформаций. Однако это возмущение носит локальный характер, и напряженно-деформированное состояние стержня в целом влияет незначительно. Поэтому определение прогиба и угла поворота секций, отверстий и других нарушений не рассматривается. При расчете прочности тангенциальные напряжения не учитываются, и основным условием прочности является то, что концентрация напряжений (§ 65) является одним из ослабленных участков, как это может быть. В зависимости от чувствительности материала к условиям концентрации прочности, т. е. он будет иметь различные формы: высокую пластичность материалов (низкоуглеродистая сталь, медь, алюминий) и хрупкость.: (10.129) Для однородных хрупких материалов(высокопрочная закаленная сталь) (10.130) Здесь а-
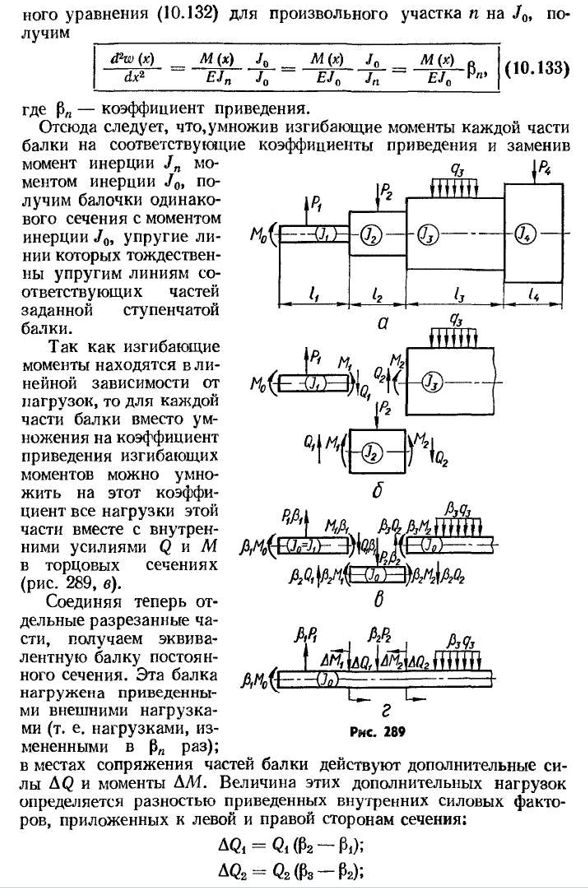
теоретический коэффициент концентрации, который определяется справочной таблицей (§ 65). В обеих формулах W-момент сопротивления ослабленной части. Пример 45, штифт (неподвижная ось), изготовленный из легированной стали 20x (- 60KGE/mm2), имеет размеры, показанные на рисунке. Он нагружен с усилием 288, a, и 400 килограммов. В центре пальца имеется отверстие диаметром 3 мм для смазки. Необходимо проверить прочность, если коэффициент запаса прочности PT = 1,6, и найти прогиб посередине. График расчетной схемы и изгибающего момента пальцев показан на рисунке. 288,6. Опасно будет ослабленное поперечное сечение, см. м-400кгф•. Опасной точкой будет, строго говоря, точка а(рис. 288, Об), но для расчета удобнее принять в качестве опасного условия пункт 6,
- что, очевидно, не совсем вводит в заблуждение расчеты. 1 момент инерции ослабленного участка — ^БР^ОТВ» Куда? ’■* — -* ^4 ′ — «• — „да. =2[—+° 0Л’3 5′ ° ’5 7 5 2 ] см< = °’ 0 7 2С м*’ 296prichem j OTB рассчитывается для двух прямоугольников размером 0. 3X0. 35 см, J=0,228-0,07 СМ4 = 0. 156cm4. Затем момент сопротивления определяют по напряжению точки в При заданном запасе прочности допустимое напряжение Шесть тысяч. 1.6 Кг / см2 3750 кг / см2. Рассчитайте номинальное напряжение в точке риска B: M400 кгс / см2=1920 кгс / см2. Максимальное напряжение должно быть рассчитано с учетом концентрации напряжений, так как опасная точка задачи находится вблизи структурного концентратора (смазочного отверстия). Кстати, значение теоретического коэффициента концентрации а показано на графической диаграмме. 269, где~= — p t=0,2 Коэффициент а=1,87. Рассчитайте максимальное напряжение и проверьте прочность:
ом AKS-AON=1.87 * 1920kgf/cm2=3590kgf / cm2<3750kgf / cm2. В результате обеспечивается прочность. Перейдем к определению отклонения. Используя универсальное уравнение упругой линии (10.92), найдите наиболее правильный участок следующим образом Вт= ! 2003 200 (x-2)3 200 (x-6)8 1 6 6 Учитывая условие, что отклонение 297правой опоры (x=8 см) равно нулю, получим выражение, определяющее начальные параметры• * 8+(8s-6“-23)=O, И так оно и есть. Ноль. — J2 0L Теперь получим формулу для определения прогиба середины пролета Здесь при E=2,0 * 10E кгс / см2 и J J6p-0, 228cm4 мы находим его в (4)=Ф=В0-4 + — ох<43-23), = = −0.0064 см, G L PEL/O » 0 6 4I / =0,064 мм и-= То есть Шаг Штанги. Концентрации напряжений возникают на стыке участков с различными размерами поперечного сечения.
Если материал чувствителен к нему, то необходимо применить условия прочности (10.130) ко всем участкам, которые находятся на границе участка. Людмила Фирмаль
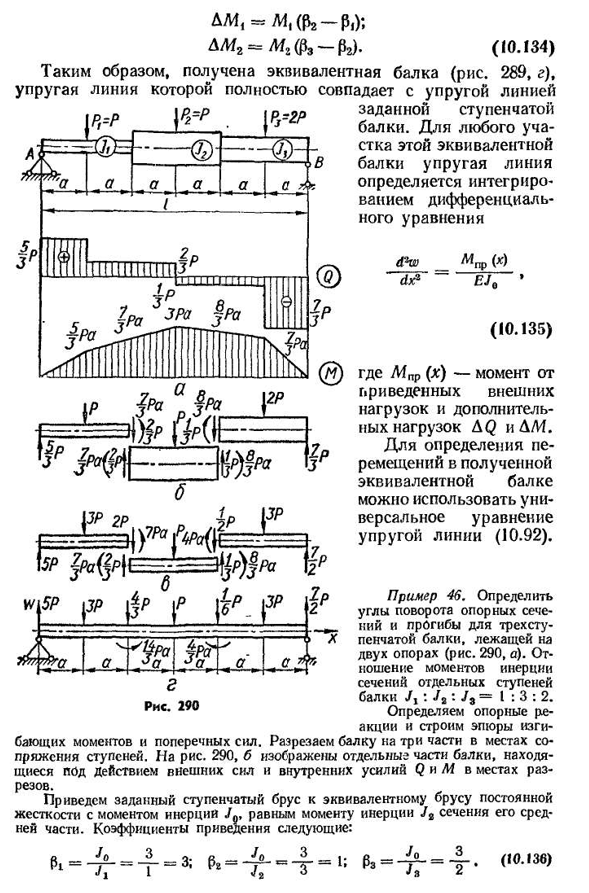
Если материал нечувствителен к концентрациям напряжений, необходимо добавить несколько вероятных опасных участков к условиям прочности(10.129). Для определения перемещения ступенчатого стержня используют общий метод, описанный ниже(Глава 13), или метод коррекции исходных параметров. Суть последнего заключается в замене ступенчатого стержня стержнем равной, постоянной жесткости в плане деформации. Рассмотрим обоснование такой замены на примере произвольной многолучевой системы (рис. 289, а). Разделите балку на части определенного поперечного сечения(рис. 289, Б), приложенный для расположения разреза, соответствующий внутренний коэффициент мощности-Q и M. Дифференциальное уравнение упругой линии первой части принимает вид d-w (x) M(x) g a% 2-p jt * <а также все последующие
призменные части d2w(x) M (x). #д? w (x) M (x)dx * ~EJt» * * * ’ dx * ~EJn•(10.132)умножает заданную ступенчатую балку с числителем на правой стороне последнего дифференциала и знаменателем на эквивалентной балке определенного сечения с моментом инерции (Jo), равным моменту инерции одного из сечений балки- 298 уравнения (10.132)для любого участка n/0, мы учим l к ___________________________ _ d2W (к)М (х)М (к)м (х)р dx2 «EJn Jo-EJn „7 7“ * EFA/P » >(lU. ДВ ) Отчет Где RL-коэффициент уменьшения. Поэтому изгибающий момент каждой части балки умножают на соответствующий коэффициент уменьшения, а момент инерции Jn заменяют моментом инерции Jo для получения балки того же сечения на момент инерции Jo. Поскольку изгибающий момент линейно
зависит от нагрузки, для каждой части балки, вместо умножения коэффициента уменьшения изгибающего момента, всю нагрузку этой части в конце 289). Если соединить здесь отдельные режущие части, то получится эквивалентная балка определенного сечения. Этот луч нагружен с уменьшенной внешней нагрузкой(т. е. нагрузкой меняя временами); дополнительная сила aq и когда AL4 действует на соединении компонентов луча. Величина этих дополнительных нагрузок определяется разностью приведенных внутренних коэффициентов мощности, приложенных к левой и правой сторонам сечения; AQi=Qi (P2-DSG-0,2).(); Это даст вам
эквивалентный пучок фиг. Его упругая линия идеально совпадает с упругой линией данной ступенчатой балки. Для любой части этого эквивалентного пучка упругая линия определяется интегрированием дифференциального уравнения д * ш м(х) (10.135) Где M PR (x) — момент от внешней нагрузки и дополнительной нагрузки AQ и DM уменьшаются. Уравнение универсальной упругой линии(10.92)может быть использовано для определения эквивалентного полученного смещения балки. ;= г г Но jPa-за. Но * Пример 46. Определяет угол поворота опоры и прогиб трехступенчатой балки на двух опорах(рис. 290, а). Соотношение моментов инерции секций отдельных ступеней балки а: и:3: 2. Определяли реакцию опоры и строили график изгибающего момента и поперечной силы. Разрежьте балку на три части на стыке ступеней. Для риса. На рис. 290, б
показаны отдельные части балки, находящиеся под действием внешних сил и внутренних сил Q и M. В месте разреза. Jo3l мы вычитаем данную ступенчатую балку из эквивалентной балки постоянной жесткости с моментом инерции L, равным моменту инерции J2 ее центрального сечения.≤2_Jo_3_p_Jo_3″/ / 22 3″л’ ≤3~С2(10.136) Умножьте нагрузку, заданную для всех секций, на коэффициент уменьшения$n, который соответствует Q и M секции секции. Все три части применяются к указанной нагрузке. 290, V. Теперь сделаем их в один стержень постоянной жесткости E JQ= » £J2, AQX для приложения дополнительных сил к секции использования, AQ2 и дополнительного момента Al! X и DL12. Вычислить дополнительные дроби AQ1= — / — P-2P= — — — — / — P, или DF,= -| — P(1 — 3) = —- | — П; Вычислите дополнительные моменты: DLI,=2-RA-7ra= — — — RA, или DLI,=2-RA(1-3)= — RA,&Mg=4ra— — | — / — RA=2. p a, или DL12=~RA (- |—— 1 j= — RA. Указывает нагрузку, приложенную эквивалентной балкой. 290, g. To убедитесь в правильности расчета эквивалентной нагрузки на балку,
проверьте, соблюдено ли условие ее равновесия:£L4 (/)=Zra+2-P•2ya+Za+2-P+4A — — П-п»+4Р»-(я т-21Т) п» — Перейдем к определению смещения, используя метод начальных параметров. Возьмите крайний правый участок и напишите для него уравнение упругой линии: w (/x)=W. o I1G14p(x-2A)2 4p (x-4A)2. о+ [- — — — — — — — Р А — — — — — — + — Ра——- 4 4- 5P2L_CR_4p(x-2°) 3_p(x- 3 °)3 + 5 / 6 3 / 6 3 P6 1 6 l, за п<х-W_WR(х-м3 1 6, 6, 6. (10.137) Начальный параметр определяется из опорного условия, если x-0w (0)=0, следовательно&’0=0;/ — 6A Gy (G)=0. Используйте это условие для определения второго начального параметра B0: Откуда 0о= — 10.58 Р -. (Да. 138) для определения угла поворота правого конца балки дифференцируем уравнение упругой линии самой правой части балки (10.137) (5AR(6А-З) 3 2 2 3 2 Р (6а-4а) «ОГ>(БА-5А) с]6′ 2 Вт R2J Где его найти » R® Е Ят’ (фо. Сто тридцать девять.) Например, прогиб в месте приложения внешних нагрузок P j и P2 (т. е. сечений x-a и x=Z) определяется x=A w (a)=b VA-p5P a»6″ /a 10.58[0.83] Р, _9, 75a3EJ3E. Ф2′ В x-w (for)=В o3a14RA3EJ2 (Over)от 3 до 6 в2 (2A)3 6£L 4A8RA3 15 80RA3-R= (» 1 0 −5 8 • 3 — 2,33 + 22,5 — 4 — 0,222)— = — • Определение линейных и угловых перемещений других участков балки также
не представляет трудностей. Прутки с непрерывно изменяющимися размерами поперечного сечения по длине. Если размеры поперечного сечения стержня изменяются непрерывно, то формула, полученная на основе гипотезы плоского поперечного сечения, вообще говоря, неверна(как и сама гипотеза). Однако для некоторых точных решений теории упругости можно использовать, конечно, обычное условие прочности и дифференциальное уравнение упругой линии, т. е. упругой линии, если угол наклона образующей поверхности стержня к его ОСП мал (не превышает 15-20°), то достаточен для инженерной практики. <<Г И d2w, _m (x)dx2EJ (x) • (10.141) Поскольку тангенциальное напряжение более чувствительно к наклону формируемой поверхности стержня, формула Журавского при применении ее к стержням переменного сечения дает значительные погрешности. 302 расчет прочности и жесткости стержней переменного сечения осложняется тем, что момент сопротивления и момент инерции поперечного сечения являются функцией абсциссы X-сечения. На это указывают обозначения формул (10.140) и (10.141). Последнее выражение может быть записано в несколько измененном вид
е. Вводится понятие изгибающих моментов, показывающих момент инерции (обычно максимальный или минимальный) любого сечения по Jo: MPR (x)=M (x)-j^-’(10.142) далее умножаем числитель и знаменатель (10.141) правой части выражения、 «Литий м» р (х)<1х*==(10.143) Это выражение по своему виду совпадает с выражением (10.135), но имеет другое значение, которое содержится в значении L1pr(x) выражения. Частным случаем балки с непрерывно изменяющейся площадью поперечного сечения является балка с равным сопротивлением изгибу, то есть во всех сечениях, где максимальное напряжение равно допустимому напряжению. Г /Я-Им Ж Я «Кукуруза Ж Таким образом, получено уравнение для определения размеров пучка равного сопротивления: Закон это меняет. Г(х)=^—(10.144) Учитывая произвольную форму сечения (и таким образом, что
его размеры определяются только одним параметром), из уравнения (10.144), по длине балки, следовательно, мы можем использовать уравнение упругой линии (10.143), чтобы найти все перемещения. Ищите форму консоли с равным сопротивлением изгибу. Сечение представляет собой прямоугольник с постоянной шириной b и переменной высотой(рис. 291). Затем укажите высоту балки в любом сечении Через H(х). Кроме того, это ясно, /М(х) / =РЗ. Таким образом, 303 следует уравнению(10.144), bh2 (х)РЗ 6~Т Г Г’ Откуда *«=/- Щ-к». Таким образом, высота рассматриваемых Пучков равного сопротивления изменяется по параболическому закону(рис. 291, 6). В то же время «•- Но- Поскольку изгибающий момент мал вблизи конца (I»=0), высота детали определяется условием прочности Tmax ’Tmax’ —2 ′ [T], Откуда 2H [t] построенная балка параболической формы является наиболее приемлемой с точки зрения экономии материала, но из-за сложности формы
не соответствует техническим требованиям. Поэтому это одна из целей ступенчатого стержня, равенство балки, которая не применяется на практике. Ситуация аналогична ситуации с двутавровыми балками, круговыми и другими типами секций. Существует очень простой контур, который широко используется в листовых пружинах, и своеобразная балка равного сопротивления-прямоугольная балка постоянной высоты h и переменной ширины b (K). Найдите форму балки с равным сопротивлением изгибу для схемы, показанной на рисунке. Поперечное сечение балки представляет собой прямоугольник с постоянной высотой h и переменной шириной b (x). Для того чтобы определить форму балки для симметрии, достаточно рассмотреть только левую половину пролета.
Тогда, если мы подставим M (x)=4-(IX)=•эти выражения в Формулу (10.144)、 Откуда Б-Л » [Св.] Ширина сечения изменяется по линейному закону, поэтому балка прикладывается к фиг. Есть формы, показанные в 292, B. максимальная ширина моста находится в середине пролета: 3PZ д а м Определим максимальное отклонение f этого луча. В соответствии с формулами (10.142) и (10.143)、 Dchu МНР(Ч) Т×5″ «, е / о Куда? Четыре. Я В этом примере Г. г м3.(Ф) * J о — — — — — — — -, J в(Х) — ———-. Так что это Да. ^ 0 _ Т (*Г~Б (х)2х * И, Я икс • La / \R I R1MPR’~’ Для риса. 292, b показаны графики M и Q, а также графики приведенных изгибающих моментов. Таким образом, дифференциальное уравнение упругой линии левой половины пролета принимает вид L R1 ЛС »» 4Е/0 Интегрируя его дважды、 [-Д-Х2+СХ+п]. ЭДЖ чтобы найти w w-n Z R9 константы C и D, мы используем симметрию упругой линии(это обозначено ломаной линией
на рисунке. 292, а): Sch (0) равно 6(4 1= Отсюда икс.] 305bit, Так что ж И, (4)1 / Pl I2PF I \ o\8 4 8 2 / f=w\2 литр 32., Если пучок имеет определенное поперечное сечение, то из условий интенсивности видно, что он прямоугольный в плане(пучок с определенной шириной) фиг. 292 ″ b обозначается пунктирным контуром). Для таких балок максимальное отклонение/’ — t y g — < / <и 4 5>следовательно, балка равного сопротивления имеет вес в два раза меньше, чем балка определенного поперечного сечения, и ее максимальное отклонение равно (10,146).) Ширина поперечного сечения опоры b должна определяться из условия прочности Tmax. Однако размер балки оказывается незначительным, и обычно прочность концов обеспечивается конструктивным устройством, необходимым для поддержки балки. Расчет обычных пластинчатых пружин(рис. 293,
г), состоящая из пакета листов, приводится к расчету балки, который считался справедливым. Мы рассуждаем следующим образом. Отрежьте луч равного сопротивления(рис. 293, а) на полосе, как показано на рисунке. Добавьте ту же полосу 293, b и ширину y. в результате мы получим широкую полосу n /=- И , п Как использовать 293, E. сложив эти полосы вместе, мы получим то, что представлено на рисунке. 293g листовая пружина. Если все листы соединены вместе(например, сварные или клепаные), то получается балка с определенной шириной t и переменной высотой поперечного сечения. В пружинах листы не соединены друг с другом(зажимы,
доступные в пружинах, полезны для обеспечения того, чтобы пружины не разваливались) и могут грубо предположить, что все полосы получают одинаковую кривизну при деформации. Тогда сумма полос в пружине, с точки зрения напряжения и деформации, эквивалентна сумме полос, показанных на рисунке. 293, Б, т. е. балка равного сопротивления постоянной высоты и переменной ширины(фиг. Итак, для 293, а) такой пружины условие прочности (N*= = tn) принимает вид (10.147) И максимальное отклонение[см. равенство (10.146) 1f=l, 5f’=1.5(10.148) Куда? г bji3_Ink3 «T U» ~ » 12″ * Как использовать 294, а, соответствующий пучок равного сопротивления имеет форму треугольника(рис. 294, Б) и, очевидно,, От.™ 3ja9 «/II6YA PMLX » — ~y G•так что условие прочности имеет вид.— = < [<71, (10.149) Отметим, что пружина изготовлена из высокопрочной стали, поэтому обычно величина[o] достигает более 4000 кгс/см2. Что касается прогиба пружины, то оказалось, что на практике (в основном за счет трения между листами) он меньше, чем у соответствующих балок равного сопротивления, поэтому используются формулы (10.148)
и (10.150).) Но Немногие люди- Пример 47, пружина (рис. 292, 293) состоит из семи полос с поперечным сечением длиной 100 см, 60×8 мм и нагружается силой Р= = 750 кгс. Необходимо проверить прочность пружины ([<g]=4500kgf / cm?) И найти максимальное отклонение. В этом случае l=0.8 cm;/=6cm; I=100cm; P=750kgs; l= = 7, то 6 * 7.0, 8? Двенадцать. см * =1,79 см*. STM a= — ^^ — d t/b75 к C согласно состоянию прочности(10.147)?-Я не уверен. о°^в КГС/см3=4180kgf/см3<4500kgf / см3. Таким образом, пружина сильная. 307 далее, если использовать формулу (10.148) и заменить коэффициент 1.6 на Р、 p / W750, I0Q3^=P48E70= 0 ^ 4 — 1, 4 0 ) 4 8.2,1 * 10E•1,79 s m=(1.2 5 4 −1,4 0 )4,1 6 cm==5.2-g-5.8 cm, то есть максимальное отклонение находится в пределах 52-58mm. В заключение следует отметить, что приведенный выше метод расчета пластинчатой пружины в определенной степени условен, так как не учитывает трение между пластинчатыми пружинами;1) фактически пластинчатые пружины не используются.
Смотрите также:

