Прямоугольная изометрия
В прямоугольной изометрии аксонометрические оси расположены под равными углами друг к другу (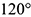
).
Для прямоугольных аксонометрий получена расчетная формула по коэффициентам искажения:
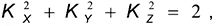
т. е. сумма квадратов коэффициентов искажения равна двум [12].
В прямоугольной изометрии коэффициенты искажения равны и по приведенной формуле получается, что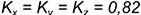 
. Для построения прямоугольной изометрии пользуются приведенными коэффициентами искажения, округленными до единицы, то есть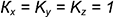 
Аксонометрическая плоскость прямоугольной изометрии равнонаклонена ко всем трем плоскостям проекций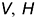 
и 
и 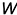пересекает эти плоскости проекций по равностороннему треугольнику, который называют треугольником следов. Следовательно, аксонометрические оси прямоугольной изометрии являются высотами, биссектрисами и медианами этого треугольника, а точка 
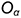их пересечения является точкой начала аксонометрических координат. Как известно из геометрии, углы между высотами равностороннего треугольника равны 120 градусам и соответственно углы между аксонометрическими осями также равны .
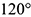На рис. 10.3 показано расположение аксонометрических осей в прямоугольной изометрии (ось «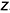
» всегда располагается вертикально), размеры и расположение больших и малых осей эллипсов и их построение одним из известных способов.
Большие оси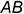 
всех трех эллипсов равны 
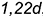, где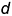 
— диаметр окружности, а малые оси 
эллипсов равны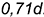 
.
Ориентация больших и малых осей эллипсов относительно аксонометрических осей:
-эллипс 1: аксонометрическая проекция окружности, лежащей на проекциях предмета в плоскости, параллельной плоскости проекций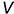 
: большая ось эллипса перпендикулярна аксонометрической оси 
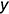, а малая ось совпадает с осью ;
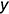-эллипс 2: аксонометрическая проекция окружности, лежащей на проекциях предмета в плоскости, параллельной плоскости проекций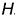 
: большая ось эллипса перпендикулярна аксонометрической оси 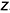, а малая ось совпадает с осью ;
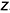-эллипс 3: аксонометрическая проекция окружности, лежащей на проекциях предмета в плоскости, параллельной плоскости проекций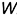 
: большая ось эллипса перпендикулярна аксонометрической оси 
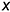, а малая ось совпадает с осью .
На рис. 10.3 показан один из способов построения четырехцентровых овалов, которыми на чертежах заменяют эллипсы в прямоугольной изометрии.
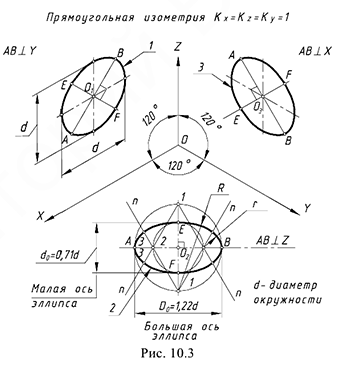
Графические действия для построения овалов следующие:
- провести две концентрические окружности, диаметры которых равны размерам большой и малой оси эллипса с центром в точке
; - из двух центров в точках 1, лежащих на окружности большой оси, провести две большие дуги радиусам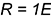и
и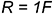 
; - из точек 1 провести прямые
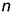через точки 2, лежащие на окружности малой оси; - на пересечении проведенных дуг и прямых 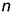получить точки 3, которые определяют окончание больших дуг;
- из двух центров в точках 2 провести две малые дуги радиусам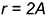и
и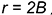 
до точек 3.
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:
| Развертка поверхности открытого тора |
| Аксонометрические проекции |
| Косоугольная (фронтальная) диметрия |
| Прямоугольная диметрия |
