Задача №160.
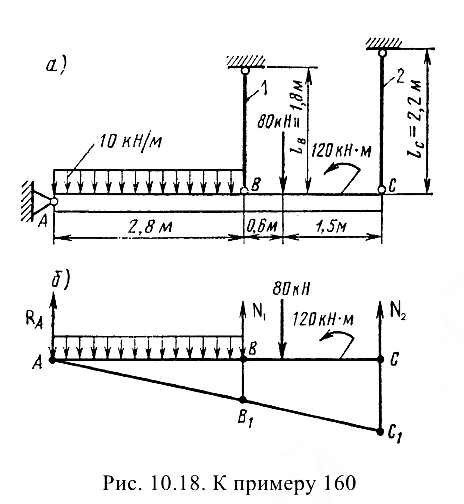
Проверить прочность тяг, поддерживающих весьма жесткую балку, изгибом которой можно пренебречь. Балка шарнирно укреплена в стене, как указано на рис. 10.18, а. Тяги одинакового поперечного сечения площадью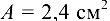 
выполнены из стали, допускаемое напряжение для которой задано: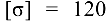 
.
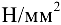Решение:
Превратим балку в свободное тело. Для этого отбросим опоры и заменим их действие реакциями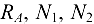 
. Силы, действующие на балку, представляют собой систему параллельных сил, для которой можно составить два независимых уравнения равновесия:
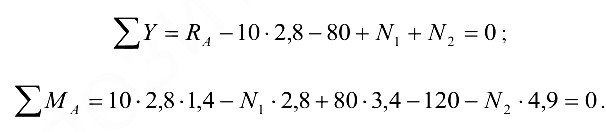
Уравнений равновесия два, а неизвестных — три, следовательно, система один раз статически неопределима. Составим уравнение перемещений. Балка повернется вокруг точки 
на некоторый угол, не деформируясь, и примет некоторое наклонное положение (рис. 10.18, б).
Вертикальные перемещения шарниров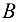 
и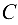 
соответственно равны удлинениям тяг, вызванных действием на них растягивающих сил, равных и противоположно направленных реакциям 
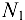и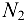 
. Выразим удлинения стержней:
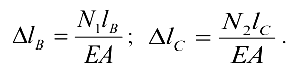
Из подобия треугольников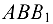 
и 
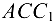получим
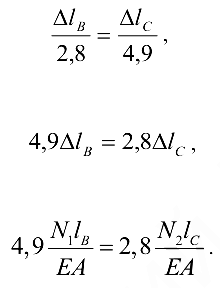
Жесткость сечений тяг одинакова, поэтому
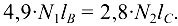
Подставим значения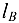 
и 
и 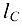получим зависимость между реакциям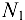и и :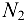
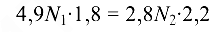
откуда
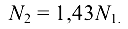
Подставив найденное выражение в уравнение моментов, получим 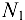= 19,5 кН, тогда 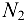= 28 кН. Более нагружена тяга 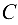. Найдем напряжения растяжения в ней:
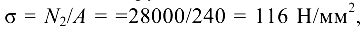
что меньше допускаемого напряжения; значит, прочность тяг обеспечена.
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:
