Пример задачи 8.1
Проверить прочность и жесткость стальной консольной балки составного поперечного сечения (рис. 8.5, а), если нагрузка F направлена под углом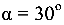 
к вертикальной оси сечения.
Для материала балки R = 210 МПа, Е = 200 ГПа.
Допустимый относительный прогиб балки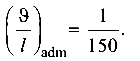 
Для определения прогиба на конце консоли (т. В) следует воспользоваться формулой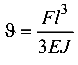 
, взятой из справочника.
Решение
Внешняя сила действует на балку перпендикулярно ее продольной оси и не совпадает ни с одной из главных центральных осей сечения ХУ.
Следовательно, рассматриваемая балка подвергается деформации косого изгиба.
Разложим силу F на составляющие по направлению главных центральных осей сечения (рис. 8.5, б):
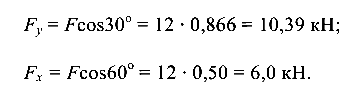
Вычислим значения изгибающих моментов для характерных сечений балки в главных плоскостях (в вертикальной и горизонтальной).
- В вертикальной плоскости:
- в сечении В
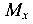= 0; - в сечении А
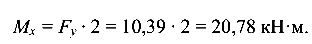
- В горизонтальной плоскости:
- в сечении В
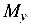= 0; - в сечении А
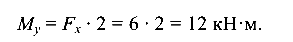
Эпюры изгибающих моментов строятся отдельно в вертикальной и горизонтальной плоскостях (рис. 8.5, в).
В примере опасным является сечение А, где оба изгибающих момента достигают максимальных значений.
Поскольку сечение балки имеет две оси симметрии и нескруг-ленные углы, для ведения расчета целесообразно использовать условие прочности в виде (8.2):
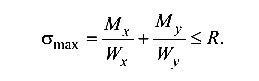
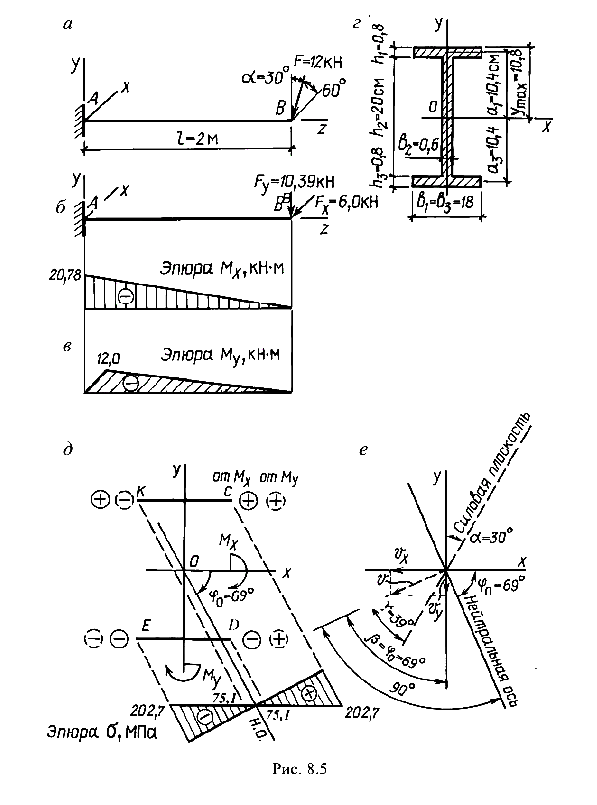
Приступим к вычислению геометрических характеристик сечения балки. Для вычисления моментов инерции сечение необходимо разделить на три прямоугольника (рис. 8.5, г). Вследствие симметрии сечения центр тяжести его очевиден.
Следует обратить внимание, что оси Y всех трех прямоугольников, составляющих сечение, совпадают, а оси X — нет. При вычислении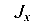 
необходимо учесть переход к параллельным осям.
Моменты инерции сечения относительно главных центральных осей:
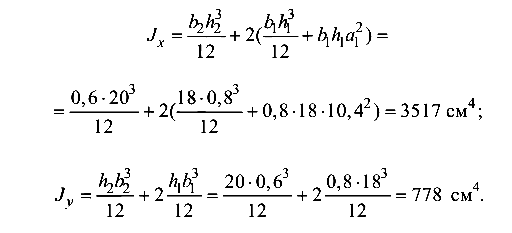
Моменты сопротивления сечения
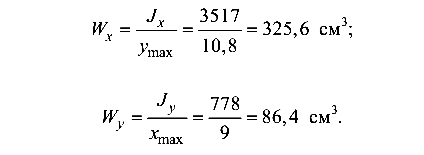
Перейдем к вычислению нормальных напряжений в балке. Значение максимального нормального напряжения в опасном сечении балки (сечение А)
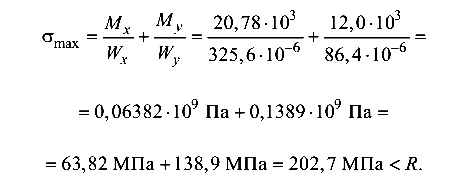
Из результата вычисления следует, что прочность балки обеспечена.
Для установления наиболее напряженной точки опасного сечения следует знать положение нейтральной оси в этом сечении, которое определяется из формулы (8.1):
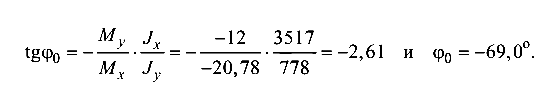
Заметим, что в формуле (8.1) следует учитывать знаки изгибающих моментов.
Отрицательное значение угла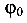 
откладываем от оси X по ходу часовой стрелки (рис. 8.5, д).
Знаки нормальных напряжений в точках сечения устанавливаются исходя из зоны растяжения и сжатия.
Так, часть сечения А, расположенная выше оси X, от изгибающего момента 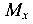растянута 
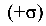, а часть, расположенная ниже оси X, -сжата 
.
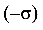От изгибающего момента 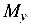растянута часть сечения, расположенная справа от оси Y, и сжата расположенная слева (см. рис. 8.5, д).
Определим нормальные напряжения в характерных (угловых) точках опасного сечения А, используя ранее вычисленные его составляющие:
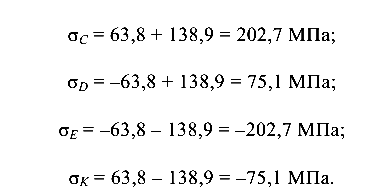
Суммарная эпюра нормальных напряжений показана на рис. 8.5, д. Заметим, что максимальные нормальные напряжения находятся, как и при плоском изгибе, в наиболее удаленных от нейтральной оси точках (точки С и Е).
Завершим пример рассмотрением перемещений балки. Вычислим значения вертикального и горизонтального прогиба свободного конца балки (сечение В):
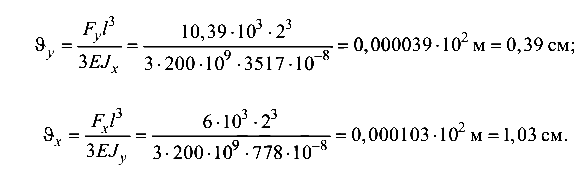
Суммарный абсолютный прогиб конца балки (рис. 8.5, е)
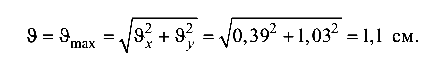
Относительный прогиб
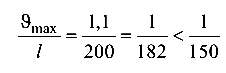——жесткость балки обеспечена.
Полный прогиб балки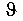 
направлен перпендикулярно нейтральной оси, под углом
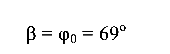
к вертикальной оси Y сечения и под углом
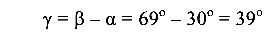
к силовой плоскости (рис. 8.5, е).
Поскольку в любом сечении рассматриваемой балки отношение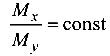
, изогнутая ось балки представляет собой плоскую кривую.
Этот пример решения задачи взят со страницы решения задач с примерами по всем темам предмета «Сопротивление материалов»:
Примеры решения задач по сопротивлению материалов
Дополнительные задачи которые вам будут полезны:
