Простейшие правила вычисления производных

Оглавление:

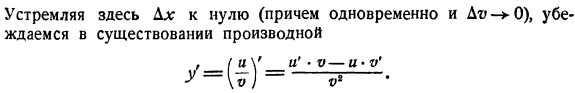
Простейшие правила вычисления производных

Простейшие правила вычисления производных. В предыдущем разделе мы рассчитали производную элементарной функции. Здесь и в следующем выпуске мы устанавливаем некоторые простые правила, по которым мы можем вычислить производную функции, состоящей из основных функций, конечным числом арифметических операций и суперпозицией[n°2b]. I. предположим, что функция u = y (x) имеет производную u ’ (в некоторой точке x;).Докажите и вычислите, что функция y = cu (c = cn $ 1) также имеет производную (в той же точке). Когда независимая переменная x получает инкрементный Ax, функция получает инкремент Ли, который идет от исходного значения к значению s -| Ды.

Это выражение представляет данное правило. Людмила Фирмаль

Новое значение функции y равно y \ Au = = c (k Di)*и поэтому новое значение функции Y равно Нш1г〜=с•Нш〜=с-и、 &x-0LX Таким образом, производная существует и равна г =(С-А)’ = С * Н’. Коэффициенты константы могут быть выведены по знаку производной. Второй. Функция «= <р(х), р =φ (() имеет производную (в некоторой точке), А’, Р».Докажите, что функции y =и±y также имеют производные (в той же точке)и вычислите их. дадим х приращение Ах. И V и y каждый получают приращение D’, Au, Du. Их новые значения u \ Au, yAy и yAy связаны с одним и тем же отношением. Отсюда г -) ды =(м-|-ды)±(в + Ай). АУ = Лю±ДГ, Т = 7 * А-А-А..

Делай, Делай, Делай. 、 1Н-Р〜= 1sh1 1-р БМ РТ = 1Р:±РЛ ДХ * 0 ^ * ДХ °Д * х * 0 ^ х Производная Y существует и равна / =(п± ’ г)’ = у±г Этот результат можно легко распространить на любое количество терминов (кроме того, таким же образом). III. при тех же предположениях о функциях u, V докажите, что функция y = u-y также имеет производную, и найдите ее. Приращение Dx соответствует приращению Li, Do и Du, как уже упоминалось above. At в то же время, если Du =(и -} Dm) (•») Up)、 Дю =V день и•на + день•в И затем Ди, ду, Ди а р-=—В—и• — к-к -«. Dx 1 Dx 1 Dx Dx Дх * 0 когда N ° 82, 2°, и Da * 0 спасибо、 Золото д * * * О ^ = И HJ ^ * о / т.

Чтобы доказать это, мы можем использовать метод математической индукции. Людмила Фирмаль

Светлейший ^ = 1 / .|у * О ’> б * й-0d С * Д * * О ^ х〜 То есть производная y существует и равна У =(У•О / = «’* о 4〜К * О’. если y = mn&, и’, o’, yes ’ существуют、 г = [(от). да] ’ =(а)’•Да («Г»)* Да ’= я’oda + ОТ’ЗР + дать \ для n факторов это будет то же самое. н [Дать… 5] ’ = I’oda … 5 + но’да… $ +Йод’ … $ … +Йод… 5 ′. IV. наконец, если и, о удовлетворяет предыдущему предположению, и о не равно нулю、 Функция= = ^также имеет производную и находит ее. В той же нотации, что и выше、 Г + к = И затем Как это А то. D c * o-и * Do V(o + Do） Ди. Ты можешь это сделать. Dh. В-а потом К Dh. О(О-| делать） И+ К О | К 9 Здесь стремится к нулю Ax (в то же время, Da ► ()), производная равна В * , (И\ r и ’•V-и-V.

Производная обратной функции.	Производная сложной функции.
Формула для приращения функции.	Односторонние производные.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.