Оглавление:
Производные высших порядков
Пусть функция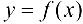 
определена на множестве X и имеет производную в точке 
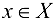и некоторой ее окрестности. Тогда производная функции 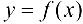в точке х есть функция 
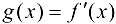. Если функция 
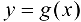имеет производную 
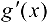в точке 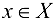, то функцию 
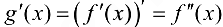называют производной второго порядка функции 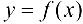и обозначают 
.
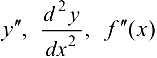Вторая производная функции 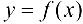может существовать в точке х и некоторой ее окрестности. Тогда, если существует производная второй производной, то ее называют производной третьего порядка и обозначают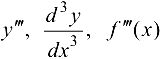 
Продолжив аналогичные рассуждения, получим, что если функция 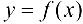имеет в точке х и некоторой ее окрестности все производные до n-го порядка включительно, то производная от
будет представлять собой производную n-го порядка. Если при этом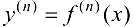 
— непрерывная функция на множестве X, то функция 
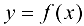называется п раз непрерывно дифференцируемой функцией или функцией класса 
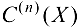. Функция, имеющая производную любого порядка, называется бесконечно дифференцируемой.
Пример 5.14.
Функция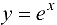 
— бесконечно дифференцируемая функция па множестве 
.
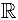Если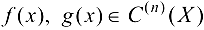 
, то
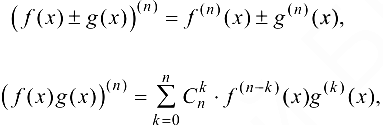
где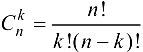 
. Формула (5.13) называется формулой Лейбница.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
