Если функция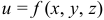 
дифференцируема в точке 
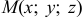, то она имеет производные по всем направлениям и справедливо равенство:
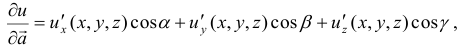
где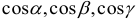 
— направляющие косинусы вектора 
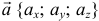, определяемые формулами 
.
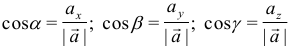Градиентом функции 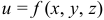называется вектор 
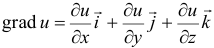. Градиент функции 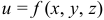в точке 
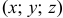направлен в сторону наибольшего роста функции 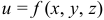, а длина его равна скорости роста функции в этом направлении и
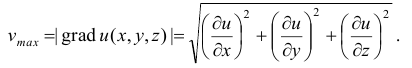
Пример:
Пусть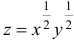 
. Найти a) 
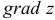в т. 
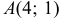; б) производную функции 
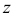по направлению вектора 
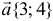в т. 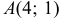; в) построить линию уровня, проходящую через точку 
.
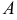Решение:
а)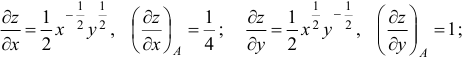 
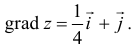
б) Вычислим производную функции в т. 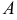по направлению вектора 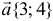. Для этого найдем направляющие косинусы вектора 
:
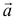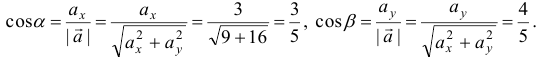
Подставляя в формулу производной функции по направлению вектора значение частных производных и направляющих косинусов, получим значение производной функции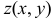 
по направлению вектора 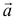в т. :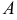
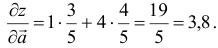
в) Найдем значение функции 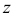в т. :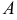 
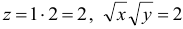— линия уровня функции, проходящей через т. 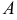. Возведем обе части в квадрат и выразим 
: 
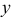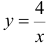— гипербола, расположенная в первой четверти (О.О.Ф. 
).
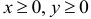Следует обратить внимание, что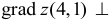 
(ортогонален) касательной к линии (гиперболе) в т. 
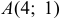. Этот частный факт есть иллюстрация общего случая: градиент в точке 
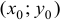всегда ортогонален линии уровня, проходящей через точку .
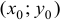На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Экстремум функции нескольких переменных |
| Условный экстремум |
| Наибольшее и наименьшее значение функции z=f(x,y) |
| Метод наименьших квадратов |
