Оглавление:
Производная по направлению и градиент
Пусть функция 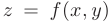 определена в области
определена в области 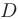 . содержащей точку
. содержащей точку 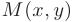 . Зададим некоторое направление
. Зададим некоторое направление 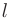 косинусами углов
косинусами углов 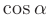 и
и 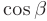 , образованных лучом
, образованных лучом 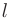 с осями
с осями 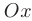 и
и 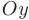 . При перемещении в направлении
. При перемещении в направлении 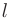 точки
точки 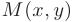 в точку
в точку
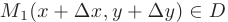
функция получит приращение
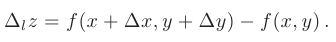
Обозначим через 
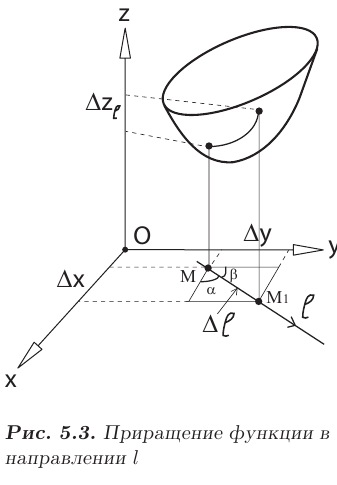
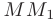 — величину перемещения точки
— величину перемещения точки 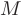 (см. рис. 5.3). Тогда, под производной
(см. рис. 5.3). Тогда, под производной 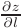 функции
функции 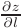 в заданном направлении
в заданном направлении 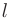 понимается предел отношения приращения функции в этом направлении к величине перемещения, когда последнее стремится к нулю:
понимается предел отношения приращения функции в этом направлении к величине перемещения, когда последнее стремится к нулю:
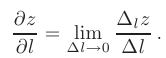
Величина производной 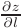 ответствует скорости изменения функции
ответствует скорости изменения функции 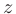 в направлении
в направлении 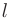 . Формула для вычисления производной функции
. Формула для вычисления производной функции 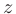 в заданном направлении
в заданном направлении 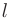 имеет вид
имеет вид
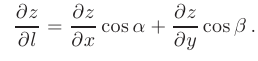
Очевидно, что частные производные 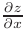 и
и 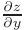 представляют производные по направлениям, параллельным осям
представляют производные по направлениям, параллельным осям 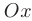 и
и 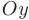 соответственно.
соответственно.
Градиентом функции 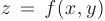 называется вектор с координатами
называется вектор с координатами 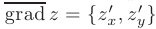 . Рассмотрим скалярное произведение векторов
. Рассмотрим скалярное произведение векторов 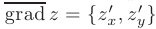 и единичного вектора
и единичного вектора 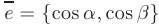 :
:
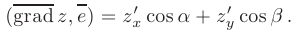
Сравнивая последнюю формулу с формулой производной по направлению, делаем вывод, что производная по направлению есть скалярное произведение вектора градиента 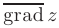 и единичного вектора, задающего направление
и единичного вектора, задающего направление 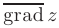 :
:
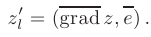
Известно, что скалярное произведение двух векторов максимально, если они сонаправлены. Следовательно, градиент функции в данной точке соответствует направлению максимальной скорости изменения функции в этой точке. Можно доказать, что градиент функции в данной точке перпендикулярен линии уровня, проходящей через эту точку.
Пример:
Задана функция 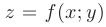 и координаты двух точек на плоскости:
и координаты двух точек на плоскости:
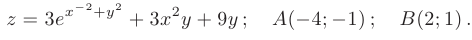
Требуется определить направление максимальной скорости изменения функции в точке 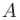 и скорость изменения функции в направлении вектора
и скорость изменения функции в направлении вектора 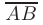 в этой точке. Построить единичные векторы градиента функции и направления
в этой точке. Построить единичные векторы градиента функции и направления 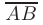 в точке
в точке 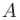 в системе координат
в системе координат  .
.
► 1. Используя таблицу основных производных и правила дифференцирования сложной функции, найдем частные производные первого порядка 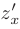 и
и 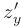 для указанной функции:
для указанной функции:
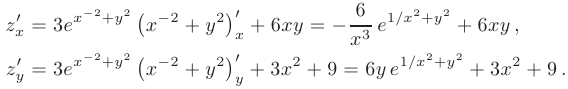
Вычислим значения частных производных в точке 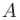 (—4; —1):
(—4; —1):
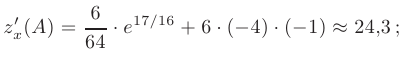
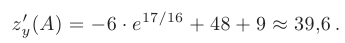
Направление максимальной скорости изменения функции двух переменных 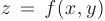 задается вектором градиента
задается вектором градиента 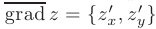 . Так как значения частных производных в точке
. Так как значения частных производных в точке 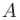 уже вычислены в предыдущем пункте, то можем записать искомый вектор:
уже вычислены в предыдущем пункте, то можем записать искомый вектор:
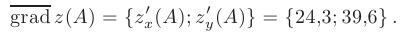
Для вычисления единичного вектора 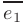 , сонаправленного с вектором
, сонаправленного с вектором 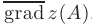 разделим координаты вектора градиента на его модуль в этой точке:
разделим координаты вектора градиента на его модуль в этой точке:
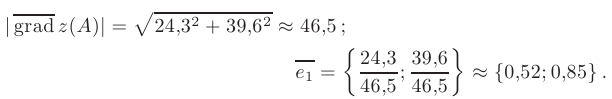
- Скорость изменения функции
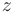 в направлении вектора
в направлении вектора  определяется ее производной в указанном направлении
определяется ее производной в указанном направлении 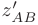 :
:
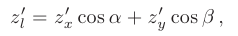
где 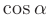 и
и 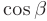 — направляющие косинусы вектора
— направляющие косинусы вектора  равные:
равные:
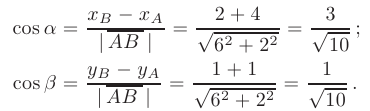
Таким образом
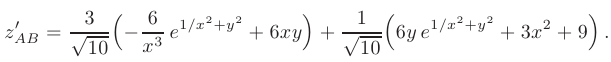
Единичный вектор 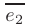 в направлении
в направлении  имеет приближенное значение:
имеет приближенное значение:
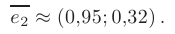
В результате, скорость изменения функции 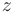 в направлении
в направлении  в точке
в точке 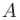 составит:
составит:
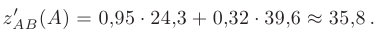
Вывод: Направление вектора  и направление максимальной скорости изменения функции
и направление максимальной скорости изменения функции 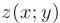 в точке
в точке 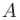 не совпадают:
не совпадают:
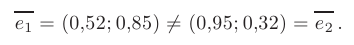
Следовательно, скорость изменения функции 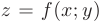 в точке
в точке 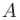 в направлении вектора
в направлении вектора 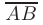 не является максимальной.
не является максимальной.
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:

