Производная обратной функции

Производная обратной функции

Пусть 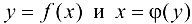— взаимно обратные функции.

Теорема 5.4. Если функция 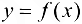строго монотонна на интервале 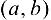и имеет отличную от нуля производную 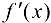в произвольной точке этого интервала, то обратная ей функция 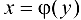также имеет производную 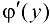в соответствующей точке, определяемую равенством .

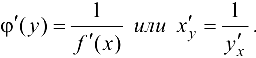Доказательство.

Рассмотрим обратную функцию 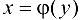. Придадим аргументу у приращение 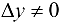. Ему соответствует приращение 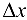обратной функции, причем 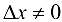в силу строгой монотонности функции 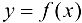. Поэтому можно записать

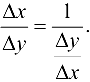
Если 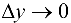, то в силу непрерывности обратной функции приращение 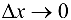. Так как 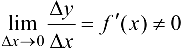, то из (5.9) следуют равенства . ■

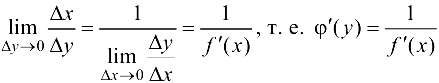Правило дифференцирования обратной функции записывают следующим образом:

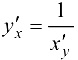
Пример 5.8.

Пользуясь правилом дифференцирования обратной функции, найти производную 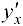. для функции .

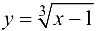Решение:

Обратная функция 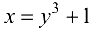имеет производную .

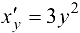Следовательно, .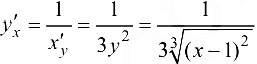

Ответ: .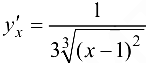

Пример 5.9.

Пользуясь правилом дифференцирования обратной функции, найти производную 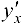, для функции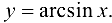

Решение:

Обратная функция 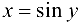имеет производную .

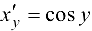Следовательно, .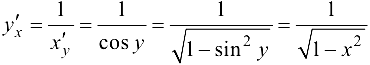

Ответ: .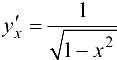

Эта лекция взята со страницы лекций по предмету математический анализ:

Предмет математический анализ

Возможно вам будут полезны эти страницы:

Вычисление производной алгебраической суммы, произведения и частного функций с примерами решения

Производная сложной функции с примерами решения

Производная функции, заданной неявно с примерами решения

Производная функции, заданной параметрически с примером решения