Оглавление:
Для понимания понятия производной решим две различные задачи, физическую и геометрическую, процесс решения которых приводит к возникновению одной и той же математической модели.
Задача 1.
Пусть тело движется прямолинейно и указан закон движения формулой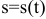 
, где 
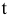— время движения, 
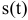— положение тела на прямой (координата движущейся материальной точки) в момент времени 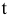. Найти скорость движения тела в момент времени 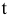, т.е. 
.
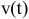Решение:
Предположим, что в момент времени 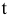тело находилось в точке 
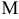, пройдя путь от начала движения 
.
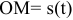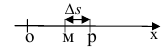
Дадим аргументу 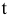приращение 
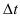, тело в момент времени 
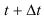будет находиться в точке 
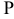, пройдя расстояние от начала движения 
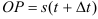. Значит, за 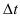тело прошло расстояние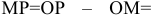 
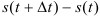. Полученную разность назовем приращением функции : 
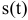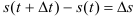. Итак, расстояние 
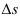тело пошло за время 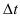. Найдем среднюю скорость 
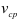, движения тела за промежуток времени 
:
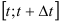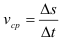
Естественно, что мгновенная скорость 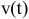— это средняя скорость движения за промежуток времени 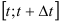при условии, что 
.
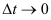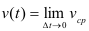или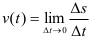 
Задача 2. Дан график функции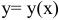 
. На нем выбрана точка 
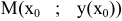, в этой точке к графику функции проведена касательная ( мы предполагаем, что она существует). Найти угловой коэффициент касательной 
.
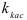При решении мы получим, что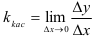 
.
Подведем итоги. Две различные задачи в процессе решения приводят к одной и той же математической модели — пределу отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю.
Определение. Производной функции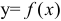 
в точке 
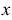называется предел (если он существует) отношения приращения функции к приращению аргумента при стремлении последнего к нулю: 
.
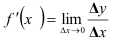Механический и геометрический смысл производной. Уравнение касательной к кривой в точке
A) 
Определение. Касательной к кривой 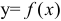в ее точке 
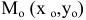называется предельное положение секущей 
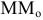, когда точка 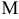стремится к 
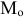вдоль данной кривой.
Угловой коэффициент касательной, проведенной к кривой 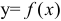в точке 
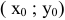, равен значению производной функции в абсциссе точки касания.
, 
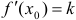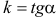, где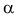 
— угол наклона касательной к оси 
.
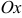Уравнение касательной к кривой 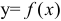в точке 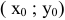имеет вид:
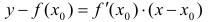
Пользуясь определением производной, мы можем вычислить производные для всех элементарных функций и составить таблицу производных.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Вычисление пределов с учетом их особенностей |
| Непрерывность функции в точке |
| Таблица производных, правила дифференцирования, производная обратной функции |
| Производная функции, заданной параметрически |
