Оглавление:

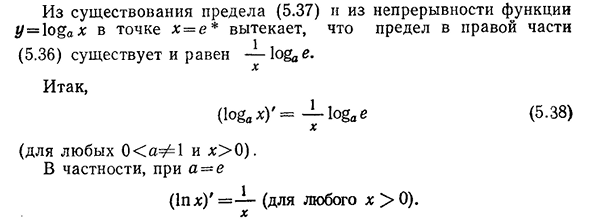

Производная логарифмической функции
- В точке x=^LP, где n= 0, ±1, ±2, ±3, …да что с тобой такое? Производная
логарифмической функции. Где 00-неподвижные точки. Далее, DX=+0, достаточно мало Ду ДХ Один. DH.
Один. Икс 1oea(х+ДХ) — 1oea х Dн По Людмила Фирмаль
определению, производная (105A x)’=NT — ^ — = — PT1o§a DX — * 0DX X DX — » 0 Икс (5.36)) Благодаря второму заметному пределу и элементарной
подстановке переменной I= х я 1SH1 171+ — G]=P t[(1+0′]=e.'(5.37)) ДХ-
- >0I\х/)/_>о Поскольку X > 0 фиксировано, (DX0DX — >0. X208 Глава 5. Дифференциальное исчисление Из непрерывности существования
предела (5.37) и функции y=1o^A X точка x=*e следует,что предел правой части (5.36) существует и равен -10^, 6. * Глава 2,§4,
Раздел 3 доказывает, что функция g/=1o§A x непрерывна в любой точке x>0. Людмила Фирмаль
Так… , (1о&, х)’= — y1o§е(5.38) (Для любых 00). В частности, a=e (1ph)’=—(для любого x>0).
Смотрите также:
| Производная по направлению. Градиент | Дифференциалы высших порядков |
| Частные производные высших порядков | Формула Тейлора с остаточным членом в форме Лагранжа и в интегральной форме |

