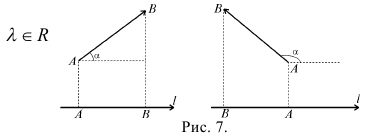
1. Векторной проекцией вектора 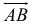 на ось
на ось 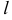 называется вектор
называется вектор 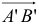 (рис. 7).
(рис. 7).
Проекция считается положительной, если вектор 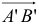 направлен также, как и ось
направлен также, как и ось  , и отрицательной, если направление оси и
, и отрицательной, если направление оси и 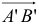 противоположны.
противоположны.
2. Скалярной проекцией вектора  на ось
на ось 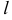 (
(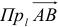 ) называется скаляр, абсолютная величина которого равна модулю векторной проекции того же вектора на ту же ось.
) называется скаляр, абсолютная величина которого равна модулю векторной проекции того же вектора на ту же ось.
3. Основные свойства скалярных проекций:
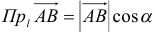 , где
, где 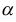 — угол между вектором
— угол между вектором 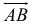 и осью
и осью 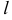 .
.-
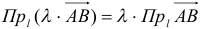 , где
, где  .
. 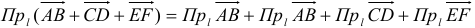
4. Если ось 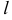 заменить некоторым вектором
заменить некоторым вектором 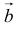 , то можно говорить о проекции вектора на вектор
, то можно говорить о проекции вектора на вектор 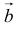 :
: 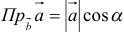 , где
, где 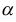 — угол между
— угол между 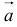 и
и 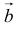 .
.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Системы линейных уравнений |
| Векторная алгебра: основные понятия и определения |
| Действия над векторами, заданными координатами |
| Скалярное произведение двух векторов |
