Пример №13.
Привести к каноническому виду следующую ЗЛП:
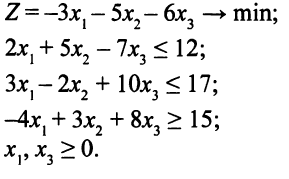
Решение.
- Так как переменная
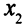может принимать любые значения, как положительные, так и отрицательные, представим ее как разность двух неотрицательных переменных, которые обозначим 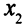и 
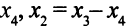. Переменную 
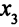теперь будем обозначать через 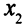. - Превратим два ограничения вида
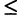в равенства, прибавив к их левым частям дополнительные неотрицательные переменные 
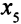и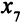 
. - Превратим ограничение вида
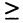в равенство, вычитая из его левой части дополнительную неотрицательную переменную 
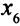. Дополнительные переменные 
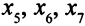не входят в целевую функцию 
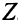. - В результате указанных преобразований целевая функция станет такой:
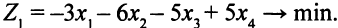. - Система ограничений примет вид:
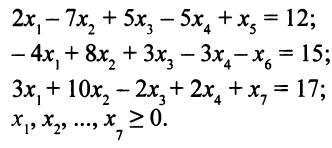
- Последнее, что осталось сделать — заменить целевую функцию
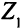функцией 
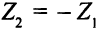и потребовать максимизации функции 
.
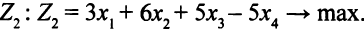Каноническая модель ЗЛП построена.
Если теперь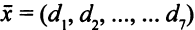 
— оптимальное решение построенной ЗЛП, то оптимальное решение исходной ЗЛП следующее:
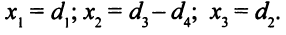
Эта задача взята со страницы решения задач по предмету «линейное программирование»:
Решение задач по линейному программированию
Возможно эти страницы вам будут полезны:
| Пример №10. Решить графически следующую ЗЛП |
| Пример №12. Фирма производит два вида продукции |
| Пример №14. Рассмотрим такую систему уравнений |
| Пример №15. Общий способ избавления от вырожденности |
