Присоединенный вихрь и подъемная сила

Присоединенный вихрь и подъемная сила

Присоединенный вихрь и подъемная сила. Давайте выясним, какое поле скорости определяется функцией 1 (% ) комплексной переменной^ = x + y! 。 Где-действительное число константы, а ее необычная форма описана ниже. Чтобы представить эту функцию в виде комплексного числа (то есть отделить действительную часть функции от мнимой), мы используем треугольное выражение, представляющее собой комплексное число% = ge»?、 r = d / x2 + y2-комплексный модуль 5, Φ= ags!»Аргументы При этом. Потенциал скорости потока Φ= Если вы приравняете функцию потока φ (x, y) к различным константам, вы найдете множество линий потока, показанных на рисунке. 16.10 описывает осесимметричное распространение жидкости от источника в начале координат.

Если в непрерывном потоке вокруг цилиндра такой поток перекрывает поток, то линия потока не фиксируется и совпадает с поверхностью цилиндра. Людмила Фирмаль

• Предполагая Φ= -, будет найдена другая диаграмма течения И φ= y-1n y / x2-1-y2 (это допустимо. Это объясняется тем, что действительная и мнимая части комплексной функции(16.12) являются гармоническими функциями. С этим Текущие дела Концентрические окружности (рис. 16.11) и линии эквипотенциала ГV По прямой, проходящей через Φ (χ, y)= ccs1 & concs1 Начало координат. Поток с таким полем скоростей называется свободным потенциальным вихрем. Важнейшей характеристикой поля скоростей потенциального вихря является циркуляция скорости по замкнутому контуру, охватывающему начало координат, которая описывается следующей формулой: Где u (x, y) вектор скорости в точке на контуре. I-единичный вектор, который касается контура в этой точке. $ 6-это базовая длина контура. И это проекция скорости на касательную контура. Рассчитаем скорость циркуляции по обтекаемой линии, представляющей собой окружность радиуса K.

By осевая симметрия потока, коэффициент скорости во всех точках этого круга, например, Формула (x, y)=■ / =И во всех точках окружности, поскольку скорость является касательной к текущей линии Как доказано теорией функций комплексных переменных, скорость циркуляции рассматриваемой задачи такая же, как и в случае замкнутых контуров, покрывающих начало координат. Таким образом, поле скорости задается постоянной гамма-функцией(I-19) (16.19). Когда вышеуказанный поток накладывается на поток при непрерывном обтекании цилиндра, концентрическая окружность 1, являющаяся линией потока, совпадает с окружностью, образующей границу цилиндра. 16 4 Обтекаемая диаграмма общего поля скоростей показана на рисунке 16.12.Рассмотрим поле давления на поверхности цилиндра этого field.

• Скорость жидкости 1иилинд, циркулирующей вокруг цилиндра, совпадает со скоростью, когда потенциальный вихрь 2 обтекает цилиндр и эти скорости. Нижнего полукруга, поэтому коэффициент скорости больше + U2 в каждой точке верхнего полукруга, коэффициент скорости в= U1 + U2 в соответствующей точке нижнего полукруга Каждая точка верхнего полукруга меньше давления рН соответствующей точки Нижнего полукруга, так что получается ненулевой подъем. Используя формулу (14 45) для определения давления на поверхности цилиндра, вычислите Интеграл (16 24) и исключите метрическую силу Архимеда、 Таким образом, в поле скорости, которое формируется, когда потенциальный вихрь прикладывается к потоку без циркуляции вокруг цилиндра, если потенциальная вихревая скорость жидкости по часовой стрелке, подъем p будет вверх.

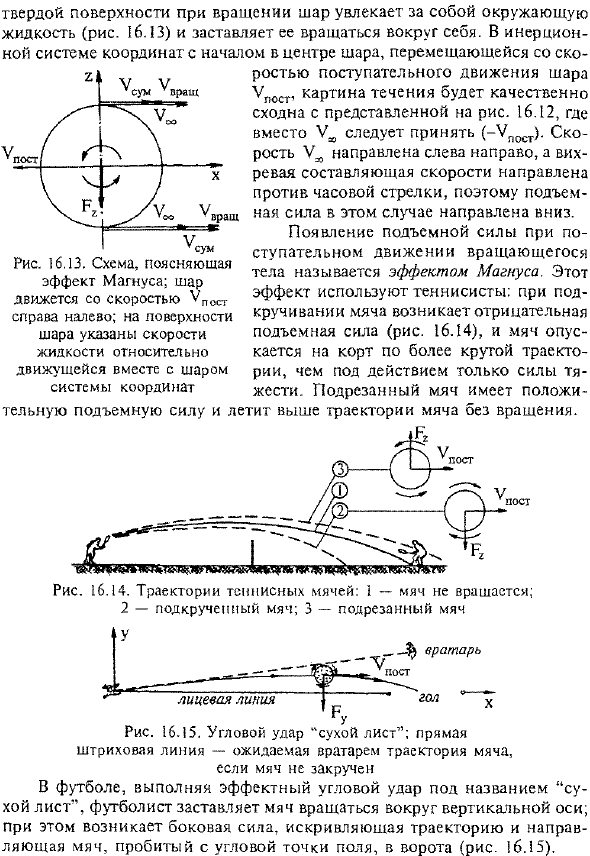
Выше показано, какими характеристиками должно обладать поле скорости при обтекании объекта, как действует подъемная сила, но пока не определено, как создается такое поле и какие условия формируются. Людмила Фирмаль

• Одним из простейших примеров формирования такого скоростного поля является воздушный полет со скоростью упосшера, который вращается вокруг горизонтальной оси за счет»прикрепления» жидкости. Поскольку во время вращения это твердая поверхность, шар переносит окружающую жидкость(рис. 16.13) и вращает шар вокруг себя it. In в инерциальной системе координат с началом координат центра шара, движущегося со скоростью поступательного движения Упостного шара, картина течения качественно аналогична той, что показана на Рис. 4. 16.12, принято вместо Y ^ (Post).Скорость V ^направлена слева направо, и состояние вихря равно.

Смотрите также:

Примеры решения задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Обтекание плоской пластины.
2. Безотрывное обтекание цилиндра однородным потоком невязкой жидкости.
3. Пограничный слой.
4. Отрыв пограничного слоя. Кризис обтекания.