Оглавление:


Принцип Сен-Венана
- Принцип Сания. Исследование изгиба не заботится о величине изгибающего момента, поперечных и вертикальных силах поперечного сечения, а также о том, как внешние силы прилагаются в то же время, когда нет силы в плоскости, проходящей через ось
центра изгиба. Выражая силу в виде вектора, момент делится на две стрелки, начало которых соединено прямой линией, а конкретная идея о том, как выполнять нагрузку,-это принцип Сен-Винаи. В главе I указывалось, что в сопротивлении материала невозможно заменить систему внешних сил, эквивалентных ему статически.
Принцип Сен-Венана смягчает это требование. Людмила Фирмаль
Согласно этому принципу, статически эквивалентную систему нагрузок можно заменить стержнем, который прикладывается к участку с размерами поперечных размеров стержня. Если на расстоянии от этой области и имеет одинаковый порядок величины, то изгибающие напряжения распределяются по закону плоского сечения, а величина главного вектора и главного момента приложенной силы зависит от принципа солнца-Венанта,
в частности, от сбалансированной системы сил, действующих на концы стержней, так что величина изгибающих напряжений зависит от угла наклона стержня. Для тонкостенных стержней, ситуация несколько иная. Ниже приведен простой пример, относящийся к 3. Власов убеждает нас, что сбалансированная система сил, приложенных к торцам тонкостенных стержней, создает напряжения на достаточно большом расстоянии от кромок.
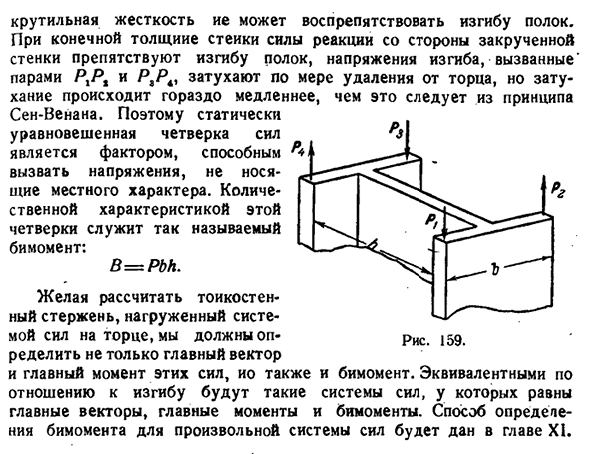
- Представьте двутавровую балку, нагруженную четырьмя одинаковыми продольными силами P1 ″ P1=W P1 = P4 = P, как показано на рисунке. 159 если стенка очень тонкая, пара Pt P загибает одну полку в своей плоскости, пара RGR^ — другую полку. Давление изгиба стойки достаточно далеко от края секции такое же. Стейки скручиваются, так как изгибы полок происходят в разные стороны. Но если стенка очень тонкая, то ее§ 110] VIECENTRAL stretch — — — —
сжатие 237 Крутильная жесткость s может предотвратить изгиб полок. Сила реакции на стороне стенки, скрученной конечной толщиной стержня, предотвращает изгиб полок, а напряжение изгиба, вызванное парой и P J\они отходят от конца.
Количественной характеристикой этой четверки является так называемый бимомент: Людмила Фирмаль
B=P B h. RG Наконец, для того чтобы рассчитать тонкостенный стержень, оснащенный системой сил, необходимо рассчитать не только главный вектор и главный момент этих сил, но и бимодальный изгибающий эквивалент-это система таких сил с равным главным вектором, главным моментом и биналь-ностью. Метод определения интерактивности для системы произвольных сил приведен в главе XI.
Смотрите также:
| Упруго-пластический изгиб | Внецентренное растяжение — сжатие |
| Несущая способность стержня при изгибе | Ядро сечения |

