Оглавление:

Примеры вычисления площадей.
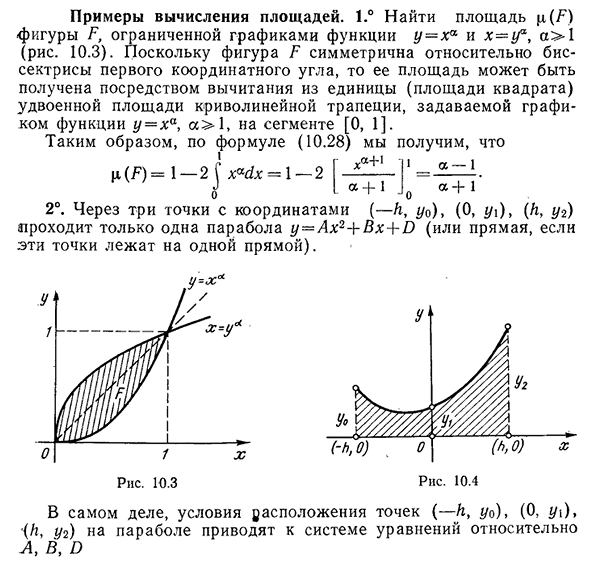
- Пример расчета площади. 1.Найдите область p (F) на рисунке F, окруженную графом функций °y=XA и x=ua, a>1(Рис. 10.3). Поскольку F
симметрична относительно биссектрисы первого координатного угла, то ее площадь равна площади трапециевидной кривой, заданной графом функции y=XA, CC>1 на отрезке[0,1].
Итак, по формуле (10.28), p Людмила Фирмаль
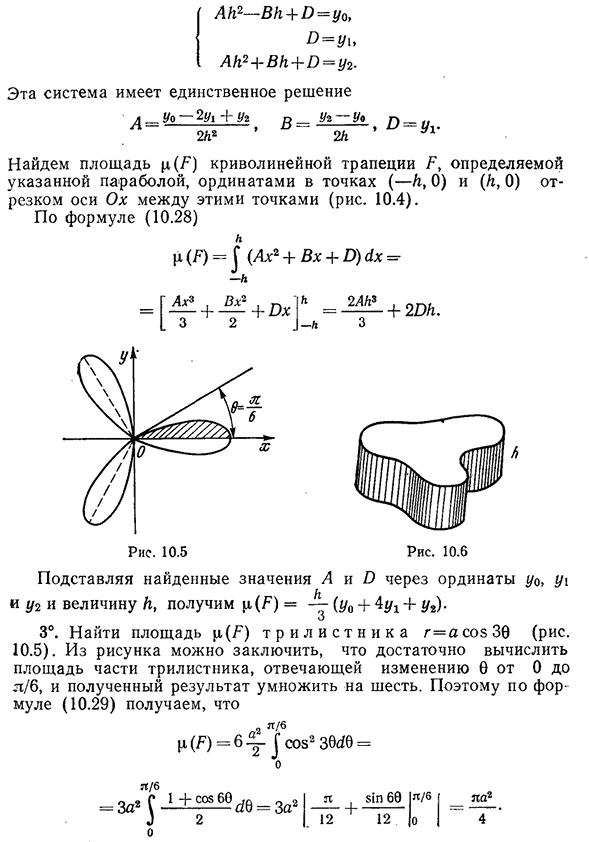
(F)=l-2f x^x=l-2 J L «+1Jo » +1 2°. Через три точки с координатами (- h, y0), (0, yi), (h, Y2) парабола y=Ax2+Bx+D (или прямая, если эти точки
находятся на одной прямой). Фактически, условия положения точек на параболе (—h, y0), (0, yi),\h, Y2) приводят к системе уравнений относительно a, B, d§3. Пространство 417, объем кузова Ah2-
- ЧД+Д=У0,г=г\, Ah2+БГ+Д=Г%. Эта система имеет одно решение. d_Uo-2U1Ug b=2h? Uz~Uo2h 9D=yx. Найти область p (F) криволинейной трапеции F, определяемую указанной параболой, и определить точки (—h, 0) и (/g, 0) по оси o отрезков между этими точками 10.4). По
формуле (10.28)) h p (F)=J{AH2+Bx-\ — D) dx= — h 2Ah3 2Dh. Рис 10,6 Три. Подставляя найденные значения A и d на вертикальные оси Uo, y\и g / 2 и значение h, получаем p(F)=-y (y0+4G/x4-Y2). 3°.
Найти область p (F) t p и l и C t n и K a r=A cos39(рис. 10.5). Из этого рисунка достаточно Людмила Фирмаль
вычислить площадь трилистника, которая соответствует переходу от 0 до 0 к L / 6, и результат можно умножить на шесть. Таким образом, по формуле (10.29) получаем 2l / 6 p (F)=6^ — J cos2 39tW= Отчет L / 6 =3<.>Дж Отчет 1 + cos60 2 dQ = Per2 Двенадцать. Грех 60 Отчет
Смотрите также:
| Повторные пределы | Случай функции двух переменных |
| Площадь криволинейной трапеции и криволинейного сектора | Понятие экстремума функции m переменных. Необходимые условия экстремума |

