Примеры определения деформаций графо-аналитическим методом

Примеры определения деформаций графо-аналитическим методом

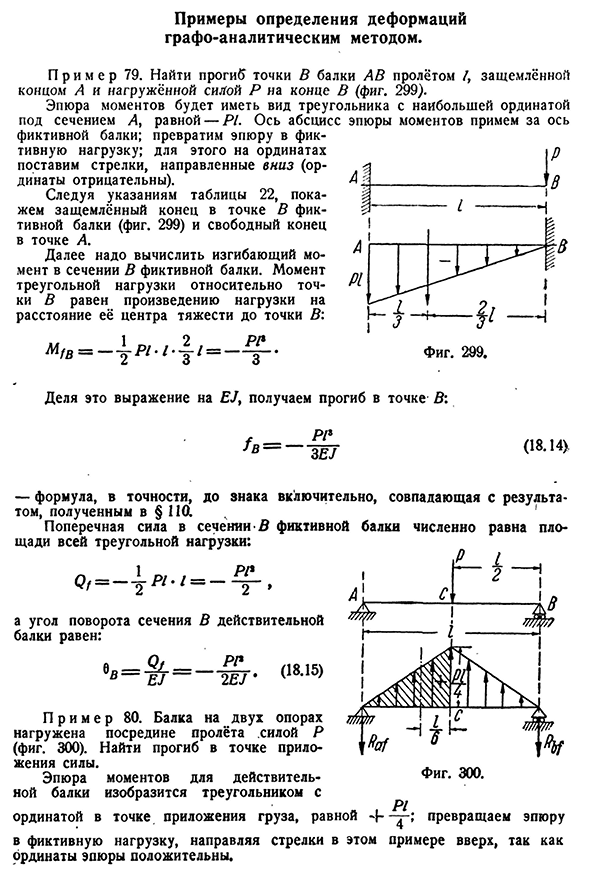
• Пример определения деформации методом графического анализа П р и М EP79. Найти точку отклонения балки AB span/, силу P, нагруженную на конце защемленного конца A и b(рис. 299). График момента имеет форму треугольника с наибольшей ординатой по сечению a, равной-P/. Для этого поместите стрелку вниз

(вертикальная ось отрицательна). Следуйте инструкциям в таблице 22, чтобы указать конец зажима точки B фиктивной балки(рис. 299) и свободные концы. Далее необходимо рассчитать изгибающий момент сечения фиктивной балки. Момент треугольной нагрузки относительно точки B равен произведению

нагрузки, обусловленной расстоянием от центра тяжести до точки B: Давайте Людмила Фирмаль

возьмем сюжет момента в качестве оси Разделите это выражение на EJ, чтобы получить отклонение B: Р-Р 3. (18.14) — Формула, точно, до знака включительно, согласуется с тем, что было получено в§нет. Сила сдвига поперечного сечения балки имитационной площади всей треугольной нагрузки:1 об / мин Результаты и-равно ООП- И угол

поворота фактического раздела луча: •» = > = —£■• <1815> Численно Фигура. 300. П р и М Е Р80. Балка на двух опорах нагружается в середину пролета силой Р(рис. 300). Вы найдете отклонение в точке приложения силы. График момента действительной балки представлен треугольником с вертикальной осью в момент приложения нагрузки равной+% P1 Поскольку вертикальная ось графика положительна, превратите сюжет в фиктивную нагрузку

• и направьте стрелки этого примера вверх.380ГР Афо-лирический и графический метод[гл. XIX в. Опорное устройство фиктивной балки определяется в соответствии с таблицей. 22 условия фиксации фактической симметрии будут равны между собой: Балки манекен балка опорная реакция сама по себе 1Pl P/2 2 2 ’4 16′ each равна половине целого Изгибающий момент сечения с равен моменту реакции (знак минус) плюс половина момента треугольной нагрузки^ p1I1 1П л Р Аф2^22 4 И так оно и есть. Ф-р-р-Дж-с-48EJ’ Угол поворота левой опорной секции равен y Q f A_A EJ~EJ~ ~ \6EJ’ Так как боковая сила опорного сечения равна опорной реакции (в данном случае, поскольку РДУ направлен вниз, она имеет знак минус).

Поддержка для: a-g R R Бабушка.- Один. ——- — Как видно из возможных примеров, при выбранных условиях для знака мнимой нагрузки, изгибающего момента и поперечной силы существует отрицательная запись формулы для прогиба.: П р и М Е Р81. Как показано на рисунке, угол поворота в конце балки A B графически анализируется. 301. На рисунке показана фиктивная балка с зоной нагрузки крутящего момента. Угол поворота для левой опоры равен: 1м, _Af_3 ’2М l_Mlа~Эдж-Эдж~6EJ’ Для правильной поддержки.: o_fy_3 ’2M l_M l in~E J~EJ-3EJ’§ 1 1 8] определение деформации методом графического анализа 3 8 1 П р и М Е Р82. В середине пролета найдите графически аналитически отклоненную до конца консоль для

балки (рис. 302). График изгибающего момента имеет форму трапеции с вертикальной осью наибольшего M= — P~a. N~поворот графика Людмила Фирмаль

в Фигура. 303. 1 11г ч Т1 г 1 2 В т в v1 ′ 1! 1? Фигура. Триста два Зона нагрузки путем направлять нагрузку вниз. Фиктивная балка зажата между концами и состоит из двух балок, поддерживающих балку подвески AB. Прогиб середины пролета (точка F) равен фиктивному моменту этой точки от равномерно распределенной нагрузки, деленной на жесткость: — H/1* _ P a / 2 —% EJ~8EJ * В момент прогиба определяется расчет манекена в момент этого прогиба. Нагрузка на мяч (рис. 302): RA2 / RA3 2 Это вызвано треугольником ke SA и реакцией прогона=RA•a2 3 И= Три. * Два. РА2[3/+2А]. Отсюда прогиб сечения C-MfC= — Afa. М/с_ _ ЭЖ » 6EJ П р и М Е Р83. Может быть. 303, найти отклонение секции графически. Построить график

изгибающего момента. В поперечном сечении, имеющем момент, равный m; в точке b он равен нулю. Изменения в соответствии с законом линией, проходящей через мгновение луч. Превратите участок М в фиктивную нагрузку и поместите воображаемую балку в соответствии с таблицей 22. Учитывая консоль AB, найдите вымышленный момент в точке B: AL1LV, 2, Mr Соответствующее отклонение будет:/a=√3√ *

Смотрите также:

• Примеры решения задач по сопромату

Дифференциальные зависимости при изгибе	Графо-аналитический метод при криволинейных эпюрах изгибающего момента.
Графо-аналитический метод.	Графический метод построения изогнутой оси балки.