Оглавление:





Примеры
- Образцы. П р и М Е Р11. Концы А и в прослоенных брусков выполнены из равных половин длины—(рис. 52, а); верхняя половина сделана из стали, нижняя из меди. Площадь обеих частей стержня одинакова и равна F=20CI2. Сила P=6t приложена к средней части, которая направлена вдоль оси стержня сверху вниз от конца A до конца B. o=30 ° C медь и сталь cm= = 106 кг с повышением температуры! см *
коэффициент линейного температурного расширения Чжан АС=125-10-7, ам=165 * ю л, справа (рис. 52, а). Тот факт Штанга поддержки выбирает вверх и показывает RA и P b, которому состояние статики водит к Пара & Фигура. 52. РА+р = р. Чтобы лучше понять происходящую деформацию, предположим,
что нижний конец стержня свободен, а опора отсутствует (рис. 52, б). Это предположение Людмила Фирмаль
не меняет поведения конструкции, если движение этого конца равно нулю, а действие опоры учитывается наличием реакции этой опоры, которая добавляется к нижнему концу. Заметим, что статически определимый стержень, полученный отбрасыванием фиксированного «экстра» (для ряда уравнений равновесия), может выбрать только другую базовую систему, отбрасывая опору,
названную выше основной системой статически неопределенных структур (рис. 52, б). Основная система должна быть. И, конечно, помимо силы Р, есть еще и реакция этой верхней опоры утилизации. Базовая система, нагруженная всеми нагрузками и реакциями всех опор, полностью эквивалентна статически неопределенной структуре, к которой она выведена, если выполняется уравнение
- совместимости деформаций. Эти уравнения основаны на ограничениях, накладываемых на деформации опорой статически неопределенных систем. Решение связи с уравнением равновесия определяет величину всех неизвестных. В нашем случае условие совместимости состоит в том, что удлинение стержня от повышения температуры (свободный нижний конец) и его верхнее удлинение от силы Р должны быть численно равны. Укорочение стержня силой Р: Или ^Как±2^ам+ » Р1, 2EcF — £ 2 cf’R! Считанные секунды +2ECF2Ecf L1^£m J ’ отсюда находим реакцию P, из состояния статики и RA. Обе
реакции вызваны действием температуры, первый компонент вызван мощностью WG и мощностью WG, а затем проблема решается отдельно, изменяя порядок и мощность WG. Реакция от силы Р направлена вверх, от действия температуры реакция опоры В и опоры а-вниз(минус в Формуле РА). Таким образом, весь стержень сжимается температурной реакцией, далее верхняя часть растягивается, а нижняя часть сжимается силой: П Поэтому обозначим знак растягивающего напряжения и сжатия-и получим: =200-580= — 380кг / слс2 10E§ 25] пример 93 Д
ля верхней части и поперечного сечения ——- «п-ГЛТ!——— 580= — 680 кг) см* Д+к^-J20 Людмила Фирмаль
может Для секций в нижней части. При решении задачи необходимо обратить внимание на то, что удобно преобразовывать формулы для включения больших (E) или малых (a) соотношений. P R I m EP12. Стержень затягивается на верхней кромке и не доходит до нижней опоры в количестве D/o=1,25 ltlt; верхняя часть медного сердечника, длина / m=1,6 м, площадь GM=10cm2\нижняя часть-стальная, квадрат Fc=20Cu2, длина / s=0,8 найти напряжение стальной и медной частей. Чтобы найти напряжение, мы определяем реакцию RA и P. равновесное состояние является: RA+R V = R- Условие совмес
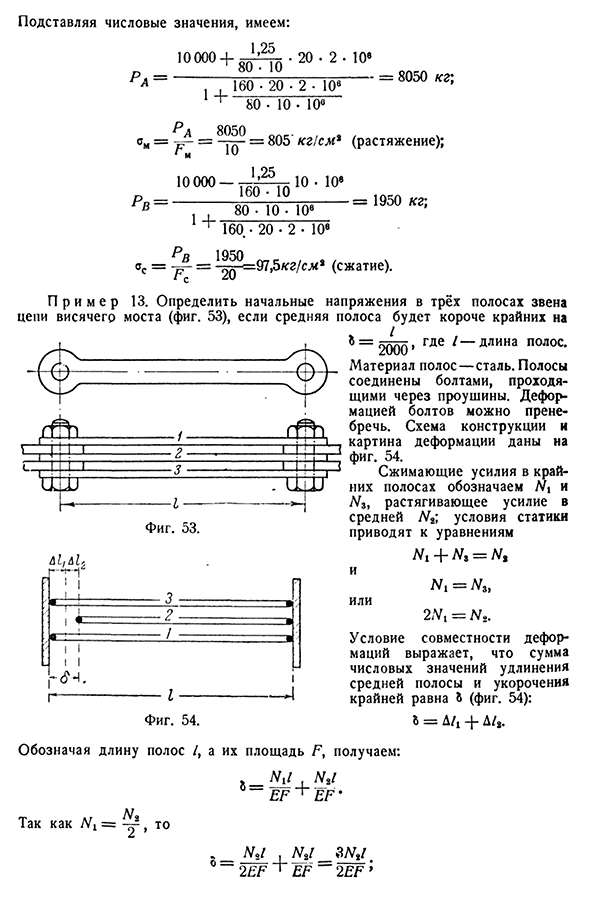
тимости деформации выражает идею о том, что разность между величиной удлинения в верхней части и укорочения в нижней равна зазору D / o: Д/Я~Д/С=Д/О Или ^А м Если вы замените RV на R-RA、: РА1», A1S_R1S Р. ECFC^ И так оно и есть. /mecfc11e IcEmFu Дж EcFc+Д / О И «94 статически неопределенная система вычислений(гл. (год Если присвоить число » | » -+8-й О-Р А160 * 20. 2. 10E1.+ 80 — 10 — 10E • 20 • 2 • 10″ =8050 кг\ Ом= = 805 ′ кг! Сантиметры * (растягивается); » ’» «» — » ’L’Y1″ — l f ’- F’=,, so. 10.10——- » 1950 1 + 1 6 0 я не уверен.2 02. 10E AC= — p — =^~L=97, 5k2 / C. ms (сжатие). П р и М Е Р13. Определите начальное напряжение трех полос звена цепи подвесного моста(рис. 53)Если средней полосе короче, чем крайняя я Или Ф, ГГ, 1 ноября. ———-
——3 ——————— 1а——————- 2 ————————— ■ / ■ 1t———————, чтобы—-1—— 1——————— / — Нет, — ответил он. ■в Z——1, 1 1 Ф■ ■ / /1 1 1 1-1. ■ Зет » Один. Показывает длину полосы и ее площадь 8= = £ф+ф’ D= = ~так что тогда S=2566″G d E1 длина полосы. Материал прокладки сталь. Прокладка соединена болтами через отверстию. Деформацию болта можно проигнорировать. Схемы схемы и деформации конструкции показаны на схеме. 54. Сила сжатия крайнего диапазона указывает на растягивающее усилие M и N3, промежуточное W8. Н = lgz по,2Nt = Н2. Совместимость по умолчанию-ее общее количество Условие M указывает, что удлинение средней полосы и крайнее укорочение равны&. 54): 5=D / 2″ Получать: / V2Z ФВ O=§ 26] концепция расчета допустимой нагрузки 95 Но Внешний Ноль. 1. Напряжение в средней полосе составляет » — =23 22000-6 6 7K g! м(растяжка). Экстремальные группы давлени
я в два раза меньше, а п р и М Е С14. Внутри чугунной трубы проходит стальной болт диаметром 30 мм. 55), внутренний диаметр равен =32мм, ДТ=62мм. Гайка болта завинчивается так, что головка и шайба соприкасаются с концом трубы, но Болт еще не натянут. Длина трубы/=500 м, F c=2-1 0e кг! cm\£h=1, 2-10E кг! смкак долго нужно вкручивать гайку в болт, чтобы вызвать натяжение P-12g? Что такое напряжение в чугунной трубе? Завинчивание гайки вызовет реакцию между концом стиральной машины и трубкой. Эти реакции сжимают трубы и растягивают болты; они должны быть равны
12 тоннам. Укорочение трубки плюс удлинение болта и Поперечное сечение трубки составляет FT=(d — df)= — J(6,2 с-3,2 с)=22,1 см. Площадь поперечного сечения Болта Гайки нуждаются в движении ECF6^E4FT EcF6[l^E4FT\— 12 000 • 500 G., 2•10E * 7,071 2 * 10E•7,07 [+1,2•10E * 22,1 J^O, M M]
Смотрите также:

