Пример построения однофакторной регрессионной модели
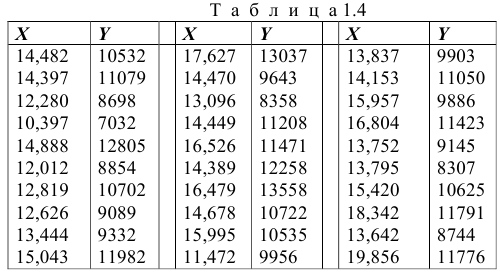
Исследуем зависимость выпуска валовой продукции на одного среднегодового работника сельского хозяйства (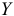 , день, ед.) от фондовооруженности одного работника, занятого в сельскохозяйственном производстве (
, день, ед.) от фондовооруженности одного работника, занятого в сельскохозяйственном производстве (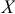 , тыс. ден. ед. на человека), по данным 30 колхозов Республики Беларусь (табл. 1.4). Фондовооруженность выбрана в качестве факторного признака исходя из экономических соображений. Спрогнозируем выпуск валовой продукции при фондовооруженности
, тыс. ден. ед. на человека), по данным 30 колхозов Республики Беларусь (табл. 1.4). Фондовооруженность выбрана в качестве факторного признака исходя из экономических соображений. Спрогнозируем выпуск валовой продукции при фондовооруженности 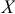 = 20тыс. ден.ед., построим доверительный интервал для данного прогноза.
= 20тыс. ден.ед., построим доверительный интервал для данного прогноза.
Из расположения точек
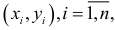
на корреляционном поле предположим линейную связь между переменными. Эмпирическую прямую регрессии 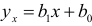 построим, используя ПЭВМ (программа АРМС).
построим, используя ПЭВМ (программа АРМС).
Оцениваемую линейную корреляционную связь можно представить в виде эмпирического уравнения регрессии:
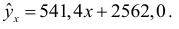
Проверим значимость коэффициента регрессии 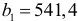 . Для этого выдвинем гипотезу
. Для этого выдвинем гипотезу 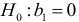 состоящую в том, что переменная
состоящую в том, что переменная 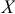 не оказывает существенного влияния на зависимую переменную
не оказывает существенного влияния на зависимую переменную 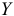 , против альтернативной гипотезы
, против альтернативной гипотезы 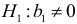 . Статистика
. Статистика
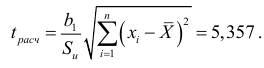
По таблице 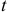 -распределения для уровня значимости
-распределения для уровня значимости 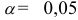 и
и 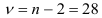 степеней свободы находим критическое значение статистики:
степеней свободы находим критическое значение статистики: 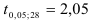 (при двусторонней критической области). Так как
(при двусторонней критической области). Так как 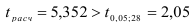 , то фондовооруженность, переменная
, то фондовооруженность, переменная 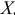 , оказывает существенное влияние на валовую продукцию, переменная
, оказывает существенное влияние на валовую продукцию, переменная 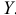 .
.
В рассматриваемом примере коэффициент регрессии показывает, что валовая продукция в среднем возрастает на 541,4 ден. ед., если фондовооруженность увеличивается на 1 тыс. ден. ед. . Коэффициент регрессии отражает влияние изменения уровня фондовооруженности на объем выпуска валовой продукции.
Оценим интенсивность связи между фондовооруженностью и объемом выпуска валовой продукции, используя коэффициент корреляции. Так как коэффициент линейной корреляции 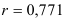 , то между изучаемыми факторами существует тесная корреляционная связь.
, то между изучаемыми факторами существует тесная корреляционная связь.
Проверим значимость коэффициента корреляции, выдвинув нулевую гипотезу 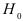 : различие между
: различие между 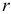 и
и 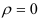 незначимо, и альтернативную гипотезу
незначимо, и альтернативную гипотезу 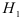 : различие между
: различие между 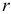 и
и 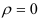 значимо. Вычисленную по результатам выборки статистику
значимо. Вычисленную по результатам выборки статистику
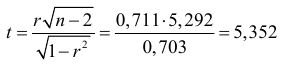
сравним с критическим значением, определенным по таблице распределения Стьюдента при заданном уровне значимости 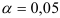 и
и 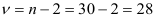 степенях свободы:
степенях свободы:  (воспользовались двусторонней критической областью). Так как
(воспользовались двусторонней критической областью). Так как 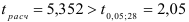 , то гипотеза
, то гипотеза 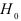 отвергается на уровне значимости 0,05. С вероятностью
отвергается на уровне значимости 0,05. С вероятностью 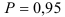 можно утверждать, что между фондовооруженностью и объемом выпуска валовой продукции существует тесная корреляционная зависимость.
можно утверждать, что между фондовооруженностью и объемом выпуска валовой продукции существует тесная корреляционная зависимость.
Исследуем адекватность построенной однофакторной модели изучаемому экономическому процессу. Вычисленное по результатам выборки 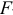 -отношение равно
-отношение равно 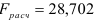 . Сравниваем его с квантилем табличного
. Сравниваем его с квантилем табличного 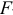 -распределения, определенного при уровне значимости
-распределения, определенного при уровне значимости 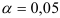 и
и 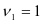 и
и 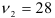 степенях свободы:
степенях свободы: 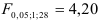 . Так как
. Так как 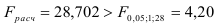 , то уравнение регрессии с вероятностью
, то уравнение регрессии с вероятностью 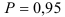 признается значимым.
признается значимым.
Используем остатки в качестве характеристики степени согласованности расчетных значений регрессии и наблюдаемых значений переменной 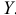 .
.
Подставив в полученное уравнение регрессии значения 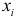 из табл. 2.18, вычислим значения регрессии
из табл. 2.18, вычислим значения регрессии 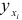 и остатки
и остатки 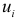 .
.
Стандартная ошибка остатков рассматривается как стандартная ошибка оценки регрессии в связи с интерпретацией возмущающей переменной 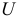 как результата ошибки спецификации функции регрессии. Находим несмещенную оценку дисперсии возмущающих воздействий
как результата ошибки спецификации функции регрессии. Находим несмещенную оценку дисперсии возмущающих воздействий 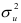 :
:
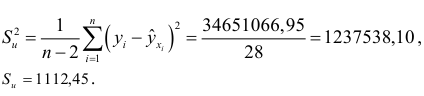
Из значений остатков следует, что необходимо прежде всего проанализировать деятельность колхозов с номерами 26, 4, 13, 23, 29, 30, 5, 16, 17 и 7, показатели которых отличаются большими отклонениями в ту и другую стороны от значений, предсказанных по уравнению регрессии. В колхозах, для которых обнаружены отрицательные отклонения фактических значений от расчетных, следовало бы уделить особое внимание экономической и организационной работе.
Среднеабсолютная процентная ошибка, вычисленная для данных рассматриваемого примера,
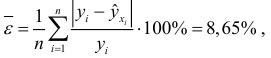
что свидетельствует о высокой точности построенного уравнения регрессии.
Для определения того, какая часть полного рассеяния значений  обусловлена изменчивостью переменной
обусловлена изменчивостью переменной  , вычислим коэффициент детерминации. Так как
, вычислим коэффициент детерминации. Так как 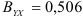 , делаем вывод, что только 50,6% общей дисперсии объема выпуска валовой продукции в рассматриваемых колхозах обусловлено вариацией фондовооруженности. Это значит, что в регрессионную модель нужно вводить дополнительные факторы, оказывающие влияние на объем выпуска валовой продукции. Коэффициент неопределенности
, делаем вывод, что только 50,6% общей дисперсии объема выпуска валовой продукции в рассматриваемых колхозах обусловлено вариацией фондовооруженности. Это значит, что в регрессионную модель нужно вводить дополнительные факторы, оказывающие влияние на объем выпуска валовой продукции. Коэффициент неопределенности 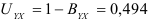 , или 49,4%. Следовательно, 49,4% общей дисперсии нельзя объяснить зависимостью объема выпуска валовой продукции от фондовооруженности.
, или 49,4%. Следовательно, 49,4% общей дисперсии нельзя объяснить зависимостью объема выпуска валовой продукции от фондовооруженности.
Таким образом, из анализа всех показателей адекватности модели следует, что уравнение регрессии статистически значимо, но в построенную модель следует ввести еще ряд факторов, влияющих на объем выпуска валовой продукции.
Подставив в построенное эмпирическое уравнение регрессии значение фондовооруженности 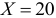 найдем прогнозное значение объема выпуска валовой продукции
найдем прогнозное значение объема выпуска валовой продукции 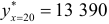 ден.ед. Соответствующий доверительный интервал буде иметь вид:
ден.ед. Соответствующий доверительный интервал буде иметь вид:
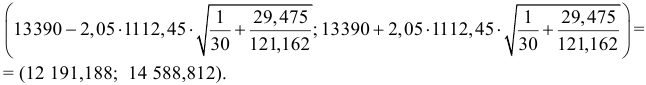
Следовательно, средний объем выпуска валовой продукции при фондовооруженности 20 ден. ед. будет находиться в интервале (12 191,188; 14 588,812).
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:

