Задача №91.
Пример имеет своим прототипом схему подъема мачтовых опор ЛЭП с помощью тягачей (рис. 3.55).
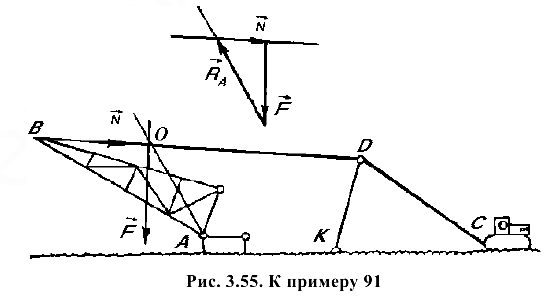
Рассмотрим эту схему.
Мачта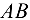 
, лежащая возле заранее подготовленного фундамента, соединяется с ним шарниром 
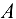. Затем с помощью канатной тяги 
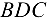она поднимается до вертикального положения. При этом вспомогательная штанга 
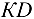облегчает работу в начальной стадии подъема, отводя направление тяги несколько вверх. Здесь осуществляется типичный случай равновесия трех сил, расположенных в одной плоскости (в данном случае — в вертикальной). Эти силы сходятся в некоторой точке 
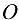, определяемой пересечением каната с линией силы тяжести мачты. Искомая реакция также выходит па эту точку.
Решение:
Графическое решение задачи состоит в том, что, считая силу тяжести мачты, а также ее угол и угол каната с горизонтом известными, необходимо построить на векторе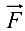 
в определенном масштабе замкнутый силовой треугольник при точке 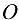, которую выгодно вынести в сторону от основного чертежа. Стороны треугольника должны быть строго параллельны направлениям искомых сил, тогда величины этих сил будут найдены прямым измерением сторон треугольника в миллиметрах и умножением их на выбранный масштаб.
Аналитическое решение задачи состоит в использовании уравнений равновесия, система которых для произвольных сил на плоскости имеет вид
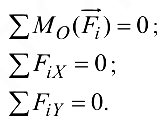
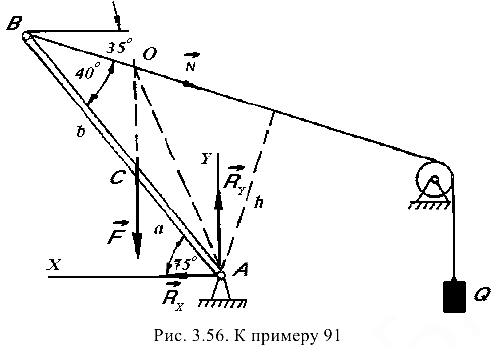
Решение показано на несколько видоизмененной схеме (рис. 3.56).
Пусть мачта 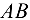в данный момент подъема составляет с горизонтом угол, равный 75°, а тяга 
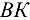наклонена к горизонту под углом 35°. Угол между мачтой и канатом получается равным 40°. Пусть центр тяжести 
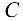делит длину мачты па отрезки
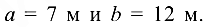
Вес мачты
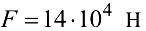
(масса — 14 т). Требуется определить силу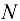 
натяжения каната и реакцию опоры 
.
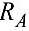Решение:
За начало координат принять шарнир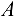 
, направив ось 
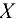в сторону наклона мачты, а ось 
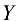— вверх. Тогда уравнение моментов примет вид
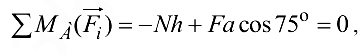
где
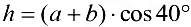
(плечо силы 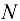относительно центра моментов 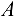). Отсюда
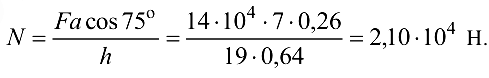
Уравнения проекций сил на координатные оси
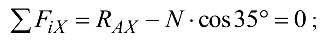
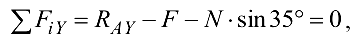
откуда
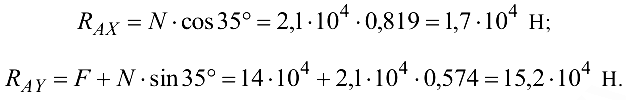
Положительные значения реакций указывают на то, что их направления на чертеже выбраны верно (не забудьте, что ось 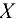здесь направлена влево!).
Полная реакция шарнира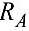
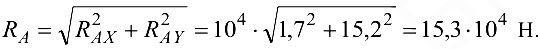
Её угол с горизонтом легко определяется по тангенсу. Для проверки решения нужно убедиться, что линия действия реакции 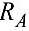действительно выходит на точку пересечения линий сил 
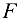и .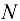
Ответ:
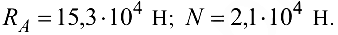
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:
