Пример №27.
Рассмотрим такую ЗЛП:
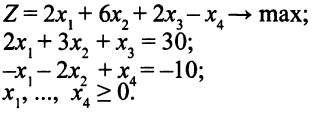
Математическая модель двойственной задачи:
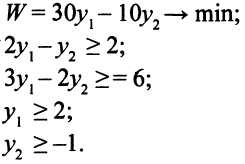
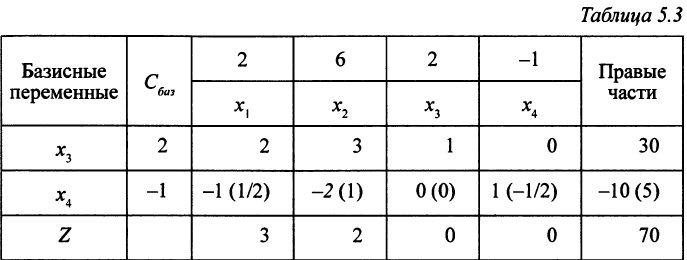
Составим первую симплекс-таблицу (табл. 5.3).
Вектор
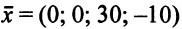
недопустим, так как
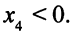
Но вектор
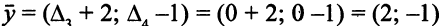
допустимое решение двойственной задачи.
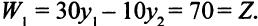
Перейдем к вектору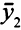 
, на котором целевая функция 
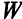уменьшится.
Сначала выберем уравнение, в котором заменяется базисная переменная. Условимся уменьшать целевую функцию 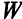, выбирая правую часть и соответствующий опорный элемент отрицательными.
Имеется только одна отрицательная правая часть (во втором уравнении), поэтому замену переменной проведем во втором уравнении.
Отметим, что если бы в левой части второго уравнения все коэффициенты были неотрицательны, то задача (5.26) не имела бы ни одного допустимого решения, ведь уравнение вида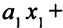 
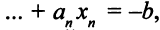, где
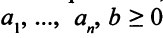
не имеет неотрицательных решений.
Есть две возможности выбрать новую базисную переменную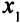: или 
или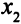 
. Сделаем выбор, исходя из требования неотрицательности всех оценок 
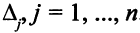. По формуле пересчета
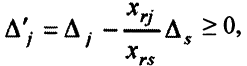
где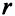 
— номер уравнения, в котором заменяется базисная переменная; 
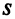— номер новой базисной переменной.
Так как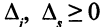 
и было условлено, что 
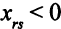, то наверняка 
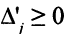, когда 
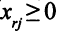. Если же 
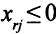, то условие (5.24) можно записать в виде
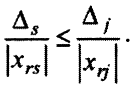
Итак, отношение
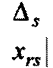
должно быть минимальным из всех
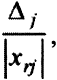
отношений, таких, что
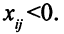
В нашем случае имеем:
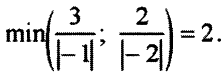
Новой базисной
переменной становится переменная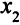 
. Построим табл. 5.4.
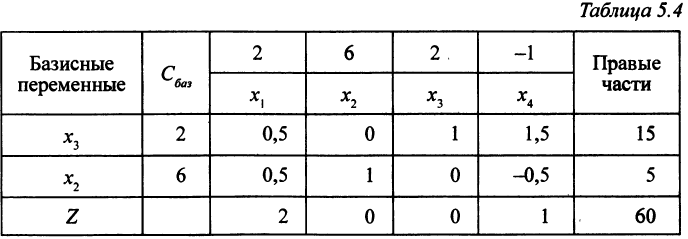
Вектор
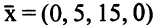
допустимое и оптимальное решение задачи (5.26). Вектор
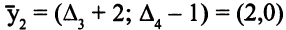
допустимое и оптимальное решение двойственной задачи,
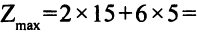
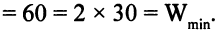
Эта задача взята со страницы решения задач по предмету «линейное программирование»:
Решение задач по линейному программированию
Возможно эти страницы вам будут полезны:
