Пример №24.
Рассмотрим такую ЗЛП:
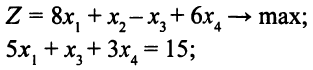
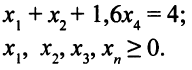
Приведем математическую модель двойственной задачи.
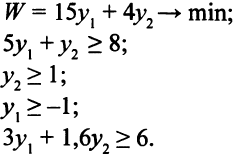
Запишем решение этой задачи в симплекс-таблицах (табл. 5.2).
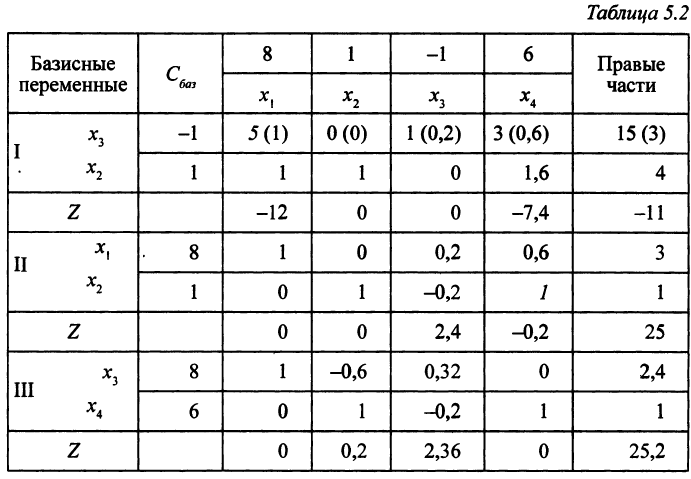
Оптимальное решение:
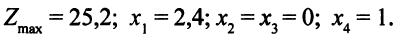
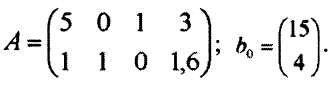
На первой итерации базисные переменные — это переменные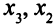 
. Значит, 
;
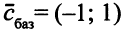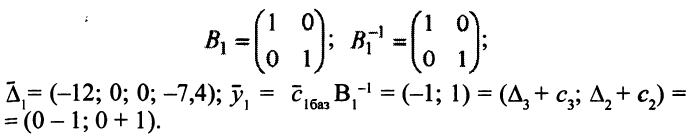
Так как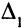 
и 
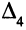меньше нуля, первое и четвертое ограничения двойственной задачи не удовлетворяются для данных значений 
.
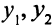На второй итерации базисные переменные — это переменные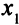 
и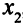 
, тогда
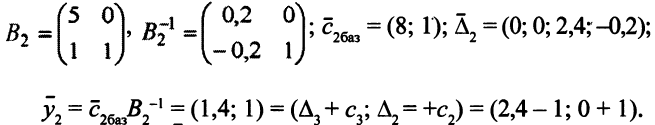
На векторе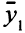 
= (1,4; 1) не удовлетворяется четвертое ограничение двойственной задачи, так как 
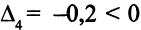. В части III табл. 5.2 записано оптимальное решение. Имеем:
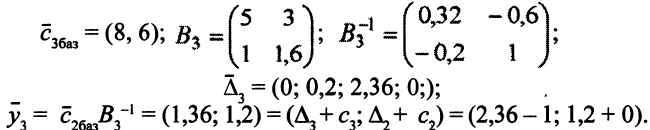
Все оценки неотрицательны,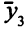 
— оптимальное решение двойственной задачи.
Эта задача взята со страницы решения задач по предмету «линейное программирование»:
Решение задач по линейному программированию
Возможно эти страницы вам будут полезны:
