Приложение полученных формул к элементарным функциям

Оглавление:

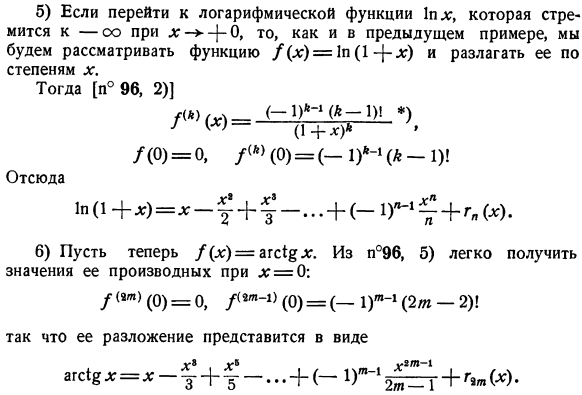
Приложение полученных формул к элементарным функциям

Приложение полученных формул к элементарным функциям. Формула Тейлора выглядит более простой для г0 0 = 0 *)： ПХ) = ф(0)+ ^ ХХ * + … х » + рН(х).(18） Этот частный случай всегда можно уменьшить, используя x-x9 в качестве новой независимой переменной. Рассмотрим несколько конкретных разложений по этой формуле элементарных функций. 1) f (x)= e *;и f(x) (g;)= r * любой a = 1, 2,3,..И [96, 3)]. в этом случае/(0)= 1, f * * >(0)= 1, поэтому по формуле (18)、 gDG = 1 + T + 2T±+ 5 + g’M2) если f (DG)= 81PX, f(A) (A;)= 3!^ ^ + K•[N°96, 4）] Что?! /(0)= 0,/ {9м)(0)= ы! N m = 0、 (0)= 81N [m = (I) » −1(m = 1, 2, 3,…это не так.

В этом случае сама функция (при m<0) или ее производная (при n> m, начиная с определенного порядка) возрастает до бесконечности. Людмила Фирмаль

Итак, если поставить формулу (18) n = 2 / n、 * 1 y-1 / 71— 1 $ 1nx = ДГ СГ + 5г•• * +(о» * *(2Т-1)!)Г * т 3) аналогично, f ( * ) = cos.* [N°96, 4）] / Л> ()= соѕ( + л.|-); /(0)= 1,/• «> » =(-1Л ( * » * ~ !) (0)= 0 (m = 1,2,3,…это не так. Итак(если взять η= 2 / π / −1）： Да! * 4 * 2 SOPL = 1-2G + 4G + 1) I ’(2-й)| + G5’l +>4) здесь рассмотрим функцию возведения в степень xm, где m не является ни натуральным числом, ни a zero. In в

Поэтому здесь нельзя брать hc0 = 0. G0 = 1, то есть мы разлагаем x * 11 со степенью x-11. Продолжите с x и разверните функцию (1 -) -) m в степени x. Как вы знаете[n°96, 1）]、 / <>()= М(М-1)…(м-к + 1) (1 + х) м〜\ Как это Ф(0)= 1,ф <>(0)= Ф(М-1)… {м-к + 1). Формат расширения (1 + xT = 1 + mx + * + … + М (М-1)…(М-L + 1), _ л. Т TGTGGn ^ + Р «(■*）• 5).

Однако, как уже упоминалось, x-1 может быть введена в качестве новой переменной. Людмила Фирмаль

Если вы перейдете к логарифмической функции\ nx, она имеет тенденцию быть-oo как x > 0, и, как в предыдущем примере, подумайте о функции, которая разрушается силой x. Затем [n°96, 2）] / * ’（） /(0)= 0,/ <а>(0)=(-я) ’ 1 {к-1)! 1Н.（1 + *）= *-^ + ^ -… +(1Г1^ +гя (.*）、 (А-Д)| Отсюда 6) где f (x)= ags ^ n;. предполагается, что из N°96 легко получить значение производной при 5) x = 0： / * «>（0）= 0、（0）=（-я)™-1(2М-2)! Так что разложение появляется в виде Т-1 ЛТ-1 2Т-1 \Γ} м(х).

Разложение произвольной функции.	Приближенные формулы. Примеры.
Другая форма дополнительного члена.	Условие постоянства функции.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.