Оглавление:
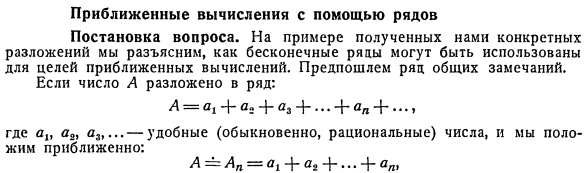



Приближенные вычисления с помощью рядов. Постановка вопроса
Приближенные вычисления с помощью рядов. Постановка вопроса. Описывает, как использовать бесконечный ряд для приближенных вычислений с использованием конкретного полученного разложения. Давайте предварим некоторые общие замечания. Если номер находится в преемственности: А = С,+ а+ Д3 + Ай + •• Где a, a2, al,… полезное (обычно разумное) число, и приблизительно Л = в = 4-й топор• * * + на Модификация для отбрасывания всех остальных терминов выражается в виде остатка к = Ал + 1 + ВЯ + 2 4 -… если n достаточно велико, то эта ошибка будет сколь угодно мала, и An будет воспроизводить A с заданной точностью заранее. Интересует возможность просто оценить весь остальной ад.
Это позволяет вовремя остановиться при вычислении последовательных частичных сумм, когда вы уже получили аппроксимацию требуемой точности. Людмила Фирмаль
- Если окажется, что рассматриваемый ряд чередуется, и к тому же абсолютное значение члена монотонно уменьшается («тип Лейбница»), то остальные, как мы видели в[Г244, Примечания], будут иметь знак первого члена, а абсолютное значение будет меньше. Такая оценка в смысле простоты оставляет желать лучшего. Для положительных серий ситуация несколько сложнее. Затем они обычно пытаются найти положительный ряд с большим членом. Ноль ноль
- Краткое резюме: IX.%^и в качестве оценки Я Остальные вывода занимает оставшиеся в этой новой серии: ай ^ ай. Например Два м = п -1 И Один И т \ л! м = н—\ м •я + 1 У. н \& Один (я+) т-н Один н Для числа [мы фактически использовали эту оценку при вычислении числа e в N°49]. Как правило, вы найдете десятичное приближение числа A}, но члены ряда не могут быть выражены в виде десятичных знаков. Если вы преобразуете их в базу 10, округление вызовет новую ошибку, но это также следует учитывать.
Наконец, заметим, что не все ряды с числом A, представляющим интерес, подходят для вычисления этого числа (даже если термин прост, а остальное легко оценить). Людмила Фирмаль
- Задача состоит в скорости сходимости, то есть скорости приближения к числу L частных сумм. Берет ряд, например[ссылки n°255, (20)и n* 256、(22)] 1-3 + 3-Т + …И+ Дайте численное разложение и 1n 2, соответственно. Они сходятся очень Медленно, чтобы с высокой точностью найти приблизительные значения этих цифр, с их помощью нужно суммировать огромное количество членов. Ниже мы очень точно находим 10-шестнадцатеричное приближение упомянутого числа, без конкретных трупов, используя более подходящий ряд.
Смотрите также:
Решение задач по математическому анализу
| Биномиальный ряд. | Вычисление числа пи. |
| Замечание об исследовании дополнительного члена. | Вычисление логарифмов. |
Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.

